Entanglement in the Quantum Phase Transition of the Half-Integer Spin One-Dimensional Heisenberg Model ()
Received 11 November 2015; accepted 26 December 2015; published 29 December 2015

1. Introduction
The study of entanglement in quantum spin chains has been subject of intense research recently. In this field of knowledge, theory of quantum information and condensed matter theory intertwine. In special, the study of properties of entanglement in systems of many particles and analysis of its behavior near quantum phase transition deserve much attention [1] [2] . In this work, we deal entanglement of low-lying magnetic excitations in the spin-1/2 one-dimensional Heisenberg model (HM). It is well known that one-half spin chains are different from integer spin chains due to the opening of a gap in the spectrum, where integer spin chains present a gap in the spectrum known as the Haldane gap [3] [4] . It is also known that there is an absence of this gap in the half-integer spin Heisenberg chains according to the Lieb, Schultz and Mattis theorem [5] . Besides, the low-ly- ing excitations are different for integer and half-integer spin chains. While in the integer spin chains the excitations are magnons, in the half-integer spin chains, the excitations are spinons that are particles without charge but spin one-half. It is very important to understand the entanglement of these quasi-particles in neighborhood of the quantum phase transition which is well known to be dominated by strong quantum fluctuations.
One-half spin chains present a quantum phase transition with the anisotropy parameter . In the range
. In the range  the system does not present gap in the spectrum. When
the system does not present gap in the spectrum. When 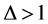 and
and , there is an opening of a gap in the spectrum. It is important to know the influence of these quantum phase transitions on the entanglement.
, there is an opening of a gap in the spectrum. It is important to know the influence of these quantum phase transitions on the entanglement.
The spin one-half Heisenberg model was solved exactly for the first time by Bethe in 1931; the solution was known as the Bethe’ ansatz [6] . In reality the initial solution proposed by Bethe is nominated as coordinates of the Bethe’s ansatz. However, the Bethe’s ansatz suffered modifications among the years and today uses a version modified by the initial Bethe’s ansatz nominated as the algebraic Bethe’s ansatz.
The quantum spin-1/2 (HM) was much studied extensively in the literature using the Jordan-Wigner transformation and Abelian and non-Abelian bosonization. The thermodynamic properties of this model were studied by Klümper in Ref. [7] [8] . The dynamics properties such as spin and thermal transport were also extensively studied [9] -[14] .
For the integer spin Heisenberg chains, the thermodynamics properties and dynamics such as spin transport were much studied in the literature using different methods. The non-linear sigma model was used by Haldane [3] [4] ; he verified that integer spin chains are different from half-integer spin by opening a gap in the spectrum until by the use of spin wave approximations [15] -[18] , Schwinger boson theory [19] -[23] and so on.
In general, entanglement is a property at the heart of quantum mechanics [24] , which was first brought to the intriguing questions posed by Einstein, Podolsky and Rosen [25] . Entanglement is defined in terms of some kinds of instantaneous interaction, contrary to the relativistic principle that all interaction is possible only at a velocity less than that of light [26] . The entanglement in the quantum critical phenomena in one-dimensional spin-1/2 XX and XY models were studied by Vidal et al. [27] , in non-critical and critical regimes. He calculated the entropy for a block of L contiguous spins. The entanglement for 1D spin-1/2 XY model was calculated for a lattice with N sites in transverse field by [28] -[30] .
The aim of this paper is to verify the influence of quantum phase transition on entanglement of the quantum one-half spin Heisenberg model. This work is divided in the following way. In Section 2, we discuss the properties of the model. In Section 3, we develop the analytical tools to calculate the entanglement of the system. In Section 4 we present the analytical results, and in the last section, Section 5, we present the conclusions and the final remarks.
2. The Model
The model is defined by the following Hamiltonian
 (1)
(1)
with periodic boundary conditions on a chain of length L. When  the system is an isotropic Heisenberg antiferromagnetic (AFM). For
the system is an isotropic Heisenberg antiferromagnetic (AFM). For , the system reduces to the isotropic Heisenberg ferromagnetic (FM). The
, the system reduces to the isotropic Heisenberg ferromagnetic (FM). The 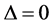 correspond to the XY model. The anisotropy parameter is conveniently parameterized by
correspond to the XY model. The anisotropy parameter is conveniently parameterized by , where
, where . We restrict to the critical regime
. We restrict to the critical regime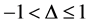 , where the system displays correlation functions algebraically decaying to zero temperature [9] . For
, where the system displays correlation functions algebraically decaying to zero temperature [9] . For![]() , easy axis, the system is Ising like which is the simplest quantum lattice system to exhibit a quantum phase transition [31] . The dependence of the ground state with
, easy axis, the system is Ising like which is the simplest quantum lattice system to exhibit a quantum phase transition [31] . The dependence of the ground state with ![]() is quite complicated. However, it is possible to investigate the
is quite complicated. However, it is possible to investigate the ![]() limit exactly [28] .
limit exactly [28] .
3. Algebraic Bethe’s Ansatz
We search for a pseudo-vacuum state ![]() that is a simple eigenstate of the diagonal operator valued with entries A and D of the monodromy matrix
that is a simple eigenstate of the diagonal operator valued with entries A and D of the monodromy matrix![]() , where
, where![]() . The lower-left entry C of the monodromy matrix applied to
. The lower-left entry C of the monodromy matrix applied to ![]() yields zero, the upper-right of the entry B yields new non vanishing states. Hence C and B play the role of annihilation and creation operators.
yields zero, the upper-right of the entry B yields new non vanishing states. Hence C and B play the role of annihilation and creation operators.
The reference state is given by
![]() (2)
(2)
where ![]() are the local states. The monodromy matrix
are the local states. The monodromy matrix ![]() applied to
applied to ![]() yields an upper triangular
yields an upper triangular ![]() matrix of states
matrix of states
![]() (3)
(3)
or explicitly
![]() (4)
(4)
Therefore, ![]() is an eigenstate of
is an eigenstate of![]() . We intend to use the operators B as creation operators for excitations, i.e. we demand that the new state
. We intend to use the operators B as creation operators for excitations, i.e. we demand that the new state ![]() (one-particle state) be an eigenstate of
(one-particle state) be an eigenstate of![]() . The algebra for exchange
. The algebra for exchange ![]() with
with ![]() and
and ![]() can be obtained from the Yang-Baxter equation
can be obtained from the Yang-Baxter equation
![]() (5)
(5)
We have that
![]() (6)
(6)
where![]() ,
,![]() . For any N-particle state, we look at the following state
. For any N-particle state, we look at the following state
![]() (7)
(7)
where the numbers ![]() are Bethe ansatz roots of
are Bethe ansatz roots of
![]() (8)
(8)
for ![]() and
and ![]() is the eigenvalue.
is the eigenvalue.
The Bethe’s ansatz equation above is the basis of an efficient analytical and numerical treatment of the thermodynamics of the Heisenberg chain. There are, however, variants in form of integral equations that are somewhat more convenient for the analysis in the case where the external magnetic fields h close to![]() . The alternative integral expression for the eigenvalues
. The alternative integral expression for the eigenvalues ![]() reads
reads
![]() (9)
(9)
where
![]() (10)
(10)
where![]() . The ground state energy
. The ground state energy ![]() is given in [7] and
is given in [7] and![]() ,
, ![]() are complex-valued functions with integration paths along the real axis. These functions are determined from the following set of non-linear integral equations
are complex-valued functions with integration paths along the real axis. These functions are determined from the following set of non-linear integral equations
![]() (11)
(11)
where ![]() and
and
![]() (12)
(12)
the symbol ![]() denotes the convolution product
denotes the convolution product ![]() and
and ![]() is defined by
is defined by
![]() (13)
(13)
where the Equation (11) can be simplified in the limit![]() .
.
4. Entanglement and Quantum Phase Transitions
A measure of the degree of entanglement of a quantum state is the von Neumann entanglement entropy. Considering a partition of a physical system ![]() into two disjoint subsystems that we will label by A and B where
into two disjoint subsystems that we will label by A and B where ![]() and
and![]() . The Hibert space of states on
. The Hibert space of states on ![]() is
is![]() . Let
. Let ![]() be a pure quantum state of the system on
be a pure quantum state of the system on![]() , as such it can be decomposed as [1] [2]
, as such it can be decomposed as [1] [2]
![]() (14)
(14)
where ![]() and
and ![]() are orthonormal basis states of
are orthonormal basis states of ![]() and
and![]() , respectively, and
, respectively, and ![]() are the
are the
matrix elements of an (in general) rectangular matrix![]() . Using the singular-value-decomposition theorem, we can write
. Using the singular-value-decomposition theorem, we can write![]() , where
, where ![]() is a unitary matrix, and
is a unitary matrix, and ![]() is a diagonal matrix
is a diagonal matrix![]() . Then
. Then
after going to the new bases, ![]() and
and![]() , we find the Schmidt decomposition of the state vector
, we find the Schmidt decomposition of the state vector![]() ,
,
![]() (15)
(15)
where![]() , with
, with ![]() and
and ![]() being the dimensions of the Hilbert spaces
being the dimensions of the Hilbert spaces ![]() and
and![]() . If the
. If the
state vector ![]() is normalized to unity,
is normalized to unity, ![]() , then the set of complex numbers
, then the set of complex numbers ![]() must satisfy the sum rule
must satisfy the sum rule
![]() (16)
(16)
The model Equation (1) has the unique ground state![]() . In the ground state, the entropy for the whole system vanishes but the entropy of a sub-system can be positive. We treat the whole chain as a binary system
. In the ground state, the entropy for the whole system vanishes but the entropy of a sub-system can be positive. We treat the whole chain as a binary system![]() , where we denote the block of L neighbouring spins by sub-system A and the rest of the chain by sub-system B [29] . The density matrix of the pure state
, where we denote the block of L neighbouring spins by sub-system A and the rest of the chain by sub-system B [29] . The density matrix of the pure state ![]() of the total system
of the total system ![]() is
is
![]() (17)
(17)
We can define the reduced density matrix for subsystem A to be the partial trace of ![]() over the degrees of freedom in B as
over the degrees of freedom in B as
![]() (18)
(18)
and similarly for the reduced density matrix![]() .
.
The von Neumann entanglement entropy ![]() for subsystem A, when the total system is in state
for subsystem A, when the total system is in state![]() , is defined to be the entropy of the reduced density matrix,
, is defined to be the entropy of the reduced density matrix,
![]() (19)
(19)
It also follows that the von Neumann entanglement entropy can be written as
![]() (20)
(20)
i.e. the entanglement entropy is symmetric in the two (entangled) subsystems. This symmetry property is a consequence of our assumption that the total system ![]() is in a pure state
is in a pure state![]() .
.
In the quantum field theory the Gibs’ density matrix of the system is![]() , where
, where ![]() is the quantum Hamiltonian. The partition function is [32] [33]
is the quantum Hamiltonian. The partition function is [32] [33]
![]() (21)
(21)
It is well known that in the critical regime the entropy diverges logarithmically with the size of a block of L spins [27] [33] [34] . As derived in Ref. [35] , in ![]() conformal field theory the entropy of a subregion of length L reads
conformal field theory the entropy of a subregion of length L reads
![]() (22)
(22)
with a coefficient given by the holomorphic and anti-holomorphic central charges c and ![]() of the theory.
of the theory.
5. Results and Discussion
In thermodynamic limit, we have [7]
![]() (23)
(23)
The integral expression for ![]() is given by Equation (9).
is given by Equation (9).
The Helmholtz free energy is
![]() (24)
(24)
where ![]() is the largest eigenvalue of the quantum transfer matrix [9] . The entropy is consequently given as
is the largest eigenvalue of the quantum transfer matrix [9] . The entropy is consequently given as
![]() (25)
(25)
At ![]() we must have
we must have ![]() as predicted by Nerst’s law. For high T we must have
as predicted by Nerst’s law. For high T we must have![]() . However for low temperature we must have S dominated by the quantum fluctuations near the quantum phase transition where the correlation length
. However for low temperature we must have S dominated by the quantum fluctuations near the quantum phase transition where the correlation length ![]() diverges in the quantum transition phase
diverges in the quantum transition phase![]() .
.
The von Neumann entropy provides a good quantifier for the entanglement in the thermodynamic limit which is also equivalent to the entanglement of distinguished particles. We can define the entanglement for a N number of particles as [1] [2]
![]() (26)
(26)
where![]() . Here
. Here ![]() means
means![]() . When
. When ![]() we have, in this case, the entropy of entanglement is simply the von Neumann entropy of the reduced matrix of one particle and do not have the factor
we have, in this case, the entropy of entanglement is simply the von Neumann entropy of the reduced matrix of one particle and do not have the factor![]() . We have that
. We have that
![]() (27)
(27)
In the limit![]() , the first term of the Equation (9) turns into [9]
, the first term of the Equation (9) turns into [9]
![]() (28)
(28)
a rather irrelevant term as it is linear in ![]() and
and![]() , therefore the second derivatives with respect to
, therefore the second derivatives with respect to ![]() and
and ![]() vanishes.
vanishes.
The functions ![]() and
and ![]() are given by Equation (11) and Equation (12). The summation in Equation (11) can be simplified in the limit
are given by Equation (11) and Equation (12). The summation in Equation (11) can be simplified in the limit ![]() as
as
![]() (29)
(29)
or
![]() (30)
(30)
where the first function is
![]() (31)
(31)
and the second function is given by
![]() (32)
(32)
![]() ,
, ![]() is given by [9]
is given by [9]
![]() (33)
(33)
From the Equation (9) we have finally
![]() (34)
(34)
therefore we obtain the entanglement in function of the ![]() parameter in the thermodynamic limit as
parameter in the thermodynamic limit as
![]() (35)
(35)
![]() , which is equivalent
, which is equivalent![]() , corresponds to the XY model. As we have
, corresponds to the XY model. As we have ![]() the entanglement is
the entanglement is![]() . In general the integral Equations (11) do not admit analytic solution [9]
. In general the integral Equations (11) do not admit analytic solution [9]
consequently we cannot solve the integral (35) directly. However an iterative procedure is conceivable to solve the Equation (11). Performing a saddle point integration we can find an expression for the entanglement in the low-temperature limit as
![]() (36)
(36)
where
![]() (37)
(37)
For ![]() we have
we have
![]() (38)
(38)
with
![]() (39)
(39)
where ![]() is the energy dispersion of the lowest bound states.
is the energy dispersion of the lowest bound states.
In the high-temperature limit we have![]() , with a high-temperature entropy
, with a high-temperature entropy ![]() as it should be for a model with two states per site.
as it should be for a model with two states per site.
Critical XXZ chain: the dispersion relation of the free states is [36]
![]() (40)
(40)
At ![]() the model is critical and the correlation lengths diverges like
the model is critical and the correlation lengths diverges like![]() . In low-temperature we have that the expression for the entanglement reduces a simplest form given by
. In low-temperature we have that the expression for the entanglement reduces a simplest form given by
![]() (41)
(41)
where![]() , is the spin wave velocity.
, is the spin wave velocity.
6. Conclusion
In summary, we have calculated the entanglement in a quantum wire given by the quantum spin-1/2 anisotropic one-dimensional Heisenberg antiferromagnet. We verify the influence of quantum phase transition in the points of ![]() and
and![]() , which correspond to
, which correspond to ![]() and
and ![]() points, on entanglement. We use the Bethe’s ansatz method to calculate the entanglement
points, on entanglement. We use the Bethe’s ansatz method to calculate the entanglement ![]() since it is an exact method to the one-dimensional spin-1/2 Heisenberg chains. Our calculations show that the entanglement is maximum in the point
since it is an exact method to the one-dimensional spin-1/2 Heisenberg chains. Our calculations show that the entanglement is maximum in the point ![]() and the entanglement is minimum when
and the entanglement is minimum when![]() . Consequently there is a large influence of the quantum critical region on the entanglement. The influence of the quantum phase transition obtained for this system is large as obtained in Reference [1] for the extended Hubbard model for a finite number of particles N.
. Consequently there is a large influence of the quantum critical region on the entanglement. The influence of the quantum phase transition obtained for this system is large as obtained in Reference [1] for the extended Hubbard model for a finite number of particles N.
Acknowledgements
This work was partially supported by the Brazilian agencies FAPEMIG, CNPq and CEFET-MG.