Reflected BSDEs Driven by Lévy Processes and Countable Brownian Motions

Jean-Marc Owo

UFR de Mathématiques et Informatique, Université Félix H. Boigny, Abidjan, Côte d’Ivoire.

DOI: 10.4236/am.2015.614197                

Abstract

A new class of reflected backward stochastic differential equations (RBSDEs) driven by Teugels martingales associated with Lévy process and Countable Brownian Motions are investigated. Via approximation, the existence and uniqueness of solution to this kind of RBSDEs are obtained.

Keywords

Backward Doubly Stochastic Differential Equations, Lévy Processes, Teugels Martingales, Countable Brownian Motions

Received 25 March 2015; accepted 20 December 2015; published 23 December 2015

1. Introduction

Recently, Y. Ren [1] proved via the Snell envelope and the fixed point theorem, the existence and uniqueness of a solution for the following RBDSDEs driven by a Lévy process and a extra Brownian motion with Lipschitz coefficients, where the obstacle process is right continuous with left limits (càdlàg):

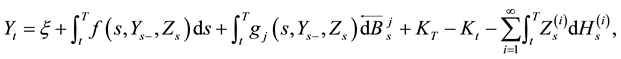
where the 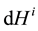is a forward semi-martingale Itô integrals (see He et al. [2] ) and the 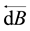is a backward Itô integral.

Note that, in all the previous works, the equations are driven by finite Brownian motions. In their recent work, Pengju Duan et al. [3] introduced firstly the reflected BDSDEs driven by countable extra Brownian motions:

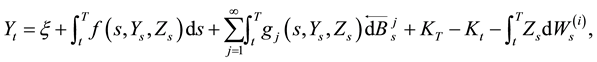(1.1)

where the dW is the standard forward stochastic Itô integral and the 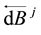is the backward stochastic Itô integral. Under the global Lipschitz continuity conditions on the coefficients f and g, they proved via Snell envelope and fixed point theorem, the existence and uniqueness of the solution for RBDSDEs (1.1). Next, J.-M. Owo [4] relaxed the Lipschitz continuity condition on the coefficient f to a continuity with sub linear growth condition and derive the existence of minimal and maximal solutions to RBSDEs (1.1).

Motivated by [1] [3] [4] , in this paper, we mainly consider the following RBDSDEs driven by a Lévy process and countable Brownian motions, in which the obstacle process is right continuous with left limits (càdlàg):

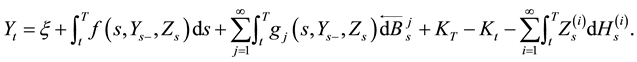(1.2)

The paper is devoted to prove the existence and uniqueness of a solution for RBSDEs driven by a Lévy process and countable Brownian motions.

The paper is organized as follows. In section 2, we give some preliminaries and notations. In section 3, we establish the main results.

2. Preliminaries and Notations

Throughout this paper, T is a positive constant and 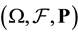is a probability space on which, 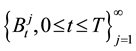are mutual independent one-dimensional standard Brownian motions and 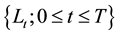be a 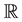-valued pure jump Lévy process of the form 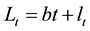independent of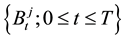, which correspond to a standard Lévy

measure 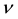satisfying 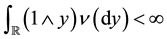and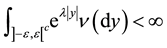, for every and for some.

Let denote the class of P-null sets of. For each, we define

where for any process;,.

Note that is an increasing filtration and is a decreasing filtration. Thus the

collection is neither increasing nor decreasing so it does not constitute a filtration.

Let us introduce some spaces:

・ denotes the space of real-valued processes such that is -measurable, for a.e. and.

・ denotes the sub set of formed by the -predictable processes;

・ stands for the set of real-valued, càdàg, random processes such that is - measurable, for any and.

・ denotes the space continuous, real-valued, increasing processes, such that is - measurable, for a.e., and.

・ denotes the set of real valued sequences such that

We will denote by and the corresponding spaces of -valued processes such that

In the sequel, for ease of notation, we set.

Furthermore, we denote by the Teugels Martingale associated with the Lévy process. More precisely

where for all and are power-jump processes. That is, and for, with.

In [5] , Nualart and Schoutens proved that the coefficients correspond to the orthonormalization of the polynomials with respect to the measure, i.e. . The martingale can be chosen to be pairwise strongly orthonormal martingale. That is, for all,.

Definition 2.1. A solution of a (1.2) is a triplet of -valued process, which satisfies (1.2), and

1)

2)

3) K is a continuous and increasing process with and

Throughout the paper, we let the coefficients and, the terminal value and the obstacle satisfying the following assumptions:

(H1) for all, are -measurable such that

(H2) for all and,

where, and are constants with and.

(H3), i.e. is a -measurable random variable such that, ,

(H4) S is a real-valued, càdàg process such that is -measurable, for a.e. and a.s.,

with, where. Moreover, we assume that its jumping times are inaccessible

stopping times (see He et al. [2] ).

3. The Main Results

We first establish the existence and uniqueness result for RBSDEs driven by finite Brownian motions and a Lévy process:

(3.1)

For any, we have the following existence and uniqueness result.

Lemma 3.2. Assume (H1) - (H4). Then, there exists a unique solution of Equation (3.1).

Proof. For, we obtain the existence and uniqueness result due to Y. Ren [1] . For any, we can prove the desired result following the same ideas and arguments as in Y. Ren [1] : it is a straightforward adaptation of the proofs of Theorem 2 and Theorem 3 in Y. Ren [1] . Firstly, we consider the special case that is the function f and do not depend on (Y, Z), i.e., , for all. It suffices to replace suitably and in the proof of Theorem 2

respectively by and. On the other hand, it suffices to replace

, , C and in the proof of Theorem 3 respectively by,

, and. Therefore, we omit the details.

Now, we are ready to establish the main result of this paper which is the following theorem.

Theorem 3.3. Under assumptions (H1)-(H4), there exists a unique solution of Equation (1.2).

Proof. (Existence.) By Lemma 3.1, for any, there exists a unique solution of (3.1), denoted by , i.e., and

(3.2)

The idea consists to study the convergence of the sequence, and to establish that its limit is a solution of (1.2). To this end, we first establish the following estimates:

(3.3)

where is a non-negative constant independent of n. Indeed, applying Itô’s formula to, we have

From assumption (H2) and Young’s inequality, for any we have

Using again Young inequality, we have for any,

Since

we have, for any,

Therefore,

Consequently,

We choose such that, Then, there exists a constant, such that

Applying Gronwall’s inequality, we get

Therefore, we have the existence of a constant such that

which by Burkhölder-Davis-Gundy’s inequality provides

Now, we show that is a Cauchy sequence in. To this end, without loss of generality, we let. Then, by difference, we obtain

(3.4)

Applying Itô’s formula to, we get

(3.5)

Taking expectation in both side of (3.5) and noting that, we have

(3.6)

Using again Young’s inequality, assumption (H2) and the estimates (3.3), we obtain,

where.

Therefore, by Gronwall’s inequality, we have

which, by Burkholder-Davis-Gundy inequality provides

Well, from assumptions (H1)-(H2), we have

Consequently, we get,

(3.7)

Moreover, from (3.4) together with Hölder’s and Burkholder-Davis-Gundy’s inequalities, we have

which, together with assumption (H2) and (3.7), provides

(3.8)

Consequently, is a Cauchy sequence in which is a Banach space. Therefore, there exists a process, such that

(3.9)

Now, let us show that the process satisfies our Equation (1.2). From Cauchy- Schwarz inequality, together with (H2), we have

Also, by Burkhölder-Davis-Gundy’s inequality, we get

and

Now, from (H1)-(H2) and the fact that, we have

which implies that

Moreover,

Therefore,

On the other hand, from the result of Saisho [6] (see p. 465), we have

Finally, passing to the limit in (3.2), we conclude that is a solution of (1.2).

(Uniqueness.) Let be two solutions of (1.2).

Applying Itô’s formula to, we get

(3.10)

Taking expectation in both side of (3.10) and noting that, we have

(3.11)

Using again Young’s inequality and assumption (H2), we obtain,

Choosing, we have, a.e., for all. So, we have, a.e., for all.

On the other hand, since,

we have, a.e., for all. Then, we complete the proof.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Ren, Y. (2010) Reflected Backward Doubly Stochastic Differential Equations Driven by a Lévy Process. C. R. Acad. Sci. Paris, Ser. I, 348, 439-444.
[2]	Yan, J., He, S. and Wang, J. (1995) Semimartingale and Stochastic Analysis. Scientific Press, Beijing,
[3]	Duan, P.J., Ren, M. and Fei, S.L. (2013) Reflected Backward Stochastic Differential Equations Driven by Countable Brownian Motions. Journal of Applied Mathematics, 2013, Article ID: 729636.
[4]	Owo, J.-M. (2015) Reflected Backward Stochastic Differential Equations Driven by Countable Brownian Motions with Continuous Coefficients. Electronic Communications in Probability, 20, 1-11. http://dx.doi.org/10.1214/ECP.v20-3771
[5]	Nualart, D. and Schoutens, W. (2001) Backward Stochastic Differential Equations and Feynman-Kac Formula for Lévy Processes with Applications in Finance. Bernoulli, 7, 761-776. http://dx.doi.org/10.2307/3318541
[6]	Saisho, Y. (1987) SDE for Multidimensional Domains with Reflecting Boundary. Probability Theory and Related Fields, 74, 455-477. http://dx.doi.org/10.1007/BF00699100