Multi-Energy Simulation of a Smart Grid with Optimal Local Demand and Supply Management ()
Received 13 November 2015; accepted 15 December 2015; published 18 December 2015


1. Introduction
With the emergence of renewable energy generation and storage technologies, like e.g. solar panels or batteries, the notion of smart grids has been developed [1] . Buildings can be equipped with these technologies to generate, store and (re-)distribute energy [2] . Moreover, a smart grid also suggests that (almost) all devices in a building are equipped with smart-meters to measure their consumption and are connected to a (local) network [3] [4] . In addition, the buildings of the smart grid are connected to a communication network to exchange information. Following this approach, a (software) agent may be employed in a building to autonomously and economically manage demand and supply of the building’s inhabitants. Such an agent also acts as energy consumption scheduler (ECS) [5] to optimally plan ahead and operate its associated devices accordingly. This can be extended from one building to the entire grid by allowing the agents to communicate with each other and coordinate their demand and supply. Consequently, peaks in the demand can be alleviated by temporarily shifting their loads to obtain a flatter load profile (load-shifting). This reduces the maximal grid load (peak-shaving) and also has beneficial monetary effects in demand-response scenarios, e.g. [6] .
The smart grid model in this paper adopts approaches from [5] [7] . It is represented by a discrete time dependent optimisation problem. The constraints describe the capabilities and limits of each agent. The objective function in [7] maximises global welfare, and in [5] minimises each agent’s costs. Both approaches consider only electrical power as energy and the demand-side of agents. In this paper, the above approaches are extended by additional types of energy, namely thermal energy (heat) and gas. Moreover, the energy production of each agent is also taken into account, i.e. the supply-side, to minimise each agent’s costs. The supply-side allows the agents not only to optimise the demand, but also to act as small-scale supplier, permitting decentralised energy generation. In addition, the smart grid structure is taken into account to realise distances between buildings, connectivity and line capacities, which was not done in [5] [7] , but e.g. in [8] .
In order to be able to represent an agent which is capable to utilise the three types of energy, manage the demand-side and also act as a supplier, a selected set of prototype devices are modelled in detail (Section 3). A solar panel can generate power “for free”. It generates power from insolation which requires taking weather data into account. Moreover, the insolation and environmental temperature from weather data influence not only the solar panels’ power generation but also the temperature in the building. A fuel cell is used as a prototype appliance for cogeneration. It is used to generate thermal energy and power by consuming gas. Its purpose is to allow gas as an alternative resource for heating. A battery is used to store power which is essential for peak- shaving, because the required power can be bought at off-peak times and stored until it is needed, as in e.g. [6] [9] [10] . Finally, a smart refrigerator as a sample smart appliance is taken into account. Its dependence on the temperature and the usage is a good example to represent optimal control with respect to fixed environmental influence. The agent is in addition associated with a fixed base power demand and a fixed base thermal energy emission by other appliances (such as e.g. TV or stove) which cannot be changed.
The agents participate in a cooperative bargaining game according to which they determine their respective optimal strategy to minimise costs (Section 4). This game is introduced to relate energy prices with demand. This allows the agent to compute price-aware optimal strategies. As a consequence, the prices rise at high demand and drop, even below zero, at higher supply than demand.
The bargaining game is designed such that a unique Nash equilibrium exists and is attained by iteratively computing each agent’s best-response independently. The computation of the best-response is determined by solving a quadratic optimisation problem with complementarity constraints (Section 3) which includes, aside a base power load profile, the employment of solar panels, fuel cells, batteries, central heating, and refrigerators. After the Nash equilibrium has been found, the demand and supply are distributed in the smart grid to meet each agent’s requirements. This is done by solving a multi-commodity flow problem through the smart grid (Section 2). If no feasible multi-commodity flow exists, the agents are restricted in their actions to enforce a feasible flow.
Concluding this paper, in Section 5 test cases are presented and discussed. The impact of the different devices and combination of devices are pointed out. In particular, the total and relative costs reduction with respect to other device combinations along with the relation to the peak-to-average ratio (PAR) is elaborated. Peak-shaving could be observed even for a relative small-capacity battery which makes the power load profile almost flat. The fuel cells are used as a surrogate for heating, reducing the costs, but increasing the PAR. The high power generation of solar panels forces the prices of power to drop below zero when the sun shines, if the demand is not high enough to consume the generated power.
2. Flow through the Smart Grid
Numerous approaches to model smart grids have been published, e.g. [6] [7] [11] . When modelling a smart grid, the main focus is in formulating the capabilities and limitations of each agent and how they can interact. The smart grid structure itself is neglected, assuming no limitations as e.g. in [6] [7] [11] . In this paper, however, the smart grid structure and capabilities are incorporated, similar to [8] , to be able to model an energy grid.
The presented approach is used to compute a feasible solution. This is done by computing the multi-com- modity flow set by the agents. If this is a feasible solution, nothing else needs to be done. If no feasible solution exists, the demand of all agents in total is reduced by the amount by which the capacities are exceeded. Incorporating this reduction into the agents’ optimisation process (Section 3) yields a feasible solution, excluding the cases where the agents cannot comply with the reduction. This is the case when the line capacities are inadequate, but this is not further treated in this paper.
Extending the approach from [8] , the smart grid is represented by a multi-commodity flow network. Since the smart grid in this paper deals with three types of energy and is time dependent, the standard notation for multi- commodity networks is extended by the types of energy and a temporal variable t. Therefore, consider a fixed discrete time interval 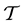 for which the simulation is carried out. Furthermore, let the set of all three types of energy (power, heat and gas) be denoted by
for which the simulation is carried out. Furthermore, let the set of all three types of energy (power, heat and gas) be denoted by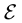 . A multi-commodity flow network for a type of energy
. A multi-commodity flow network for a type of energy 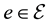 is a directed, connected graph
is a directed, connected graph 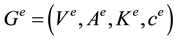 with a set of nodes
with a set of nodes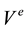 , a set of arcs
, a set of arcs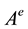 , a set of commodities
, a set of commodities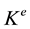 , and a capacity function
, and a capacity function 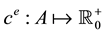 [12] . A commodity is defined as a triple
[12] . A commodity is defined as a triple 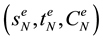 which specifies a demand
which specifies a demand 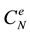 which is routed from source
which is routed from source 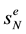 to sink
to sink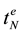 . The entire grid is given by
. The entire grid is given by
 . The nodes in
. The nodes in 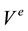 can be associated with different roles, such as power plants (source), another
can be associated with different roles, such as power plants (source), another
grid operator (sink), agents, and substations. Let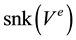 ,
, ![]() , and
, and ![]() denote the set of the network’s sinks, sources, and agents, respectively. Note that the flow of each type of energy is independent from each other. Each type of energy uses its own sinks and sources, substations and arcs. The only intersection of the networks are the agents, so that
denote the set of the network’s sinks, sources, and agents, respectively. Note that the flow of each type of energy is independent from each other. Each type of energy uses its own sinks and sources, substations and arcs. The only intersection of the networks are the agents, so that ![]() for any
for any![]() .
.
The multi-commodity flow of each type of energy can be computed separately. Therefore, in the following, the solution of an energy type e is exemplarily elaborated. The textbook approach to express the multi-com- modity flow as a linear optimisation problem is given by [12] as
![]() (1)
(1)
![]()
![]()
![]() denotes the flow of energy type e through the arc from N to M at time t and
denotes the flow of energy type e through the arc from N to M at time t and ![]() denotes a constant line loss. The constraints must hold for all
denotes a constant line loss. The constraints must hold for all![]() . The first constraint conserves the flow in the network.
. The first constraint conserves the flow in the network. ![]() can take arbitrary real values.
can take arbitrary real values. ![]() represents a demand,
represents a demand, ![]() a supply. The second constraint ensures that the line capacities are not exceeded. The objective function minimises the flow from sources and to sinks. A convenient effect of this is that only the minimal flow through the network is computed.
a supply. The second constraint ensures that the line capacities are not exceeded. The objective function minimises the flow from sources and to sinks. A convenient effect of this is that only the minimal flow through the network is computed.
If no feasible multi-commodity flow exists, we want to be able to determine why it does not exist. Two parameters can be changed to make the flow feasible: The agents’ demands and the grid capacities. Augmenting the grid capacities is a long-term and (financially) expensive process, whereas changing the demands is a short-term process. In this paper, the possibility of increasing the grid capacities is not discussed, because the presented approach aims at a fine temporal resolution (about 15 minutes). Limiting the demands may be unfavourable for the agents, in particular if the demands need to be changed in a way which is difficult to comply for the agent. The case that agents cannot comply is not discussed.
The amount of insufficient grid capacity needs to be identified and then communicated to all agents. This amount is determined by extending the linear optimisation problem (1) by a penalty term![]() :
:
![]() (2)
(2)
![]()
![]()
![]()
![]() is an arbitrary chosen penalty factor and the constraints must hold for all
is an arbitrary chosen penalty factor and the constraints must hold for all![]() . This optimisation problem minimises the violation of excess of the grid’s capacities and the minimum flow. In particular,
. This optimisation problem minimises the violation of excess of the grid’s capacities and the minimum flow. In particular,
![]() is the total excess at time t. If this sum is equal to zero, the agents’ demands do not exceed the
is the total excess at time t. If this sum is equal to zero, the agents’ demands do not exceed the
grid’s capacities and a solution is found. If the sum is greater than zero, the agents need to reduce their demands in total by that amount. A straight-forward approach is to uniformly distribute this excess over all agents.
The multi-commodity flow problem essentially depends on the demands ![]() which have to be met. In the following section, the computation of the values
which have to be met. In the following section, the computation of the values ![]() is elaborated by introducing agents in detail.
is elaborated by introducing agents in detail.
3. Agents in the Smart Grid
The actions and decisions an agent can autonomously perform are computed by a discrete time dependent quadratic optimisation problem. Its objective is minimising the costs. The details of the cost function are presented in Section 4. In this section, the incorporation of the agents’ demand and supply is elaborated, i.e. the constraints of the optimisation problem. The notation from the previous section is used to denote the considered discrete time interval by ![]() and the set of all types of energy by
and the set of all types of energy by![]() . Furthermore, all optimisation variables are non-negative and have an finite upper bound, unless otherwise noted.
. Furthermore, all optimisation variables are non-negative and have an finite upper bound, unless otherwise noted.
The balance constraint of an agent N at time step ![]() for type of energy
for type of energy ![]() is directly derived from the first constraint of the optimisation problem (2). So
is directly derived from the first constraint of the optimisation problem (2). So
![]() (3)
(3)
holds. This balance equation must be satisfied for all time steps t and for all types of energy![]() .
. ![]() is the produced energy and
is the produced energy and ![]() is the energy demand of device d from the set of devices
is the energy demand of device d from the set of devices ![]() of energy type e. The devices in
of energy type e. The devices in ![]() are presented below and contain solar panels, batteries, fuel cells, central heating, refrigerators, as well as a fixed base demand/supply of all other appliances. Every agent N requires a minimum amount of
are presented below and contain solar panels, batteries, fuel cells, central heating, refrigerators, as well as a fixed base demand/supply of all other appliances. Every agent N requires a minimum amount of
power ![]() and generates a minimum amount of thermal energy by operating devices
and generates a minimum amount of thermal energy by operating devices![]() . Both quantities
. Both quantities
are fixed but vary over time and are derived from a standard load profile [13] . Following [14] , the power base load is computed by using the standard load profile as mean value in a geometric distribution; the thermal energy base generation is used in a normal distribution.
An agent is restricted to either buy or sell energy of the same type within one time step. This is ensured by adding the complementarity constraint
![]() (4)
(4)
Since the inflow or outflow must be zero, only the net flow to and from an agent is considered in the optimisation problem. This is an important property when determining the optimum of the objective function in Section 4.
In the following sections, the devices an agent N operates are presented and how they contribute to the total energy produced ![]() and the total demanded energy
and the total demanded energy![]() . With the constraints presented in these sections a feasible set of solutions
. With the constraints presented in these sections a feasible set of solutions ![]() for the agent N is defined. It is assumed that
for the agent N is defined. It is assumed that ![]() is non-empty as to exclude infeasible scenarios. For the sake of simplicity of the notation, in the following the index denoting the building in the smart grid is omitted, so e.g.
is non-empty as to exclude infeasible scenarios. For the sake of simplicity of the notation, in the following the index denoting the building in the smart grid is omitted, so e.g. ![]() is written as
is written as![]() .
.
3.1. Solar Panel
The solar panel is a prototype of renewable energy generation. It generates power from environmental influences, in this case insolation, with respect to the temperature. A wind power plant would also fall in this category. The solar panel is of more interest in this paper, because only residential buildings are considered. These buildings can easily be equipped with solar panels, whereas a wind power plant in the backyard is rather undesired.
The solar panel is modelled according to [15] [16] . In [15] an implicit formulation of the generated electrical energy is given with respect to the outside temperature and insolation. With this approach the generated electrical energy is computed from real weather data, e.g. [17] . Since it is only dependent on the (fixed) properties of the solar panel, the temperature, and the insolation, the generated electrical energy can be pre-computed for all time steps, independent of the optimisation problem. So the electrical energy ![]() generated by a solar panel is merely a fixed term for each time step:
generated by a solar panel is merely a fixed term for each time step:
![]()
3.2. Fuel Cell
The fuel cell is a prototype device for cogeneration. It consumes gas and generates both, electrical power and thermal energy, in this paper. So it can be used as alternative to heat the building. The fuel cell is represented by two coupled generators, one for heat and one for power, similar to [14] . Both generators are described by the constraints
![]()
![]()
![]() is the amount of the consumed gas to produce energy and
is the amount of the consumed gas to produce energy and ![]() is the (constant) efficiency. The right-hand side of both constraints model start-up and shut-down phases.
is the (constant) efficiency. The right-hand side of both constraints model start-up and shut-down phases. ![]() is the duration of the start-up and shut- down phase in time steps, and
is the duration of the start-up and shut- down phase in time steps, and ![]() is the upper energy production bound of the respective generator.
is the upper energy production bound of the respective generator. ![]() indicates how the generator is operated.
indicates how the generator is operated.
3.3. Battery
Batteries play a substantial role in the smart grid. It is possible to store power from, e.g. solar panels, for a later point in time, in case it is currently not needed. Additionally, in demand-response scenarios, they flatten the peaks in the grid’s load profile [9] [10] and thus relieve the grid capacities. From a modelling point of view, however, a battery is abstracted from its physical realisation to its capabilities: A battery can either be charged by ![]() or discharged by
or discharged by ![]() in a time step, and has a maximum capacity
in a time step, and has a maximum capacity ![]() [6] . This is represented by the constraint
[6] . This is represented by the constraint
![]()
![]() specifies an efficiency of the storage,
specifies an efficiency of the storage, ![]() the charge efficiency, and
the charge efficiency, and ![]() the discharge efficiency.
the discharge efficiency. ![]() is the amount by which the battery is charged and
is the amount by which the battery is charged and ![]() by which it is discharged. To prohibit charging and discharging at the same time, effectively bypassing the storage loss, the complementarity constraint
by which it is discharged. To prohibit charging and discharging at the same time, effectively bypassing the storage loss, the complementarity constraint
![]() (5)
(5)
is employed.
3.4. Central Heating
A thermodynamic model similar to [7] is developed in this section with the goal to describe how much thermal energy is required to keep the temperature inside a building within a certain comfort interval, i.e. between the boundaries ![]() and
and![]() . In order to derive a suitable discrete time formulation for the optimisation problem, we start off with continuous time formulas which in turn are temporally discretised.
. In order to derive a suitable discrete time formulation for the optimisation problem, we start off with continuous time formulas which in turn are temporally discretised.
The total thermal energy flux inside a building ![]() is the sum of all contributing energy sources and sinks
is the sum of all contributing energy sources and sinks
![]() (6)
(6)
where ![]() denotes the combined fluxes of thermal convection and conduction,
denotes the combined fluxes of thermal convection and conduction, ![]() the flux caused by insolation,
the flux caused by insolation, ![]() is the heat flux of the devices (see (3)).
is the heat flux of the devices (see (3)). ![]() is the energy added or removed by heating, ventilating, and air conditioning and thus allows to actively change the temperature in a building. The terms of (6) other than
is the energy added or removed by heating, ventilating, and air conditioning and thus allows to actively change the temperature in a building. The terms of (6) other than![]() , which are elaborated below, rather represent passive changes due to the environment.
, which are elaborated below, rather represent passive changes due to the environment.
The thermal conduction and convection are expressed only with respect to the temperature difference of the inside and outside temperature ![]() and
and ![]() [7] [18]
[7] [18]
![]()
![]() comprises thermal conductivity, heat transfer coefficient and the building properties.
comprises thermal conductivity, heat transfer coefficient and the building properties. ![]() is assumed to be constant.
is assumed to be constant. ![]() is a fixed quantity which is determined by real weather data [17] .
is a fixed quantity which is determined by real weather data [17] .
The thermal energy flux by insolation through windows is determined by
![]()
with ![]() representing the sensitivity to insolation and
representing the sensitivity to insolation and ![]() the flux of insolation. This is treated separately from conduction effects, because, as with the solar panel, real weather data from [17] was used to compute
the flux of insolation. This is treated separately from conduction effects, because, as with the solar panel, real weather data from [17] was used to compute![]() .
.
The above continuous time equations are discretised with the implicit Euler method. Thus we obtain from (6)
![]() (7)
(7)
using a fixed time step size![]() . If
. If ![]() is positive, its energy is used to heat the building and thus contributes to the heat demand of the central heating
is positive, its energy is used to heat the building and thus contributes to the heat demand of the central heating ![]() with
with![]() . Whereas if
. Whereas if ![]() is negative, it cools down the temperature with an air conditioner. Consequently,
is negative, it cools down the temperature with an air conditioner. Consequently, ![]() and
and![]() . With the computed total thermal energy within the building its temperature
. With the computed total thermal energy within the building its temperature ![]() is computed from
is computed from
![]()
m is the mass, ![]() the specific heat capacity of the building. Since a building is composed of several types of components, the term
the specific heat capacity of the building. Since a building is composed of several types of components, the term ![]() is assembled by the weighted average of its components.
is assembled by the weighted average of its components.
With this thermodynamic model, it is possible to compute the required thermal energy to keep the temperature within the admissible bounds. In fact, the relation
![]() (8)
(8)
can readily be used as constraint in the optimisation problem to enforce a temperature within the comfort interval.
3.5. Smart Refrigerator
As example of smart appliances the smart refrigerator is introduced here. A smart appliance is a device which is entirely operated by an agent, e.g. refrigerator, freezer, dish washer. [6] [7] suggest different types of smart appliance models. The feature about being operated by an agent is that it can be flexibly operated to shift load away from peak loads and/or reduce operation costs.
The refrigerator model is directly derived from the thermodynamic model (7) and (8) by changing the parameters and constants accordingly. This way also a freezer model can be derived.
There are two peculiarities to mention. One is that the temperature within the refrigerator is dependent on the temperature within the building, which in turn is dependent on the environmental temperature. So the temperature in the refrigerator can also be influenced by the central heating.
The other peculiarity is that items may be put in or removed from the refrigerator and thus the mass m of the refrigerator’s content is time dependent. When items are added, convective thermal energy is added and the mass of the refrigerator’s content increase. Analogous when items are removed, energy is removed and the mass is decreased.
Since the required thermal energy to stay within the admissible bounds is known from (7) and![]() , the electrical energy demand and thermal energy emission from the operating refrigerator are written as
, the electrical energy demand and thermal energy emission from the operating refrigerator are written as
![]()
![]()
![]() specifies how much thermal energy is emitted to the surroundings per unit of cooling when operating the refrigerator and
specifies how much thermal energy is emitted to the surroundings per unit of cooling when operating the refrigerator and ![]() specifies how much electrical energy is required to operate the refrigerator per unit of cooling.
specifies how much electrical energy is required to operate the refrigerator per unit of cooling.
4. Cooperative Bargaining Game
The prices of the types of energy play an essential role in the solution of the optimisation problem presented in Section 3 for each agent in the smart grid. The agents are assumed to act rationally and economically, so that they preferably consume energy when the prices are low and save or possibly sell energy when the prices are high. In contrast, the prices should reflect the efforts of the grid operator to supply its agents, and thus the production costs increase with increasing demand. Such a pricing model has to be designed which takes the above aspects into account.
At first, the total costs in the entire grid are determined with respect to the total demand and supply in the smart grid. Note that supply in this context refers to the agent generated supply and not to the grid operator’s supply. Subsequently, the total costs are fairly broken down to each agent. This results in the costs objective function which the respective agents seek to minimise.
There have been cooperative game theoretical approaches [5] [7] [19] which allow agents to schedule their demands in coordination with each other to achieve a fair, global optimum. The method in [19] is based on [5] and improves the fairness of the pricing scheme. In [7] a utility function is used rather than prices for optimisation.
The three mentioned references only deal with the demand-side. The approach presented in this paper expands [5] by allowing the agents to sell energy (supply-side), too. Fairness is achieved by applying the presented approach of [19] . However, no utility function is used in the presented approach; the entire behaviour of the players is determined by the prices. Furthermore, not only one type of energy is considered but three, in accordance with the smart building model in Section 3.
4.1. Total Costs in the Smart Grid
The central role in the price model has the grid operator. It acts budget balanced, i.e. neither generates profit nor suffers losses. Consequently, the energy is sold for the production price. The costs of a type of energy ![]() for the grid operator
for the grid operator ![]() is written as function of total demand of the agents
is written as function of total demand of the agents ![]() and total supply of the agents
and total supply of the agents ![]() in the smart grid. The newly introduced variables are defined as
in the smart grid. The newly introduced variables are defined as
![]() (9)
(9)
Below some properties of the cost function are stated from which a function ![]() is defined. Consider the balance between demand and supply
is defined. Consider the balance between demand and supply ![]() at a time step t. If this difference is zero, the grid is self- sustaining. In this case the grid operator does not supply the agents implying zero cost. If
at a time step t. If this difference is zero, the grid is self- sustaining. In this case the grid operator does not supply the agents implying zero cost. If![]() , the grid operator uses its power plants to produce energy or buys energy from another grid operator to meet the demand of the agents. These costs must be covered. If
, the grid operator uses its power plants to produce energy or buys energy from another grid operator to meet the demand of the agents. These costs must be covered. If![]() , the agents generate more energy than can be reasonably used in the smart grid. Since this surplus of energy cannot be stored in the smart grid, it is mandatory to transfer the energy to another grid (competitor); selling the energy at any price. Consequently, selling to a competitor yields a potential financial loss which is passed to the agents by increasing prices accordingly, and therefore discouraging overproduction.
, the agents generate more energy than can be reasonably used in the smart grid. Since this surplus of energy cannot be stored in the smart grid, it is mandatory to transfer the energy to another grid (competitor); selling the energy at any price. Consequently, selling to a competitor yields a potential financial loss which is passed to the agents by increasing prices accordingly, and therefore discouraging overproduction.
Summarising the three cases, an interpretation which penalises any deviation of a self-sustaining equilibrium ![]() is possible.
is possible. ![]() is therefore defined as the quadratic deviation from the equilibrium
is therefore defined as the quadratic deviation from the equilibrium
![]() (10)
(10)
![]() is a constant which allows differentiated weighting of the deviation for each type of energy. It is easy to check that
is a constant which allows differentiated weighting of the deviation for each type of energy. It is easy to check that ![]() is continuously differentiable, convex, and its minima are on the line
is continuously differentiable, convex, and its minima are on the line![]() . The entire costs in the smart grid for all types of energy
. The entire costs in the smart grid for all types of energy ![]() over all time steps
over all time steps ![]() is given by
is given by
![]() (11)
(11)
Summing up (10) the differentiability and convexity is preserved.
The cost function ![]() encourages the agents to use their devices to generate as much energy as demanded. This is an essential aspect of this function: If agents are encouraged to produce energy, they can supply their neighbours, because this yields a financial benefit for them. Additionally, in the entire grid the load is reduced, because energy generation is decentralised this way and the energy can be consumed where it is generated and does not need to be transferred through the entire grid.
encourages the agents to use their devices to generate as much energy as demanded. This is an essential aspect of this function: If agents are encouraged to produce energy, they can supply their neighbours, because this yields a financial benefit for them. Additionally, in the entire grid the load is reduced, because energy generation is decentralised this way and the energy can be consumed where it is generated and does not need to be transferred through the entire grid.
4.2. Individual Costs of Each Player
With the global costs in the smart grid defined in (11), fair prices for each agent are derived such that the global costs are covered. Based on [19] the fair pricing is proportional to each agent’s contribution to the global costs. So (10) can be reformulated with respect to the proportional contribution of agent N
![]() (12)
(12)
By applying (9), (10) and (12) can be shown to be equivalent. Through division by ![]() singularities are introduced, but these are removable. So the total costs (12) may be simplified:
singularities are introduced, but these are removable. So the total costs (12) may be simplified:
![]() (13)
(13)
From (13) the costs for an agent N with respect to its demand/supply and energy prices are given by
![]() (14)
(14)
This can be rewritten with respect to agent N and all other agents. For an agent N, only the variables indexed with N can be changed, the other terms are considered fixed. Therefore the game theoretic notation of the negative index ![]() is applied to denote a variable depending on all agents except agent N. So the costs for an agent N for energy type e in game theoretic notation is given by
is applied to denote a variable depending on all agents except agent N. So the costs for an agent N for energy type e in game theoretic notation is given by
![]()
The total cost of an agent N can be expressed analogously to the total cost in the grid in (11) by
![]() (15)
(15)
4.3. Bargaining Algorithm
With (15) it is possible to define a cooperative bargaining game. Since the configuration varies from agent to agent, the feasible set of the optimisation problem of agent N, as presented in Section 3, is denoted by![]() . Let the bargaining game be defined by:
. Let the bargaining game be defined by:
• Players: All agents![]() .
.
• Strategies: Each player N selects ![]() to maximise its pay-off.
to maximise its pay-off.
• Pay-offs: ![]() for agent N.
for agent N.
In game theory, a pay-off is maximised which in this case is equivalent to minimising costs. The pay-off interpretation is merely a game theoretic convention.
The above game falls in the category of N-person game with a concave pay-off function. By applying (4), the pay-off function becomes strictly concave. The existence and uniqueness of Nash equilibria in strictly concave N-person games was shown in [20] . A nash equilibrium characterises the optimal strategy of a game. It states that any unilateral deviation by a player from this equilibrium leads to a worse pay-off [21] . Consequently, if ![]() are the strategies of the Nash equilibrium,
are the strategies of the Nash equilibrium,
![]() (16)
(16)
holds for all ![]() and for all
and for all![]() . If each agent iteratively plays its best-response strategy to maximise their pay-off, eventually the Nash equilibrium is attained [5] [20] . This procedure is illustrated in Algorithm 1 [9] . With this algorithm, the earlier defined bargaining game computes a global optimum which in turn is optimal for each agent.
. If each agent iteratively plays its best-response strategy to maximise their pay-off, eventually the Nash equilibrium is attained [5] [20] . This procedure is illustrated in Algorithm 1 [9] . With this algorithm, the earlier defined bargaining game computes a global optimum which in turn is optimal for each agent.
The optimisation problem which needs to be solved for each agent is a quadratic optimisation problem with complementarity constraints. The objective function and the constraints (4) and (5) are complementary. The other constraints, as presented in Section 3, are linear. By means of the penalty method it is possible to move the complementarity constraints to the objective function and leave the linear constraints unchanged [22] [23] . As a result a new pay-off function for an agent N is given by
![]() (17)
(17)
with a penalty factor r. This optimisation problem has the same optimum as the original optimisation problem for ![]() [23] . In [22] [24] [25] it was shown that the above approach converges despite of the complementarity constraints which violate the linear independence constraint qualification.
[23] . In [22] [24] [25] it was shown that the above approach converges despite of the complementarity constraints which violate the linear independence constraint qualification.
With the reformulation in (17), only linear constraints are left. So merely a quadratic linear optimisation problem needs to be solved. There are various ways to solve such kind of problems, e.g. interior point method, augmented Lagrangian methods, or conditional gradient method [23] [26] [27] . In this paper, the conditional gradient method [28] is used, because it can be easily obtained by extending the simplex algorithm, see e.g. [29] , which is already used to compute the multi-commodity flow in Section 2. In the following section, test cases are presented to illustrate the fairness and the economical usefulness of this approach.
5. Simulations
The tests in this section are carried out in scenarios in which the energy demand and weather data are known for all time steps. The simulation of one day during winter with time step size of 15 minutes of nine buildings used the following specifications for each building: The building’s admissible room temperature is from 2025. The fuel cell losslessly generates thermal and electrical energy in a 2:1 ratio and needs 30 minutes to start-up and shut-down, respectively. The maximal thermal power generation is 2.6. The battery can store up to 1 of electrical energy losslessly and at most 0.4 can be fed in or out of it. The solar panel has a peak output power of 2.4. The refrigerator has a temperature tolerance interval of 37 and cooling power of 0.09. Note that the devices in the buildings are identical, but the base demand of electrical power and base thermal energy generation varies from building to building, because they are probabilistically generated as described in Section 3.
The grid operator distributes electrical power, thermal energy and gas over the smart grid. The agents can only sell electrical power and thermal energy; gas can only be consumed.
![]()
Algorithm 1.Bargaining game algorithm over a time interval![]() .
.
In the tested scenarios, the buildings were equipped with every possible combination of the above mentioned devices. Only the refrigerator was included in every test case. GNU linear programming kit (glpk) [29] was used to solve the optimisation problem by applying its provided simplex routines in the conditional gradient method.
In the simulation the peak-to-average ratio (PAR) and the average costs per energy type are evaluated. The PAR relates the peak load in a time interval to the average load. If the peak load is identical to the average load, the PAR is equal to one and represents a perfectly flat load, which is desired. The PAR is depicted in Figure 1, the average unit costs and the total costs are shown in Figure 2.
Figure 1 shows that the PAR for heat is about 1.4 which is quite flat. This is owed to the fact that the central heating is part of the optimisation problem and minimising the costs for heating also entails a flat load. A similar relation between PAR and costs minimisation was already shown in [5] . In contrast, the power demand is mostly prescribed and therefore possesses fluctuations which cannot entirely be compensated but alleviated at best. The PAR for power is about 3.7 and can only be reduced by employing a battery. It reduces the PAR by 19% to approximately 3.0. The PAR for gas consumption is only plotted for the three cases which employ fuel cells, in the other cases the gas cannot be processed and is thus unused. It is, however, remarkable that in the scenarios with a fuel cell and fuel cell & solar panel the PAR for heat and power does not decrease. In fact, in most cases it increases. Since the objective function minimises the costs, the reduction of the PAR is a beneficial side-effect but not imperative.
![]()
Figure 1. PAR of each energy type for all test cases.
![]()
Figure 2. Total costs of the smart grid for each type of energy.
In Figure 2, the virtual costs for the above mentioned scenarios are plotted. The virtual costs are derived from (13) by setting ![]() and summing over all time steps
and summing over all time steps![]() , so that for a type of energy
, so that for a type of energy ![]() the virtual costs are
the virtual costs are
![]()
where demand and supply are measured in kilojoule. The virtual price is ![]() evaluated at each time step with
evaluated at each time step with![]() . In Figure 2, using the same colours and layout, the fuel cell significantly reduces the costs of heat and power. The reduction of costs is achieved by using gas in the fuel cell for heating instead the grid operator’s provided heat, because it is cheaper. The fuel cell cogenerates heat and power, so in addition to heat cheaper with gas, power generation is also included in this process “for free”. The other cases without fuel cell only have an impact on the prices of power, because they only relate to power. The solar panel hardly has an impact on the power prices, whereas the battery reduces them significantly. The total power costs drop by at least 36% when employing a battery.
. In Figure 2, using the same colours and layout, the fuel cell significantly reduces the costs of heat and power. The reduction of costs is achieved by using gas in the fuel cell for heating instead the grid operator’s provided heat, because it is cheaper. The fuel cell cogenerates heat and power, so in addition to heat cheaper with gas, power generation is also included in this process “for free”. The other cases without fuel cell only have an impact on the prices of power, because they only relate to power. The solar panel hardly has an impact on the power prices, whereas the battery reduces them significantly. The total power costs drop by at least 36% when employing a battery.
In another set of tests, the following devices’ properties were significantly increased: Solar panel’s peak output power was increased to 9.6, battery’s maximum capacity was increased 10 along with increased in-/outflow rates of 4, respectively, and fuel cell’s maximum thermal power generation was increased to 24; the other parameters and other devices and settings were left unchanged. The following test setting uses only one of the above augmented devices. This was carried out to ensure that certain effects can be attributed to a specific device and their properties. The relative change of quantities below refer to the same scenario with the non-augmented properties of the devices.
With the solar panels’ power generation increased a further drop in cost of 8% maximum could be observed along with an increase of the PAR between 1.5% to 4%. This causes the power prices to drop below zero when the sun shines, meaning that one is paid to consume power, as shown in Figure 3.
With the batteries’ increased properties, both, the PAR and costs, reduce further. The power costs decrease by 8% to 9.5%; the PAR is reduced up to 10%. With this behaviour the peak load in the grid can be alleviated by storing power when it is cheap (or is abundantly available) and use it or sell it when it is expensive, as depicted in Figure 4. The first two plateaus are due to the initial transient. From about hour 4 the plot is perfectly flat and even the highest peak in the simulation, just before hour 24, does not increase the overall load. Even with the 1 battery, the fluctuation could be significantly flattened.
Increasing the fuel cell’s power does not have any impact in the above scenarios. The reason for that is that the fuel cell is primarily used for heating and there is only a certain amount of demand to be meet. Thus being able to produce more has no further benefit.
6. Conclusions
In this paper a game theoretic approach for a multi-energy smart grid simulation has been proposed. The
![]()
Figure 3. Power prices in contrast to heat prices.
![]()
Figure 4. Total power demand with and without battery.
feasibility of the flow through the smart grid is computed by solving a modified multi-commodity flow problem. The demand and supply itself are computed by finding unique Nash equilibrium in a concave N-person game by iteratively computing the players’ best-response strategies to obtain minimal costs. These strategies are the solutions to the respective player’s quadratic optimisation problem with complementarity constraints. The objective function relates demand and supply to the costs by applying a fair pricing scheme.
The test results show that with this model solar panel, batteries and fuel cells can be used to reduce the energy prices to varying extent. The peak-to-average ratio (PAR) can only be reduced significantly by employing batteries. Solar panels increase the PAR when the sun shines. Moreover, when solar panels generate more power than can be consumed, the prices for power drop below zero. Fuel cells replace the heating and therefore do not flatten the demand but use gas as a heating surrogate. This entails that the heat demand is reduced but the gas demand is increased, which overall yields a financial profit.
A further step is to increase the simulation to city-sized grid to compute the individual behaviour and compare local sub-grid (distributed) optimisation with centralised (global) optimisation. Since the implementation was carried out in C++ and the open source GNU linear programming kit [29] for solving the optimisation problems, much larger scenarios than the ones presented here are possible to simulate. In particular, running distributed parallel computations allows simulating realistic-sized smart grids.
NOTES
![]()
*Corresponding author.