A New One-Twelfth Step Continuous Block Method for the Solution of Modeled Problems of Ordinary Differential Equations

Emmanuel Adegbemiro Areo, Micheal Temitope Omojola

Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria.

DOI: 10.4236/ajcm.2015.54039                

Abstract

In this paper, we developed a new continuous block method by the method of interpolation and collocation to derive new scheme. We adopted the use of power series as a basis function for approximate solution. We evaluated at off grid points to get a continuous hybrid multistep method. The continuous hybrid multistep method is solved for the independent solution to yield a continuous block method which is evaluated at selected points to yield a discrete block method. The basic properties of the block method were investigated and found to be consistent, zero stable and convergent. The results were found to compete favorably with the existing methods in terms of accuracy and error bound. In particular, the scheme was found to have a large region of absolute stability. The new method was tested on real life problem namely: Dynamic model.

Keywords

Power Series Approximate Solutions, Consistent, Zero Stability, Continuous Block Method, Dynamic Model

Received 22 October 2015; accepted 13 December 2015; published 16 December 2015

1. Introduction

In this paper, we considered the method of approximate solution of the general second order initial value problem of the form

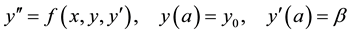(1)

where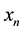, is the initial point, 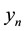is the solution at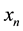, f is continuous within the interval of integration.

Equation (1) is of interest to researchers because of its wide application in engineering, control theory and other real life problem, hence the study of the methods of its solution. Hence, authors proposed methods with different basis functions and among them are [1] -[9] to mention a few.

Block method was later proposed. This block method has the properties of Runge-kutta method for being self-starting and does not require development of separate predictors or starting values. Among these authors are [10] -[12] . Block method was found to be cost effective and gave better approximation.

In this paper, we propose a new one-twelfth step continuous hybrid block method for the numerical inte- gration of second order initial value problems with constant step-size which is then implemented in block mode.

The paper is organized as followed: Section 2 considers the mathematical formulation of the method. Section 3 considers the analysis of the basic properties of the method. Section 4 considers the Region of absolute stability of our method. Section 5 considers the application of the derived method to solve some second order Ordinary Differential Equations and conclusion.

2. Mathematical Formulation of the Method

We consider the simple power series as a basis function for approximation:

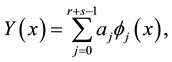(2)

where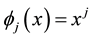

And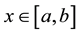,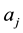’s are coefficients to be determined and is a polynomial of degree. We construct a k-step collocation method (MCM) by imposing the following conditions on (2)

(3)

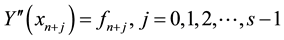(4)

Substituting (1) into (4) gives

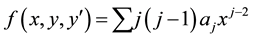(5)

We shall consider a step-length of 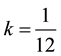with a constant step-size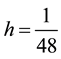

Interpolating (3) at 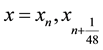and collocating (4) at gives a system of non- linear equation of the form

(6)

where and

Solving (6) for the’s and substituting back into (3) and after much algebraic simplification, we obtained

(7)

where

(8)

Evaluating (2) at gives the main method below,

(9)

(10)

(11)

The Predictors are expressed as follows:

(12)

(13)

(14)

(15)

(16)

Formation of the Block for One-Twelfth Step Block Method

The combination of Equations (9), (10), (11) and (12), yield the block of the form

(17)

Writing (17) explicitly gives

(18)

(19)

(20)

(21)

Substituting (18) into (13)-(16) gives the following Block-Predictor as follows

(22)

(23)

(24)

(25)

3. Basic Properties of One-Twelfth Step Method

3.1. Order and Error Constant of the Block

Let the linear operator defined on the method be, Where,

(26)

Expanding the form and in Taylor series and comparing coefficients of h, we obtained

Definition: The linear operator and the associated block method are said to be of order p if

. is called the error constant. It implies that the local truncation

error is given by

Expanding the block in Taylor series expansion gives

(27)

Comparing the coefficients of h, the order of the block is p = 5

With error constant

3.2. Consistency

In numerical analysis, it is necessary that the method satisfies the necessary and sufficient conditions.

A numerical method is said to be consistent if the following conditions are satisfies

1) The order of the scheme must be greater than or equal to 1 i.e..

2)

3)

4)

where, and are the first and second characteristics polynomials of our method. According to [3] , the first condition is a sufficient condition for the associated block method to be consistent. Our method is order. Hence it is consistent.

3.3. Zero Stability of the Method

The general form of block method is given as

(28)

Applying (22)-(25) to (26) gives

Since no root has modulus greater than one and is simple, the block method is zero stable in the

4. Region of Absolute Stability of the Block Method

According to Areo and Adeniyi [12] , we express this stability matrix

(29)

together with the stability function

(30)

Hence, we express the block method (18) in form of

(31)

(32)

The elements of the matrices A, B, U and V are substituted and computing the stability function with Maple software yield, the stability polynomial of the method which is then plotted in MATLAB environment to produce the required absolute stability region of the methods, as shown by the figure below

The graph Figure 1 shows that our method is A-Stable and the plot covers a large region of the complex plane

5. Implementation of the Method

In this section, we discuss the strategy for the implementation of the method. In addition, the performance of the method is tested on some modeled examples of second order initial value problems in Ordinary Differential Equations. Absolute error of the approximate solution are then compared with the existing methods. In particular, the comparison are made with those proposed by Awoyemi et al. and Ehigie et al.

Discussion of the results of the methods are also done here.

5.1. Numerical Experiments

The method is tested on some numerical problems to test the accuracy of the proposed methods and our results are compared with the results obtained using existing methods.

The following problems are taken as test problems:

5.2. Implementation of the Method

5.2.1. Dynamic Problem

A 10-kg mass is attached to a spring having a spring constant of 140 N/m. The mass is started in motion from the equilibrium position with an initial velocity of 1 m/sec in the upward direction and with an applied external force. Find the subsequent motion of the mass if the force due to air resistance is

It follows from Newton’s second law

(33)

or

(34)

If the system starts at t = 0 with an initial velocity and from an initial position, we also have the initial conditions.

Figure 1. Region of absolute stability of our method.

(35)

Now if and. The equation of motion, (28) becomes

(36)

Applying the initial conditions and to (30), we use the maple function

(37)

We get the exact solution

(38)

Note that the exponential terms, which come from the homogeneous solution represent an associated free overdamped motion, quickly die out. These terms are the transient part of the solution. The terms coming from the particular solution however, do not die out at; they are the steady-state part of the solution.

5.2.2. Problem 2

(39)

Exact solution:

5.2.3. Problem 3

(40)

Exact solution:

5.2.4. Problem 4

(41)

Exact solution:

5.2.5. Problem 5

(42)

Exact solution:

5.2.6. Problem 6

(43)

Exact solution:

6. Conclusion

We have proposed a new one-twelfth step hybrid block method for the numerical solution of second order initial value problems of ordinary differential equations in this paper. The method is consistent, convergent and zero stable. The method derived efficiently solved second order Initial Value Problems as can be seen in the low error constant and hence better approximation than the existing methods as can be seen in Tables 1-6. We have

Table 1. Result of test problem 1.

Table 2. Result of test problem 2.

Table 3. Result of test problem 3.

Table 4. Result of test problem 4.

Table 5. Result of test problem 5.

Table 6. Result of test problem 6.

also applied our method to the dynamic problem and the result is as displayed in Table 1.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Osa, A.L. and Olaoluwa, O.E. (2015) Hybrid and Non-Hybrid Implicit Schemes for Solving Third Order ODEs Using Block Method as Predictors. Mathematical Theory and Modelling, 5, 10-26.
[2]	James, A.A., Adesanya, A.O., Sunday, J. and Yakubu, D.G. (2013) Half-Step Continuous Block Method for the Solutions of Modeled Problems of Ordinary Differential Equations. American Journal of Computational Mathematics, 3, 261-269. http://dx.doi.org/10.4236/ajcm.2013.34036
[3]	Adesanya, A.O., Odekunle, M.R. and James, A.A. (2012) Order Seven Continuous Hybrid Methods for the Solution of First Order Ordinary Differential Equations. Canadian Journal on Science and Engineering Mathematics, 3, 154-158.
[4]	Badmus, A.M. and Mishehia, D.W. (2011) Some Uniform Order Block Methods for the Solution of First Ordinary Differential Equation. JNAMP, 19, 149-154.
[5]	Fatokun, J., Onumanyi, P. and Sirisena, U.W. (2011) Solution of First Order System of Ordering Differential Equation by Finite Difference Methods with Arbitrary. JNAMP, 30-40.
[6]	Awoyemi, D.O., Adebile, E.A., Adesanya, A.O. and Anake, T.A. (2011) Modified Block Method for the Direct Solution of Second Ordinary Differential Equations. International Journal of Pure and Applied Mathematics, 181-188.
[7]	Onumanyi, P., Sirisena, U.W. and Jator, S.A. (1999) Solving Difference Equation. International Journal of Computing Mathematics, 72, 15-27. http://dx.doi.org/10.1080/00207169908804831
[8]	Areo, E.A., Ademiluyi, R.A. and Babatola, P.O. (2011) Three-Step Hybrid Linear Multistep Method for the Solution of First Order Initial Value Problems in Ordinary Differential Equations. JNAMP, 19, 261-266.
[9]	Areo, E.A. and Adeniyi, R.B. (2013) A Self-Starting Linear Multistep Method for Direct Solution of Second Order Differential Equations. International Journal of Pure and Applied Mathematics, Bulgaria, 82, 345-364.
[10]	Ibijola, E.A., Skwame, Y. and Kumleng, G. (2011) Formation of Hybrid of Higher Step-Size, through the Continuous Multistep Collocation. American Journal of Scientific and Industrial Research, 2, 161-173. http://dx.doi.org/10.5251/ajsir.2011.2.2.161.173
[11]	Bronson, R. and Costa, G. (2006) Differntial Equations. 3rd Edition, McGraw Hill, 115-121.
[12]	Ehigie, J.O., Okunuga, S.A., Sofoluwe, A.B. and Akanbi, M.A. (2013) On Generalized 2-Step Continuous Linear Multistep Method of Hybrid Type for the Integration of Second Order Ordinary Differential Equations. Archives of Applied Science Research, 2, 362-372.