Analysis of Sleep Window of IEEE802.16m Network Based on State Transition Chain ()
Received 29 October 2015; accepted 13 December 2015; published 16 December 2015


1. Introduction
In IEEE802.16, wireless metropolitan area networks (WMANs), mobile stations (MSs) consume less energy with sleep mode. This happened when they are served with realtime traffic and offline buffered traffic [1] . The existing 802.16 sleep mode has some shortcomings. Once the size of the listening window in IEEE802.16 is determined, it cannot be adjustable after that. For this mechanism, a base station (BS) cannot transmit traffic when MS’s listening window expires, though the BS has more traffic destined in the sleep mode. For this reason, the MS will face some traffic delay. In addition to this, in 802.16 standards, an MS allows multiple connections to manage multiple energy saving cycles (ESCs) independently for its connections, while multiple connections can also be mapped onto a single ESC. In the previous case, a sleep window in one ESC might overlap with the listening windows of other ESCs. Another point is that the MS doesn’t down its power on transceiver in such overlapped periods; as a result the energy cannot be saved. To overcome these drawbacks, the emerging 802.16m adopts the following new features: 1) One MS, one PSC (power saving class) in the sleep mode; and 2) the adjustable listening window which is dependent on BS’s buffer status and/or hybrid automatic repeat request (HARQ) retransmission state [2] . In this paper, we examine the impacts of these new strategies. Though many studies have been already made for the 802.16 sleep mode [4] -[9] , here we focus only on the new strategies of the 802.16m sleep mode by avoiding the common parts of the 802.16m and the 802.16 sleep modes.
The paper is organized as follows: in Section 2, we briefly explain the 802.16 m sleep mode operation. In Section 3, we present the system model of IEEE802.16m, and then obtain performance evaluation results in Section 4. Finally, the paper concludes in Section 5.
2. IEEE802.16m Sleep Mode
Now we present the summarized key advancements in the 802.16 m sleep mode. In the 802.16 sleep mode, it is likely that the MS maintains a separate power saving class for each of its associations. Hence, multiple listening windows and sleep windows might overlap each other, which degrades the power saving efficiency of the system and loses the objective of having several power saving classes. That is why for each MS, the 802.16 m simplifies the sleep mode operation by offering a single PSC. It means that the MS maintains a single PSC for all of its connections. It is to be mentioned here that different MS in the 802.16 m network might have different power saving classes. Traffic in different connections are mixed together and served within the same power saving class [10] .
The listening window size in the 802.16 sleep mode is fixed, but in the new 802.16 m sleep mode is that the listening window may be extended if there are packets buffered at the BS for the MS. For example during the second cycle (T2) depicted in Figure 1, the packets arriving during the initial listening window trigger the window extension, but the packets arriving during the first extension of the listening window extend the window further. The third achievement is related to sleep mode reconfiguration. MS’s sleep cycle length doubles every cycle till reaching and remaining at a maximum value when there is no traffic destined for it though the listening window length remains the same. For example, in Figure 1, the sleep cycle length doubles after the first cycle ( ) as there is no traffic during the first cycle, that is
) as there is no traffic during the first cycle, that is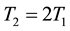 . However, when there is traffic destined for the MS, the IEEE802.16m sleep mode allows the sleep cycle to be either retuning to a minimum value or reset to an arbitrary value. The third cycle (T3) shown in Figure 1 is an example of such reconfiguration. The BS conveys this reconfiguration information to the MS via special signaling messages (e.g., AAI-SLPREQ) during the beginning of a sleep cycle. But in 802.16 sleep mode, the BS can only reconfigure the operational parameters of an MS after it deactivates the power saving class via more complicated signaling exchange [11] . In this paper, we study the following typical operation of the 802.16 m sleep mode:
. However, when there is traffic destined for the MS, the IEEE802.16m sleep mode allows the sleep cycle to be either retuning to a minimum value or reset to an arbitrary value. The third cycle (T3) shown in Figure 1 is an example of such reconfiguration. The BS conveys this reconfiguration information to the MS via special signaling messages (e.g., AAI-SLPREQ) during the beginning of a sleep cycle. But in 802.16 sleep mode, the BS can only reconfigure the operational parameters of an MS after it deactivates the power saving class via more complicated signaling exchange [11] . In this paper, we study the following typical operation of the 802.16 m sleep mode:
・ The BS will inform an MS about the buffered packet destined for it, an AAI-TRF-IND signaling message is sent at the beginning of each listening window.
・ The listening window is extended until the transmission queue at the BS is nonempty.
・ The entire listening window will be fully utilized for packet transmissions.
・ Sleep mode reconfiguration is done without disturbing the ongoing power saving class via special signaling messages.
・ The maximum length of the sleep cycle is a configurable parameter.
![]()
Figure 1. An example of IEEE802.16m sleep mode.
3. System Model
In IEEE802.16m, the active mode of an MS is known as “listening mode” while the inactive mode is known as “sleeping mode”. An MS performs two functions while is in listening window that are: 1) it is receiving all the packets buffered at the BS, and 2) after receiving all the buffered packets from the BS, the MS is not going to the sleeping mode instantly as there is a chance of receiving more packets from the BS. The MS has set a timer in on state for duration of , if the MS does not receive any packet buffered at BS within this
, if the MS does not receive any packet buffered at BS within this  time, then the MS goes to sleep mode. If the MS receives the packet within [0,
time, then the MS goes to sleep mode. If the MS receives the packet within [0, ] then it sets the timer again and wait for the duration [0,
] then it sets the timer again and wait for the duration [0, ] to see whether any new packet arrives or not. The algorithm will continue till arrival of no packets over [0,
] to see whether any new packet arrives or not. The algorithm will continue till arrival of no packets over [0, ], hence the MS reaches at the sleeping state.
], hence the MS reaches at the sleeping state.
If the probability density function (pdf) of interarrival time of packets follows the exponential pdf [12] , then
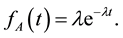
The probability of interarrival time greater than the threshold 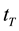 is
is
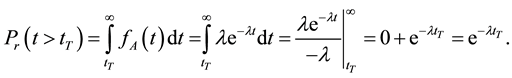 (1)
(1)
The probability of an MS to reach “sleep mode” after being failed ith times can be expressed as follows:
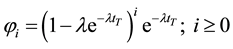 . (2)
. (2)
The mean value of interarrival time is
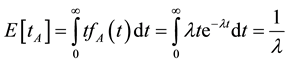 . (3)
. (3)
We also have the probability of interarrival time lower than the threshold 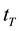 is
is
 . (4)
. (4)
If the MS fails ![]() times to reach the sleep mode, then
times to reach the sleep mode, then
![]() . (5)
. (5)
Average timer inactivity time is
![]() . (6)
. (6)
The entire analysis can be done in an alternate way as shown below. Let t is random variable of interarrival time and ![]() is another random variable indicates
is another random variable indicates![]() . So, the pdf of
. So, the pdf of ![]() is:
is:
![]() (7)
(7)
The mean value of ![]() is
is
![]() . (8)
. (8)
Therefore,
![]() . (9)
. (9)
In this paper we propose a state transition chain to represent the mode of the MS as shown in Figure 2; where three
![]()
Figure 2. Steady state transition chain of MS.
states: silent, timer inactivity and serving of buffer are taken to make consistent with the previous analysis. The probability of steady states are represented as:![]() ,
, ![]() and
and ![]() where the probability of transition among the states are shown aside the arrow in a simplified form. The closed form expression of the probabilities is derived previously.
where the probability of transition among the states are shown aside the arrow in a simplified form. The closed form expression of the probabilities is derived previously.
Applying node equations on Figure 2, we have
![]() , (10)
, (10)
![]() , (11)
, (11)
and
![]() . (12)
. (12)
Solving the above three linear equations, we obtain
![]() , (13)
, (13)
![]() , (14)
, (14)
and
![]() . (15)
. (15)
4. Results
In this section we compare the mean timer inactivity time ![]() of two methods used in this paper. Figure 3 shows the variation of mean inactivity time
of two methods used in this paper. Figure 3 shows the variation of mean inactivity time ![]() vs threshold interarrival time tT taking packet arrival rate as a parameter. Both the methods show very simial results. Figure 4 shows the variation of mean timer inactivity time
vs threshold interarrival time tT taking packet arrival rate as a parameter. Both the methods show very simial results. Figure 4 shows the variation of mean timer inactivity time ![]() against packet arrival rate. We observe from this figure that the mean timer inactivity time
against packet arrival rate. We observe from this figure that the mean timer inactivity time ![]() increases exponentially with increase in threshold interarrival time tT and packet arrival rate as is visualized from Figure 3 and Figure 4. The unit of
increases exponentially with increase in threshold interarrival time tT and packet arrival rate as is visualized from Figure 3 and Figure 4. The unit of ![]() and
and ![]() are in ms and frames/ms respectively.
are in ms and frames/ms respectively.
![]() Time’s timeout time (tT)
Time’s timeout time (tT)
Figure 3. Variation of mean activity time vs threshold interarrival time.
![]()
Figure 4. Variation of mean inactivity time vs packet arrival rate.
Figure 5 shows the profile of steady probability states of the MS against the packet arrival rate. The silent state decreases with increase in the arrival rate since the MS gets less opportunity to enter the silent state with frequent arrival of packets. Same phenomenon is true with increase in the threshold value of the interarrival time, as is also visualized from the Figure 4 for tT = 1.2 and 1.5 ms. The reverse phenomenon will happen for serving state, i.e., probability of reaching serving state will increase with increase in both “arrival of packets” and “threshold interarrival time” as is also found from the same figure. The profile of probability of timer inactivity state resembles to Gaussian shape where the probability of the state has maxima at a certain arrival rate. The maxima is found at higher arrival rate with lower “threshold interarrival time”.
Since entire results of the paper are analytical, therefore, we have used Mathcad 15.x to plot the graphs.
5. Conclusion
In this paper we propose two statistical methods to evaluate the “average timer inactivity time” in a simplified technique compared to the existing models. Both the models show very close results as shown in the previous section. Another contribution of this paper is to model the MS of IEEE802.16m based on the state transition chain of three states. Statistical model of previous literature used Laplace transform to simplify the model in the s-domain, but in this paper, we have done the entire job in time-domain. The entire work can be extended for virtual MIMO of 5G mobile communication where an additional state has to be included and may be designated as “relay state”, since an MS may be used as a relay station under a group to serve another MS.