A New Approach Based on MoM-GEC Method to Mutual Coupling Analysis of Symmetric Twin Waveguides for Antenna Applications ()
Received 30 October 2015; accepted 30 November 2015; published 3 December 2015


1. Introduction
Open-ended rectangular waveguide is the elementary component for the millimeter wave’s propagation. Several kinds of design have been proposed (single, coupled, networked...) to be used to achieve several applications such as satellite communication, radar, medical systems, and geophysical applications [1]-[3]. The variational method is the first approach used to solve the electromagnetic problem concerning these areas [4] [5]. The boundary conditions require a relationship between the tangential electromagnetic fields, which leads to an integral equation [6]. This integral equation is solved using the moment method to investigate the single or coupled waveguides behaviors.
In [7], the aperture field is modeled using the LSE modes and is based on point-matching approach. This formulation is extended in [8] by including the cross-polarized component and a dominant mode approximation is employed. Another approach consists in formulating the waveguide coupling with an iris [9] by employing orthogonal functions associated to the LSE modes. In fact, a general asymptotic formula to study the coupling between modes in separate waveguides has been applied to investigate the response of a uniform [10], and non- uniform rectangular waveguide array [11].
Some other authors have used the generalized network formulation, which is based essentially on the equivalence principle and MoM method. This formulation was applied to finite phased arrays [12] and reactively loaded waveguide arrays [13].
There are many other methods which have been applied to solve the flanged waveguide problem. The correlation matrix method which is based on the energy conservation low has been applied in [14], while Teodoridis et al. [15] have used the characteristic modes and the problem is solved by investigating the eigenvalues. In [16], Boudrant et al. have obtained an integral equation by using the operator transverse method. This integral equation was solved using the Galerkin’s method.
In [17], a rigorous formulation based on integral equation is proposed and solved by MoM method in order to analyse the radiation of rectangular waveguides array. Another approach consists to consider this last as a flanged parallel-plate waveguides array [18]. Serizawa et al. [19] used an analytical method based on Kobayashi potential method (KP) and derived the exact expressions of the fields to obtain reference data of physical quantities.
Mongiado et al. [20] proposed a singular integral equation approach including the edge condition on the apertures from the start, in order to analyze single and twin radiating waveguide
In this paper, a new rigorous approach is proposed to model two opened waveguides radiating in free space. The concept consists, firstly, in using the symmetry principle to reduce structure to half, and simulate properly the free space by another rectangular waveguide. Secondly, it consists in studying electromagnetic coupling between these waveguides. For validity purpose, obtained results are compared to those in previous works, and good agreement is shown.
2. MoM-GEC Formalism
Basically, in electromagnetic study, problems are well described by Maxwell’s equations. But in order to alleviate their complexity, we always need to choose the appropriate method that can approximate environment and boundary conditions to compute it within a reasonable time [11] [21] [22] . In our case, we combine two methods. The first method is the generalized equivalent circuits (GEC) [22] . It can present integral equations by equivalent circuit that describes faithfully all the problem. Electromagnetic phenomenon in discontinuity, which is the unknown problem, is presented by a virtual source. The environments are brought back to discontinuity plan as admittance or impedance operator. Excitation is illustrated as a localized or a modal source, in discontinuity too [23] . The second is the method of moment (MoM) [21] . It associates the known test functions to a virtual source, injects a modal basis in environment operator, and projects test function on a modal basis to resolve the problem. The good choices of test function lead to accelerate the convergence, and reduce greatly the computation time [24] .
3. Formulation
In this paper, we propose a modular formulation, in other terms, we simplify the problem step by step.
As shown in Figure 1, the study structure is composed by two opened rectangular waveguides, called network guides (NG), radiate in free space. This latter is considered as a third waveguide, called space guide (SG); with large dimensions.
In the second time, we use the symmetry principle to reduce the number of NGs to one. Then, odd and even input impedance are determined respectively when we apply structures presented in Figure 2(a) and Figure 2(b). Thus, the input impedance of initial structure is easily deduced as it will be shown later.
Finally, we propose to study the SG influence, and we will make sure that considered dimensions do not affect the results.
So, now the problem is reduced to study NG1 radiates in SG. For this, we present the new considered structure in Figure 3(a); and its relative equivalent circuit model in Figure 3(b).
The excitation is brought back to discontinuity plan as a modal source of current, its value is the current density of the fundamental mode, and its internal admittance is . This latter represents the evanescent modes contribution of NG1; and its formal writing is:
. This latter represents the evanescent modes contribution of NG1; and its formal writing is:
 (1)
(1)
where 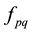 is the NG1 modal basis without the fundamental
is the NG1 modal basis without the fundamental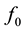 , and
, and 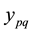 is the mode admittance of each
is the mode admittance of each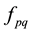 . The voltage at terminals of this source is
. The voltage at terminals of this source is , who is its dual greatness.
, who is its dual greatness.
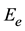 is the virtual voltage source defined in discontinuity plan, and
is the virtual voltage source defined in discontinuity plan, and 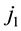 is the current flowing it.
is the current flowing it. 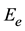 is the problem unknown, and
is the problem unknown, and  is expressed as a serial of test functions
is expressed as a serial of test functions 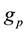 weighted by unknown modal amplitudes
weighted by unknown modal amplitudes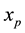 :
:
![]() (2)
(2)
The modes contribution of SG is expressed in the discontinuity plane by admittance operator ![]() .
.
![]() (3)
(3)
where ![]() is the SG modal basis and
is the SG modal basis and ![]() is the relative mode admittance.
is the relative mode admittance.
Based on the equivalent circuit shown in Figure 3(b), the integral equations associated with the problem can be easily derived by applying Kirchhoff laws generalized:
![]() (4)
(4)
Using the equations system (4), we can write:
![]() (5)
(5)
Then, we can deduce the current![]() :
:
![]() (6)
(6)
Taking into account the expression![]() , we can find the relation between source variables and their duals:
, we can find the relation between source variables and their duals:
![]() (a) (b)
(a) (b)
Figure 3. Simplified structure and the relative equivalent circuit.
![]() (7)
(7)
Applying the Galerkin’s method:
![]() (8)
(8)
This equations system can be rewritten as:
![]() (9)
(9)
where A is the excitation vector, and [y] is the admittance matrix:
![]() (10)
(10)
![]() (11)
(11)
By separating the admittance operators, we can rewrite [y] matrix as:
![]() (12)
(12)
where the first term presents the projection of test functions on the evanescent modes of the same guide, and the second term their projection on the load operator.
Finally, we deduce the unknown problem:
![]() (13)
(13)
Taking into account relations (8) and (12), we deduce the input impedance z:
![]() (14)
(14)
And scattering matrix is given by:
![]() (15)
(15)
where ![]() is impedance of free space.
is impedance of free space.
To pass to total structure, we must replace![]() , in Equation (13), by
, in Equation (13), by ![]() or
or ![]() depending on boundary conditions described in Figure 2.
depending on boundary conditions described in Figure 2.
So, the total input impedance matrix ![]() is given by:
is given by:
![]() (16)
(16)
We note that z is the reduced matrix, and ![]() is the identity matrix.
is the identity matrix.
![]() (17)
(17)
The total scattering matrix ![]() is expressed as:
is expressed as:
![]() (18)
(18)
Here, the formulation gives us ![]() parameters between NG1 and NG2; and SG has no more influence.
parameters between NG1 and NG2; and SG has no more influence.
4. Numerical Results
In this section, we propose first a quantitative discussion about the radiation of a real opened waveguide (WR90) in the free space, in order to determine the appropriate model that simulates the free space. Second, we study the electromagnetic coupling between NG1 and NG2.
To set certain parameters of the problem, a convergence study is strongly recurred. Figure 4 presents the S11 norm as a function of a mode number for different test function number.
As shown in Figure 4, the convergence is obtained for 15 test functions and 1600 mode functions. To ensure the convergence, in the following, we always use these last values.
First main target of this study is to determine the appropriate SG dimensions to simulate the free space. For this, we present in Figure 5 the S parameters as function of![]() . Where D and d1 are respectively dimensions of SG and NG1.
. Where D and d1 are respectively dimensions of SG and NG1.
We can consider that from D = 7d1 − 4.6λ there is no influence of SG on results. For a validation propose, we present in Table 1, the obtained reflection coefficient S11 and that obtained in previous works for operating frequency f = 9.33 GHz. It is found that a good agreement is shown.
The second main target of this study is to determine coupling effects between two NGs. For this we explore![]() parameter, and validate it with previous work [7] (Figure 6). We notice that a good agreement is shown around the operating frequency f = 9.33 GHz.
parameter, and validate it with previous work [7] (Figure 6). We notice that a good agreement is shown around the operating frequency f = 9.33 GHz.
We present in Figure 7, the ![]() parameter as function of the coupling distance d. And we can notice that for
parameter as function of the coupling distance d. And we can notice that for![]() , the coupling coefficient reaches a value of
, the coupling coefficient reaches a value of![]() . This coupling value corresponds to 2% of the total energy. So, from this distance, we can consider the two waveguides as isolated.
. This coupling value corresponds to 2% of the total energy. So, from this distance, we can consider the two waveguides as isolated.
At![]() , the scattering matrix
, the scattering matrix ![]() worth:
worth:
![]() (19)
(19)
![]()
Figure 4. |S11| based on mode number and at several test functions number ratio for operating frequency f = 9.33 GHz and for NG1 is a WR90 waveguide.
![]()
Figure 5. S parameters based on dimensions ratio for operating frequency f = 9.33 GHz and for NG1 is a WR90 waveguide.
![]()
Figure 6. ![]() as function of frequency for r = 10, coupling distance d = 25.4 mm, and NGs are WR90 waveguides.
as function of frequency for r = 10, coupling distance d = 25.4 mm, and NGs are WR90 waveguides.
![]()
Table 1. Comparison of reflection coefficient with published results.
We can notice that ![]() does not contain the entire energy.
does not contain the entire energy.
![]() (20)
(20)
![]()
Figure 7. ![]() parameter as function of distance d, f = 9.33 GHz, r = 10, and NGs are WR90 waveguides.
parameter as function of distance d, f = 9.33 GHz, r = 10, and NGs are WR90 waveguides.
![]()
Figure 8. Normalized electric field in discontinuity plan, r = 10, d = 2λ, f = 9.33 GHz.
If one considers the load operator ![]() which is in fact the free space, we can explain the difference by the radiating energy in the free space. This radiation is given by:
which is in fact the free space, we can explain the difference by the radiating energy in the free space. This radiation is given by:
![]() (21)
(21)
Moreover, we present the normalized electric field in the discontinuity plan, with![]() , r = 10, and we can verify that it is maximum in the radiating apertures and vanishes on the metal surface. This shows (Figure 8) that the electric field verifies the boundary conditions.
, r = 10, and we can verify that it is maximum in the radiating apertures and vanishes on the metal surface. This shows (Figure 8) that the electric field verifies the boundary conditions.
5. Conclusion
In this study, we apply a rigorous formulation based on MoM-GEC method to explore a radiation of twin open ended waveguides in the free space. The main idea is composed by two steps. First, we consider two waveguides with a simple concentric discontinuity in the propagation axis. One represents the radiating waveguide, and the other is the load waveguide; and we seek how this latter can properly simulate the free space. So, we determine its appropriate dimensions so that it no longer affects the scattering parameters. Second, we studied the electro- magnetic coupling between these two open ended waveguides and we present the electric field in the discontinuity plan. For a validation purpose, obtained results are compared to previous published works and boundary conditions are verified and a good agreement is shown. From the numerical results discussion, we can deduce that the load waveguide emulates the free space and no mismatch problem is shown from r = 7 and that the electromagnetic coupling for twin waveguides can be considered neglected from a coupling distance![]() .
.