Received 12 October 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
1.1. Ideal Economic Dispatch
The economical operation of power system needs more accurate representation of fuel cost coefficients and transmission loss coefficients. Due to changing weather conditions and other external issues, the aforesaid coefficients are not ideal and hence the existing parameters with ED solutions also change. Therefore, the objective of this article is to revise the existing parameters for the Preferred Economic Dispatch (PED) solutions.
1.2. Literature Review
Various optimization techniques have been proposed by many researchers to deal with the parameter estimation problems. To obtain the exact parameters for ED problems different parameter estimation rehearsal has been projected to solve estimation problems in power systems. State estimation based technique such as Least Error Square (LES) and least absolute value methods have been demonstrated. Among the two techniques, LES technique has been the most famous static estimation technique and in use for a long time as the preferred technique for optimum estimation of parameters. In general, some limitations and disadvantages are associated with this approach. El-Hawary and Mansour conducted performance analysis of LES, Bard algorithm, Marquardt algorithm and Powell regression algorithm for estimating coefficients [1] . The methods based on the least absolute value approximations and curve fitting techniques have been reported for fuel cost coefficients estimation [2] . Two polynomial curve fitting methods, Gram-Schmidt orthonormalization and least square are also applied to evaluate the fuel cost coefficients [3] . Further Henry Y. K. Chen and Charles E. Postel applied sequential regression technique to online parameter estimation of input-output curves for thermal units [4] .
Research endeavours indicate that the field of Transmission Line Parameters (TLP) estimation in power system studies is less focused. Traditionally, tower and conductor geometric parameters, conductor type, assumed ambient conditions etc., are utilized for estimating TLP [5] - [7] . The sending and receiving end voltage and current phasors are utilized to derive the TLP and propagation constant [8] . The synchronized phasor measurements at both ends of the transmission line emphasises the online parameter estimation [9] - [12] . Wagenaars et al., have proposed the measurement method, based on a pulse response measurement, to determine the transmission line parameters of the shield-to-phase and phase-to-phase modes [13] . Researchers have reported Newton-Raphson based method for estimating TLP parameters utilizing the measurements of voltage, current and power [14] .
A new category of classical optimization techniques has emerged to cope with some of the traditional algorithms in the field of power system estimation problems. The heuristic techniques such as Genetic Algorithm (GA) [15] , Particle Swarm Optimization (PSO) [16] [17] , Artificial Bee Colony (ABC) [18] , Artificial Neural Network (ANN) [19] [20] , Fuzzy Logic (FL) [21] , Ant Colony Optimization (ACO) [22] and Bacterial Foraging Algorithm (BFA) [23] - [25] have been used for solving various estimation problems such as load forecasting, state estimation and induction motor parameters.
1.3. Optimization Techniques
The heuristic techniques outperform the mathematical methods but their solution quality is sensitive to the algorithmic controlling parameters like population size and number of generations. Besides common control parameters, different algorithms require their own algorithm specific control parameters. Major disadvantage of ABC, PSO and GA are the presence of various parameters that need to be carefully tuned to reach acceptable estimation performance. Recently, TLBO, a nature inspired algorithm that is based on the effect of influence of a teacher on the output of learners in a class [26] [27] is proposed. It is a powerful evolutionary algorithm that maintains a population of students, where each student represents a potential solution to an optimisation problem. Each searching generation includes initializing of class, teacher phase, learner phase and termination criterion. The advantage of TLBO are simple, easy implementation and necessitates few control parameters for tuning that make it suitable to implement for power system parameter estimation problems. TLBO is an algorithm-specific, parameter-less algorithm that does not require any algorithm-specific parameters to be tuned [28] . This algorithm can find the global solution for nonlinear constrained optimization problems with less computation effort and high consistency [29] . The authors have proposed the TLBO algorithm for estimating the accurate parameters of the input output characteristics of thermal units [30] . The adaptable properties of this algorithm encourage the authors to use TLBO as a parameter estimator.
1.4. Research Gap and Motivation
The most important issue in ED problem is to have an accurate estimate of parameters. The exact ED solution in power generation and the estimation of parameters in transmission systems is an important task in power systems. The demonstration of literature review reveals that the estimation of accurate fuel cost coefficients and transmission line parameters are carried out independently. The impact of change in transmission line parameters on the loss coefficients of ED problem is seldom carried out. These points motivate us to contribute research in estimation of cost and emission coefficients, transmission line parameters and transmission loss coefficients for the exact ED solution. The TLBO algorithm is implemented for solving parameter and ED problems on different scale of test systems.
1.5. Highlights
・ Accurate parameters of different generator cost functions and transmission lines are estimated.
・ The preferred economic dispatch is carried out.
・ A 19 unit practical Indian utility system is considered.
・ A nature inspired TLBO is applied for both estimation of parameters and for solving ED problems.
1.6. Paper Organization
The rest of the paper is structured as follows: Problem formulation is explored in Section 2. Section 3 describes the implementation for preferred ED. The detailed discussions about numerical results achieved by various test systems are detailed in Section 4. Section 5 describes the potential verification of TLBO. Finally, Section 6 presents the conclusions of this article.
2. Problem Formulation
2.1. State of the Art Model
The state of the art multi objective ED model is presented as follows.
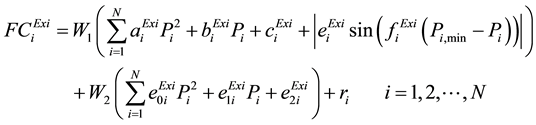 (1)
(1)
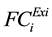 is a existing fuel cost function, N is the number of generating units and Pi is the power generated by ith generating unit.
is a existing fuel cost function, N is the number of generating units and Pi is the power generated by ith generating unit.
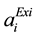 ,
, 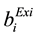 ,
, 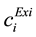 are the existing cost coefficients,
are the existing cost coefficients, 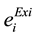 ,
,  are the existing valve point coefficients and
are the existing valve point coefficients and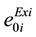 ,
, 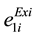 ,
, 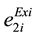 are the existing emission coefficients .
are the existing emission coefficients .
W1 and W2 are the weights of the function.
ri is the error associated with the ith equation.
Loss function: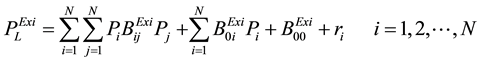 (2)
(2)
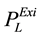 indicates existing transmission loss.
indicates existing transmission loss.
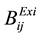 ,
, 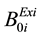 ,
, 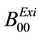 are the existing transmission loss coefficients.
are the existing transmission loss coefficients.
2.2. Proposed Parameter Estimation Problems
For preferred ED solution, the accurate parameters for fuel cost, emission, and transmission line and transmission loss are needed. Those parameters can be estimated by solving the following problems.
Cost coefficients Estimation, FCEst = Estimate [a, b, c, e, f]
Emission coefficients Estimation, EEst = Estimate [e0, e1, e2]
Transmission line parameters Estimation, TLPEst = Estimate [R, X, B]
Transmission loss coefficients Estimation, KCEst = Estimate [Bij, B0i, B00]
In general to estimate the accurate parameters, the following function are used
![]() (3)
(3)
2.3. Accurate Model Using Estimated Parameters
The cost function of generating unit is expressed using estimated coefficients as follows,
![]() (4)
(4)
where ![]() is an estimated fuel cost.
is an estimated fuel cost.
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the estimated cost coefficients, valve point coefficients and emission coefficients respectively.
are the estimated cost coefficients, valve point coefficients and emission coefficients respectively.
Loss function:![]() (5)
(5)
![]() ,
, ![]() ,
, ![]() are the estimated transmission loss coefficients and
are the estimated transmission loss coefficients and ![]() is the estimated transmission loss.
is the estimated transmission loss.
2.4. Error Minimization
As detailed in [30] , the error is estimated for fuel cost and emission coefficients as follows
The error at each step i can be calculated as,
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
The % error for each step k of transmission line parameter is expressed as,
![]() (9)
(9)
The objective function is minimised subjected to physical limits of each coefficients and TLP.
3. Implementation of TLBO for Preferred Economic Dispatch (PED)
This section details the computational flows for parameter estimation and PED problems.
3.1. Parameter Estimation Procedure
Step 1: Read the required data for estimating the parameters, population size, maximum number of iterations (Itermax), maximum and minimum limits of parameters (PAmin,![]() ).
).
Step 2:Randomly generate parameters using the following equation,
![]() (10)
(10)
Step 3: Check for the constraint violation.
Step 4: If the limit is violated, then upgrade the parameters of the units using the following equation
![]() (11)
(11)
Step 5: Calculate FCEst by using Equations (4).
Step 6: The error and % error associated with each measurement can be calculated by using Equations (6), (7), (8) and (9).
Step 7: Teacher phase: Compute the difference between existing mean result and best mean by utilizing teaching factor![]() .
.
Step 8: Learner phase: Evaluate the learners’ parameter values with the help of teacher’s parameter values.
Step 9: Update the parameters subject to constraints.
Step 10: Stopping Criterion: If Iter ≥ Itermax print the optimal results, otherwise go to step 7.
3.2. Computational Flow of PED
Hence the estimated parameters are suitably achieved. The ED solution is carried out and the computational flow is as follows in Figure 1.
4. Numerical Simulation Results and Discussion
This section presents three different test systems such as 10 unit, IEEE 30 bus and a practical Indian Utility system to demonstrate the efficacy of the proposed solution technique for perfect estimate of parameters and preferred ED solutions. The algorithm is implemented in Matlab package and simulations are carried out on a personal computer having the configuration of Intel(R) core i3 CPU with 2 GB RAM. The following algorithmic parameters are chosen for all cases in order to validate the performance of the algorithm: Population size = 10;
![]()
Figure 1. Flowchart for preferred economic dispatch using TLBO.
Maximum number of iterations = 120.
4.1. Test System 1: 10 Unit System with Piecewise Quadratic Functions
This test system consists of 10-generating units in which each unit has two or three fuel options like coal, oil and gas. As more than one fuel is used, the generator input-output characteristic is expressed as a piecewise quadratic function. The valve point effects are also considered. The test system data is available in [31] .
The generator characteristic is expressed as a piecewise quadratic function including valve point effects increases the number of variables to be estimated. In this test system, the generator 1 has two fuel options and the remaining units have three fuel options. It is specified that the fuel 2 is uneconomical for generator 9. The simulation is carried out using the proposed TLBO which acquires new values for cost coefficients and are presented in the Table 1. The estimation process has been performed for each generation level and the results of existing
![]()
Table 1. Estimation of piecewise quadratic cost function coefficients using TLBO-10 unit system.
fuel cost (FCExi) and estimated fuel cost (FCEst) are presented independently for each fuel type in the Table 1. The error is also computed by comparing FCExi and FCEst using Equation (6). The obtained error using the proposed algorithm is compared with ABC algorithm which clearly illustrates the superiority of TLBO over other algorithm.
The ED is carried out separately considering both existing and estimated fuel cost coefficients. The obtained results for various demands are presented in Table 2 along with % error, which clearly illustrates the impact of estimated coefficients on ED problem.
4.2. Test System 2: IEEE 30 Bus System
The TLBO algorithm has been executed on the test system consists of six generating units interconnected with 41 branches of transmission lines. Generator data, emission characteristics and line data are obtained from [32] . TLBO algorithm is applied to estimate the cost, emission coefficients and transmission line parameters. For each unit, the fuel cost and emission coefficients are computed. Table 3 and Table 4 show the TLBO outcomes of the
![]()
Table 2. Economic dispatch with improved parameters for 10 unit system.
![]()
Table 3. Estimation of quadratic cost function coefficients by TLBO-IEEE 30 bus system.
![]()
Table 4. Estimation of emission function coefficients by TLBO-IEEE 30 bus system.
estimated coefficients. Existing fuel cost and existing emission for three different power generations are compared with its FCEst and EEst and it is found that those values are very close to each other. The new values of coefficients and their related total error are presented in the Table 3 and Table 4. From the results the error obtained by TLBO for all specified output of generating units is less which shows the accurate estimation of the system parameters.
TLP are obtained using Equations (A.2-A.5) for each line and the estimated TLP results are listed in Table 5. The estimated TLP values are compared with base case values and the percentage error is computed using Equation (9). The % error values for transmission lines are almost close to zero except for the lines 24 and 29 for which the TLP values are above 1. The efficiency of transmission lines 11-16, 37 are high as compared to other transmission lines, due to the presence of three winding transformer in the transmission lines. The estimated R, X, B values for each transmission line are presented in Table 5. The estimated transmission loss coefficients using Equations (A.10-A.11) are detailed in the Table 6.
By using existing parameters, economic emission dispatch is carried out and the results are listed in Table 7. The dispatch results are obtained for three different load demands of 275 MW, 284.4 MW and 300 MW. With the new estimated parameters for fuel cost function, emission and loss, the multi-objective ED problem is solved and the results are compared with the existing results. From the results, the percentage deviation of fuel cost, emission and network loss for estimated parameters are slightly elevated as compared to the existing parameters. The % error of all these values reveals the impact of accurate parameter estimation for ED problems.
4.3. Test System 3: 62 Bus Indian Utility System
In this case, a 62 bus Indian utility system is considered for estimating the improved parameters by using the proposed algorithm. The chosen test system consists of nineteen power producers, eighty nine (220KV) lines
![]()
Table 5. Estimation of transmission line parameters for IEEE 30 bus system (in p.u).
nl: start bus of a line; nr: end bus of a line; Re, Xe and Be: Errors in TLP.
![]()
Table 6. Estimated B-Coefficients for IEEE 30 bus system.
![]()
Table 7. Economic emission dispatch with improved parameters for IEEE 30 unit system.
with eleven tap changing transformers. The bus, line and generator data of the test system are taken from [32] .
The proposed method of determining the improved parameters is applied for the chosen test system and the obtained results are listed in Table 8. For each unit the fuel costs using improved parameters for three different real power outputs are also specified. In comparison with base case values the error is calculated for each generating unit. The obtained error is small which reveals that the estimation of the coefficient is accurate.
Further the estimation of TLP is carried out using A.2-A.5. The obtained TLP values by TLBO algorithm are listed in Table 9. The % error values for each transmission line are close to zero, except for few lines, which shows that the obtained TLP values are accurate. With the improved TLP values, the transmission line efficiency is calculated and is listed in Table 9. It is also inferred from Table 9 that the efficiency of each transmission line obtained using TLBO is nearly the same as compared to the base case.
The PED is carried out with improved cost coefficients of generators and improved TLP for three different load demands of 2900 MW, 2967 MW, 3200 MW are obtained and the results are presented in Table 10. The estimated transmission loss coefficients using Equations (A.10-A.11) are presented in the Table 11. The results obtained are compared with the existing fuel cost and loss and the % deviation of fuel cost and transmission loss is computed and presented. The obtained results clearly illustrate the impact of improved parameters on ED problem.
5. Potential Verification of TLBO
5.1. Solution Quality
Using the proposed algorithm several runs have been carried out by varying the population size.In this analysis there is no larger difference in the average fitness value above the population size of 10. Hence the population size of 10 is preferred for all estimation process. The simulations are performed to estimate the quadratic cost function coefficients, piecewise quadratic valve point coefficients, emission coefficients, transmission line parameters and transmission loss coefficients using three different test cases. For these cases the existing coefficients at the time of installation are only available, hence the obtained improved parameters are compared with only these values. From the obtained simulation results, the cost coefficients, emission coefficients and transmission line parameters are very close to the existing values and are presented in Tables 2-6 and Tables 8-10. The comparisons of total error in each case clearly indicate that the proposed method provides the best estimate of accurate coefficients.
![]()
![]()
Table 8. Estimation of quadratic cost function coefficients using TLBO?62 Bus systems.
5.2. Statistical Analysis
The reliability of the algorithm in finding the best solution can be viewed by performing statistical analysis. The convergence property and the robustness characteristics are focused primly for the statistical analysis. The standard statistical parameters of the objective functions such as best, worst and average values in addition to standard deviation and solution iter are also worked out and analyzed and are given in Table 12. The standard deviation value is small which indicates the accuracy of estimate.
Convergence: The TLBO algorithm is implemented on different scale of test systems and for all cases, the convergence characteristics are plotted. The convergence pattern illustrates the searching ability of algorithm.
Figure 2 shows the convergence characteristics of 10 unit multiple fuels system; the proposed approach converged to a good solution within the 50 iterations for the three different fuels. For the IEEE 30 bus and 62 bus Indian utility systems, the convergence graphs are shown in Figure 3. Figure 2 and Figure 3 show that the TLBO has good convergence property, thus resulting in good evaluation value and low error.
Robustness: Many trials with different initial population have been carried out to test the consistency of the TLBO algorithm. The algorithm is executed for 50 trials and the obtained objective function values are presented in Figure 4. The mean value is close to the optimal value for all the cases. This description clears that the TLBO provides great searching ability, higher solution quality and the best estimate.
5.3. Observations
・ Accurate parameters are estimated for three different test systems involving a practical test system.
・ For the first time in the literature, both the parameter estimation and economic dispatch are carried out
![]()
![]()
![]()
Table 9. Enhanced parameters for Indian Utility 62 Bus system (in p.u).
![]()
Figure 2. Cost coefficients convergence curve (a) fuel 1; (b) fuel 2 and (c) fuel 3.
![]()
Figure 3. Convergence curve: (a) IEEE 30 bus cost coefficients; (b) IEEE 30 bus emission coefficients; (c) 62 bus cost coefficients.
![]()
Table 10. Economic dispatch with improved parameters for Indian utility 62 bus system.
concurrently.
・ The % error estimation of parameters reveals the rate of change in parameters over the years due to physical conditions like aging.
・ The results clearly signify the impact of accurate parameters on ED problems on fetching the accurate dispatch results over existing results.
6. Conclusion
In this paper, the TLBO algorithm is successfully implemented for both the operation of parameter estimations and ED solution. The operational aspects of the generators such as valve-point loading, emission, multiple fuel options and transmission loss are considered. The three different test systems involving a practical test system are selected for this estimation and dispatch problem. The results obtained by satisfying all the constraints for all cases by the proposed algorithm are always comparable or better than the other methods. It is revealed that the
![]()
Table 11.Estimated B-Coefficients for 19 unti Indian utility system.
![]()
![]()
Figure 4. Robustness characteristics: (a) 10 unit system for fuel 1; (b) 10 unit system for fuel 2; (c) 10 unit system for fuel 3; (d) IEEE 30 bus system for cost function; (e) IEEE 30 bus system for emission function; (f) 62 bus system for cost function.
![]()
![]()
Table 12. Performance indices by TLBO for various test systems.
TLBO possesses better convergence characteristics and robustness. The proposed TLBO approach has shown merits such as better results, easy implementation for the accurate parameter estimation for PED problems. It can be concluded that the estimated parameters obtained show that the proposed method can be used as a very accurate tool for estimating the fuel cost, emission and loss coefficients.
Acknowledgements
The authors gratefully acknowledge the authorities of Annamalai University, Annamalai Nagar, Tamilnadu, India for the facilities provided to carry out this research work.
Appendix
Parameter Estimation Problems
The vector equation describing the relationships between the measured values y, the unknown parameters m, the system matrix D and the residual due to the change in values r are as follows,
![]() (A.1)
(A.1)
The parameter estimation problem for estimating the cost coefficients a, b, c, e, f, emission coefficients e0, e1, e2 and long line transmission parameters R, X, B are formulated as follows:
Let, k-Number of measurements, y(k)-Measured value of the kth measurement, D-System matrix
![]()
r-Error vector that relates y(k) to m.
There are k equations available to represent the parameter estimation that forms measurement matrix y(k).
TLBO is used as an estimator to find the unknown values of [m]. These estimates are used to recalculate parameters using consequent equations at each time step. The calculation procedure for the evaluation of parameters such as a, b, c, e, f; e0, e1, e2 and Bij, B0i, B00are detailed in Section 2.2, and the transmission line parameters such as R, X, B are presented in (A.2-A.5).
![]() (A.2)
(A.2)
![]() (A.3)
(A.3)
![]() (A.4)
(A.4)
![]() (A.5)
(A.5)
Next, using the Newton-Raphson (NR) method, the following four non-linear equations of the form F(x) = 0,
where ![]() and
and ![]() are solved for the unknown X, R, B,
are solved for the unknown X, R, B,
![]() (A.6)
(A.6)
![]() (A.7)
(A.7)
![]() (A.8)
(A.8)
![]() (A.9)
(A.9)
Transmission Line Loss Parameters
The network loss is a function of transmission line parameters and network configurations. Thus accuracy in the transmission line model and B coefficients are necessary. The transmission line model consists of R, X and B parameters and to determine the existing network loss these parameters must be accurate. The estimation of transmission line parameters is mathematically formulated as an optimization problem (Indulkar and Ramalingam, 2008) and the accurate TLP can be determined by using an optimization technique.
![]() (A.10)
(A.10)
![]() are the estimated transmission line parameters
are the estimated transmission line parameters
The Kron’s coefficients (![]() ,
,![]() and
and![]() ) are dependent of network parameters and configuration.
) are dependent of network parameters and configuration.
![]() (A.11)
(A.11)
![]() ―Estimated loss coefficients
―Estimated loss coefficients
The ideal transmission loss can be determined using ![]() by Equation (5).
by Equation (5).