Analysis of the 2007-2008 Writer’s Guild Strike with Game Theory ()
Received 10 September 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
In mathematics, you don’t understand things. You just get used to them.
―Johann von Neumann
1.1. Writer’s Guild Strike
In 2007-2008 the Writer’s Guild of America went on strike. This strike lasted from November 5, 2007 until February 12, 2008. The strike itself sought to obtain increased funding from the larger studios, the management, huge profit. The 12,000 members of the TV screenwriters and writers went on strike against the Alliance of Motion Pictures and television Producers (AoMPTP), which was a trade organization that represented interest of about 397 American film and TV producers [1] . According to analysts,
“At the resolution of the strike, the writers achieved a qualified success: they received a new percentage payment on the distributor’s gross for digital distribution, they emerged united, but they lost out on short-term deals” [2] .
“WGA members argued that a writer’s residuals are a necessary part of a writer’s income that is typically relied upon during periods of unemployment common in the writing industry. The WGA requested a doubling of the residual rate for DVD sales, which would result in a residual of 0.6% (up from 0.3%) per DVD sold.” [3] .
Let’s assume the average TV DVD sells for $10.00. The request for an increase meant that the writers wanted to receive 0.6% instead of 0.3%. This amounts to an increase in $0.03 from $0.03 to $0.06 per sale [1] .
The last such strike by the writers in 1988 lasted 21 weeks and 6 days, costing the American entertainment industry an estimated $500 million ($870 million in 2007 dollars) [1] . This strike was just as devastating.
According to a report on the January 13, 2008 edition of NBC Nightly News if one takes into account everyone affected by the current strike, the strike has cost the industry $1 billion so far; this is a combination of lost wages to cast and crew members of television and film productions and payments for services provided by janitorial services, caterers, prop and costume rental companies, and the like [1] .
The TV and movie companies stockpiled “output” so that they could possibly outlast the strike rather than work to meet the demands of the writer’s and avoid the strike [1] . From the standpoint of a consumer, the consumers were also not happy.
In this paper, we develop the possible strategies for both the writer’s guild and the management. Since ne real data is available for the players, we must use utility theory to obtain values to use in the payoff matrix. We use ordinal ranking to obtain initial values to use in a game theory payoff matrix. We then utilize the alternative method described by Fox [4] to obtain cardinal utility values. Cardinal values must be used if we are to use any mathematics to calculate equilibriums or arbitration values. We examine the solution techniques for game theory by finding the Nash equilibrium, discussing why the writers are still unhappy, thus forcing the negotiation that led to the Nash arbitration.
1.2. Game Theory
Conflict is as ancient as humankind. Professionals spend a great deal of time studying the nature of conflict, and for that reason, our students in defense analysis study modeling courses sequence that allow them to use mathematical apparatus in social settings.
Models of conflict assume rational decision-maker, trying to maximize some payoffs. In game theory, the term rationality has a different meaning than most people think. Rationality does not mean what we think is best or wise; to be rational, actors have to be able a) to define their objectives, however foolish they appear to others. They have to be able b) to formulate sufficiently different alternative strategies, and c) to choose a strategy that maximizes their objective. So the question then becomes: “what should/will the rational value maximizing player do?”
In this case, we recognize that both sides need to gain something concluding this is not a zero-sum game. Thus our approach is using partial conflict game theory.
2. Game Theory Approach
Let us begin by stating strategies for each player. Our players will be the Writer’s Guild and the Management.
2.1. Strategies
Writer’s Guild: Their strategies are to strike (S) or not to strike (NS).
Management: Salary Increase plus revenue sharing as the writer’s requested (IN), revenue sharing from DVDs only at a rate of 0.6%, (GIN) revenue sharing at a substantially smaller rate (RIN) or status quo (SQ).
We will the alternative method shown by Fox (2015) in order to create cardinal utilities for the payoff matrix. First, we rank order the outcomes for each side in order of preference. These are the ordinal utilities.
First, we list the combinations of strategies that can be played in this game. This will be a 2 x 4 game. We also assume that this is a partial conflict (non-zero sum) game. We will refer to NS as R1 S as R2, SQ as C1, In as C2, RIN as C3, and Gin as C4.
NS SQ à R1C1
NS IN à R1C2
NS GIN à R1C3
NS RIN à R1C4
S SQ à R2C1
SIN à R2C2
S RIN à R2C3
S GIN à R2C4
2.2. Writer’s Alternatives and Rankings
The writers’ have 8 strategy combinations to rank. We start by ranking from Best to Worst. The writer’s prefer getting compensation to not getting any compensation.
NS IN à R1C2 = 8
NS GIN à R1C3 = 7
NS RIN à R1C4 = 6
SIN à R2C2 = 5
S RIN à R2C3 = 4
S GIN à R2C4 = 3
NS SQ à R1C1 = 2
S SQ à R2C1 = 1
2.3. Management’s Alternatives and Rankings
The management prefers not to give additional compensation but if they have to they would prefer at the lower amount. Thus, managements’ ordinal ranking might be as follows:
NS SQ à R1C1 = 8
S SQ à R2C1 = 7
NS RIN à R1C4 = 6
S RIN à R2C3 = 5
NS GIN à R1C3 = 4
S GIN à R2C4 = 3
NS IN à R1C2 = 2
SIN à R2C2 = 1
Payoff Matrix (ordinal)
A movement diagram to find a pure strategy equilibrium (see Straffin, [5] ). The pure strategy using the ordinal values is R1C1 which represents no strike and status quo. The management is quite happy and the writers are very unhappy. As a matter of fact the writers begin to consider to strike.
In order to continue the analysis with some accuracy, we need to convert the ordinal values into cardinal values. We could either use the lottery range using the Method of von Neumann and Morgenstern [6] (2004) as described by Straffin [5] or the Analytical Hierarchy Process (AHP) method described by Fox [4] . We illustrate the method described by Fox within this analysis.
We began with analyzing the writer’s strategies versus the management strategies to obtain the ordinal ranking. Now we use Saaty’s [7] 9 point scale to add utility value to those ordinal rankings. We show the pairwise comparison in Table 1.
We used an Excel template to input our 1 - 9 values, develop the matrix, and to compute the weights which will be our utility values. These can be viewed in Figure 1.
The AHP showsthat the matrix, Figure 2, that is generated is consistent as the CR = 0.00073.
The output, the eigenvectors, are the cardinal values for our strategies. These are found for the writers:
![]()
Table 1. Pair wise comparison in this order using the 9 point scale of importance. Scale for Decision-Criterion & Weights.
![]()
Figure 1. AHP inputs for the writer’s guild.
We repeat the identical process for the management. The pairwise comparisons template is shown in Figure 3 and the matrix in Figure 4.
The output eigenvector, the cardinal values, for our strategies for the management are:
![]()
Figure 2. Pairwise comparison matrix for writers.
![]()
Figure 3. AHP inputs for the management.
This provides us with a payoff matrix consisting of cardinal utilities, Table 2. This use of cardinal utilities is important because we really cannot do any mathematics (addition, subtraction, multiplication, or division) with ordinal values. Cardinal values will allow us to compute, as necessary. This will allow us to employ the cardinal values in the Nash Arbitration scheme or employ them to see if any mixed strategy Nash equilibrium exists.
Nash [8] proved that every two-person game has at least one equilibrium either in Pure or in mixed (equalizing) strategies. The equilibriums are also called Nash Equilibriums. He also developed the Nash arbitration [9] method which was use in this analysis.
2.4. Finding the Nash Equilibrium
For games with two players and more than two strategies each, we present the nonlinear optimization approach by Barron [10] . Consider a two person game with a payoff matrix as before. Let’s separate the payoff matrix into two matrices M and N for players I and II. We solve the following nonlinear optimization formulation in expanded form, in Equation (1).
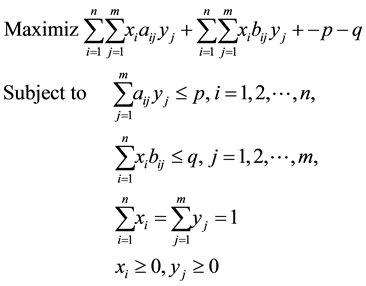 (1)
(1)
We used the computer algebra system Maple to input the game and then solve. We let the matrix aij be labeled M and bij be labeled N in Maple. We wrote a short macro to perform the work.
The commands in Maple are;
![]()
Figure 4. Pairwise comparison matrix for management.
![]()
Table 2. Payoff matrix for the game with cardinal values.
With (LinearAlgerba): with (Optimization)
A := Matrix([[0.0356, 0.02976], [0.38079, 0.091], [[0.222, 0.0619], [0.135, 0.0444]]);
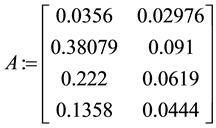
B := Matrix([[0.426, 0.0309], [0.0375, 0.03098], [0.0619, 0.0807], [[0.1167, 0.04651]]);
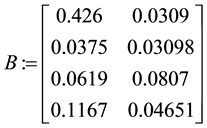
M:= Transpose(A): N := Transpose(B):
X := ‘<,>’ (x[1], x[2]): Y := ‘<,>’ (y[1], y[2], y[3], y[4]):
c1 := seq(Transpose(X). N([j] < q, j = 1..4):
c2 := seq(M.Y) [j] < p, j = 1..2):
c3 := add(x[j], j = 1..2) = 1:
c4 := add(y[j], j = 1..4) = 1:
const := {c1, c2, c3, c4};
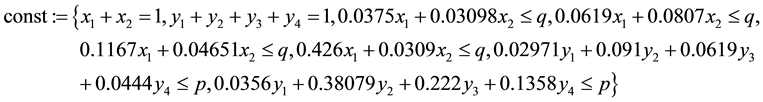
objective := expand (Transpose(X).M.Y + Transpose(X).N.Y-p-q);

QPSolve (objective, const, assume = nonnegative, maximize, iterationlimit = 1000);
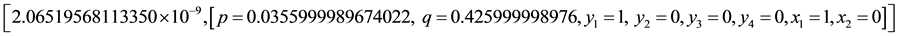
QPSolve (objective, const, assume = nonnegative, maximize, intialpoint = {p = 0.07, q = 0.59});
![]()
The Nash equilibrium, as expected is still (0.0356, 0.426) at R1C1. Changing the initial points did not uncover any additional equalizing strategy equilibriums. We also note that this result is not satisfying to the Writer’s Guild and that they would like to have a better outcome.
We define the following terms:
Pareto Principle: “To be acceptable as a solution of the game, an outcome should be Pareto Optimal”from Straffin [5] .
Pareto Optimal: The outcome where neither player can improve payoff without hurting (decreasing the payoff) the other player.
As in this case, group rationality (Pareto) is sometimes in conflict with the individual rationality (dominant). The eventual outcome depends on the players. Obtaining a Pareto optimal outcome usually requires some sort of communication and cooperation among the players.
With the assumption that the outcome should be Pareto optimal, the next question is, “What is Pareto optimal, and what is it not (Pareto inferior)?” The simplest way for this to be understood is to draw a payoff polygon of the game. On the chart, the X-axis depicts the payoffs of Rose and the Y-axis depicts the payoffs of Colin. By plotting the pure strategy solutions on the chart, one can see that the convex (everything inside) polygon enclosing the pure strategy solutions is then payoff polygon or the feasible region. Therefore, the points inside the polygon are the possible solutions of the game.
Using Excel, we plot these coordinates from the payoff matrix to determine if any points are Pareto Optimal. This is the payoff polygon, Figure 5.
The Nash equilibrium at (0.0356, 0.426), lies along the Pareto Optimal line segment. The writers’ are still unhappy with the result of this equilibrium. But the writers can do better by going on strike and forcing arbitration. This is exactly what the writer’s did, they went on strike in order to obtain a better payoff.
We can employ several options to try to secure a better outcome for the Writers’. We can first try Strategic Moves and then move to Nash Arbitration if the Strategic Moves did not provide the desired outcomes. Both of these methods employ communications in the game. In strategic moves, we examine game to see if “moving first” changes the outcome, if threatening our opponent changing the outcome, making promises to our opponent changes our outcome, or a combination of threats and promises in order to change the outcome.
The result of Strategic Moves is that 1) moving first, 2) Promises, 3) Threats, nor 4) Combination of Threats and Promises did not improve the outcome from the Nash equilibrium value of (0.0356, 0.426). The writers have no alternative but to act first and strike to force management’s hand. We move on to Nash Arbitration.
3. Nash Arbitration Scheme
“If SQ(status quo) = (x0, y0), then the arbitrated solution point N is the point (x, y) in the polygon with x ≥ x0 and y ≥ y0 which maximizes the product (x − x0) *(y − y0)” from Straffin [5] .
Status quo point in the definition is the likely outcome of the game when the negotiation fails. An arbitrated solution should be better for both players than the status quo; this is incorporated in the definition by x ≥ x0 and y ≥ y0. Status quo is the minimum the players can get. Everything above is improvement of their gain. The solution has to maximize their joint utility. The objective function ? (x − x0) *(y − y0), maximizes these ‘above security level’ utilities. In other words, it has to maximize the area of the rectangle [5] .
The status quo point can be either the security levels of each side or the threat level. We find these values using prudential strategies. Again, the software can assist us in finding these values as R1C1 at (0.0356, 0.426). The security levels do not help the writers so the move on to use the threat level (0.0297, 0.0309). Figure 6, shows the feasible region and the level curves z = (x − 0.0297) *(y − 0.0309). From the figure we can see the approximate Nash arbitration point. We will use non-linear optimization to find the Nash arbitration point [11] [12] .
4. Results
We use Maple and find the results.The Nash Arbitrated solution is (0.223, 0.24845). The Writer’s Guild should be able to improve their outcome from an equilibrium outcome of 0.0356 to 0.223 with an arbitrated solution.
F := (x − 0.02976) − (y − 0.0309):
constf := {y + 1.12547∙ x ≤ (1.12547∙ 0.03580 0.46), y > 0.0309}:
NLPSolve(f, constf, maximize);
![]()
Figure 6. Nash arbitration plot for the writers guild.
[0.0422061285219754515, [x = 0.223411469519401, y = 0.2488489400]]
How is this accomplished? In the broader sense the end points of the Pareto optimal line segment are at the northern most point most favorable to management and the eastern most point most favorable to the writers. Arbitration is a give and take process. In a mathematical sense, the arbitrators should play a mix of (0.0356, 0.426) at R1C1and (0.38079, 0.0375) at R1C2 as these points are the end points of the Pareto optimal line segment. We see clearly that the writers maintain playing R1 always and management plays a mix of C1 and C2 during the process. We find the players should be offing 45.7% R1C1 and 54.3% R2C1 to obtain this Nash arbitration point. The Nash arbitration value is the fairest value that the writers can achieve through the strike.
5. Conclusions
The worst that can happen in the negotiation is to come out at the security level or threat level. For the Writer’s Guild if the threat is indeed successful will most likely move to (0.1358, 0.1167) and this solution is certainly better for the writers than the Nash equilibrium value. The Nash Arbitrated solution is (0.2057, 0.24845) and is better for both parties. We found that using the threat level instead of the security levels achieved much better results. This is indeed a better result for the writers, which is what they desired to achieve in a long term strategy.
The analysis provides insights into the mechanics of the game between the writers and the management. Having a model allows for “what if” analysis to occur in any future negotiations.
We point out in the short run, the weeks that the writers were on strike, that lost wages and opportunity losses did occur and for management losses also occurred in viewers and sponsorship.
The true results of the strike said that the writers were able to get a new contract that gave them about 0.6% compensation for the DVDs that were sold as stated previously. As a matter of fact, the writers had to go to court to actually force management to pay this amount to them.