Decoupling the Electrical and Entropic Contributions to Energy Transfer from Infrared Radiation to a Power Generator ()
1. Introduction
A power generator (PG) device can be used to harvest electromagnetic (EM) and, in particular, infrared (IR) radiation. The interaction between the radiation and the device is a complex phenomenon of energy transfer (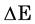
). The rate of energy transferred from the EM radiation per area a of the device is the Poynting vector 
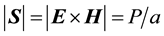, where 
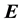and 
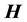are the electric and magnetic fields, respectively, and P is power. Therefore, because of 
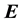and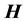 
, the interaction between radiation and device involves the charges on the device surface. Electromagnetic radiation with large frequency 
interacts through, e.g., Compton scattering [1], X-ray photoelectron effect [2], photoelectric effect [3], photovoltaic effect [4], and plasmon generation [5]. Electromagnetic radiation with low frequency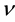 
, e.g. in the IR and microwave regions, resonates with molecular rotation and oscillation frequencies [6] or generates polaritons [7]-[10]. When the photon frequency 
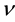or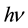
energy , where h is Planck’s constant, do not match with the frequency or the energy of a specific phenomenon involving charges, the energy of the EM radiation contributes to temperature T changes. In photosynthesis this phenomenon is known as internal conversion [11].
We name the energy transferred from the EM radiation to a PG device through the action of the electric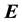 
and 
magnetic fields as the electric contribution:
, (1)
where q is the charge and V voltage. We name the energy transferred through changes in temperature T at entropy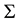 
as the entropic contribution:
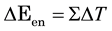. (2)
The energy transferred from IR and microwave radiation is usually associated with the entropic contribution in Equation (2). For example, sun light gives the sensation of temperature increase, and therefore of warmth, on human skin. The microwave radiation in microwave ovens is used to increase the temperature, i.e., cook food and heat-up beverages. Similarly, through laser radiation it is possible to increase temperature, even with nanoscale control [12].
The effects of the electric contribution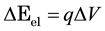 
are less apparent in the energy transfer from low frequency and low power EM radiation. In the current literature, the existence of the electric contribution is acknowledged [13]-[16], but the interplay between the electric and the entropic contributions is not investigated. Specifically, there is a lack of knowledge of 1) the possibility of decoupling the electric from the entropic contributions, 2) the factors that promote the electric over the entropic contribution, or vice-versa, 3) the existence of a threshold where one contribution prevails over the other, and 4) the benefits of the electric over the entropic contributions, or vice-versa.
In this work we aim at decoupling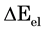 
and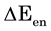 
in a PG device illuminated by low power IR radiation. The device is expected to respond to the entropic contribution by exploiting the Seebeck effect [17]-[20], i.e. producing a voltage difference 
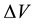directly proportional to the temperature difference 
applied to the two faces of the PG device, so that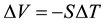 
. Here, S is the Seebeck coefficient. On the other hand, we expect the PG device to also respond to the electric contribution through its capacitor-type of structure consisting of a sequence of conducting and insulating layers, as illustrated in Figure 1. For the device used in this work, the sequence is, starting from the face illuminated by the IR radiation, a copper (Cu) plate, a layer of pillars made of adoped Bi2Te3-based alloy, another Cu plate, and, finally, an alumina (AlO) plate. On the Cu plates there are electrons whose surface density 
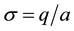is sensitive to the 
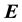and 
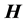fields of the IR radiation, thus enabling changes in the electric contribution 
.
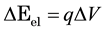In our experiment, the voltage difference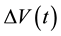 
, generated by the PG device through the electric and the entropic contributions, and the temperature difference 
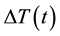, related to the entropic contribution, are observed as a function of time t. The measurements capture the first minutes after starting the illumination, and in the 30 hours thereafter. We hypothesize that changes in 
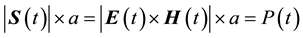slowly vary the amplitude of the surface electron density 
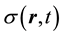. To prove this hypothesis, we study the power 
of the IR radiation using a power-meter sensor and compare its behavior with that of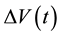 
and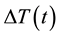 
.
Summarizing, we consider the total energy transfer in time from the IR radiation to a PG device as the sum of the electric and the entropic contributions such that:
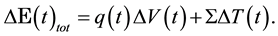(3)
![]()
Figure 1.Schematics of the away (a) and toward (b) architectures of the PG device. In the away architecture (a) the face of the PG device exposed to the IR radiation is free from contact with the sample holder. In the toward architecture (b), the il-luminated face is in contact with the sample holder. The PG device is a stack of conducting (Cu plates), non-conducting (AlO plate), and semiconducting (set of pillars made of a doped Bi2Te3-based alloy) layers.
Consequently, we assume the voltage difference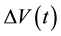 
produced by the PG device in time to be the addition of two summands:
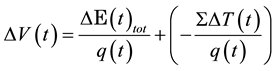. (4)
The first summand relates to the electric and the second to the entropic contribution. The term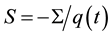 
can be associated with the Seebeck coefficient.
We will show that with the low power irradiation employed in our measurements, the electric contribution can be decoupled from the entropic contribution, and largely dominates. Decoupling the two contributions is important for IR energy harvesting, because the electric contribution offers a variety of ways to increase the voltage produced by the PG device, e.g. by placing black-colored gaffer tape on the illuminated face of the device, as we will show in Appendix-1. The entropic contribution, instead, is limited by the temperature difference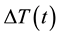 
established between the two faces of the PG device.
2. Experimental Set-Up
For this experiment, continuous broadband IR radiation in the middle IR (MIR) region (i.e. frequency between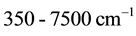 
, or wavelength between 
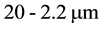) was produced by a globar (Q301) source. The power 
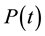of the IR radiation was monitored versus time using a power-meter sensor Coherent Power Max RS PS19, sensitive to the 
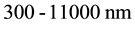wavelength range, and to the 100 μW to 1 W power range.
The voltage difference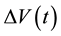 
, generated by the electric and the entropic contributions to 
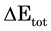according to Equation (4), was produced using a PG device 07111-9L31-04B by Custom Thermoelectric Inc. The device consists of a sequence of layers: 1) a Cu plate on the face exposed to the IR radiation, 2) a layer of pillars made of a doped Bi2Te3-based alloy, 3) another Cu plate, and 4) an AlO plate. The Cu plate not illuminated by the IR radiation is non-continuous, as highlighted through the white hole in the left side of Figure 1(a) and Figure 1(b). In the away architecture, illustrated in Figure 1(a), we established the continuity by placing the sample holders, made of anodized aluminum, in contact with the non-continuous Cu plate. Thus, the Cu plate together with the sample holder behaves as the electrode of a capacitor. The illuminated Cu plate, instead, was free of contact with the sample holder. In the toward architecture, pictured in Figure 1(b), we left non-continuous the Cu plate opposite to the IR radiation, while the illuminated Cu plate was kept in contact with the sample holder.
The temperatures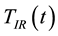 
and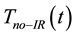 
of the illuminated and non-illuminated faces, respectively, of the PG device were measured using OMEGA type E Ni-Cr/Cu-Ni thermocouple probes. The temperature difference 
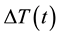was obtained as 
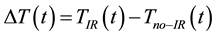. The trends of 
, 
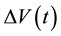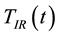and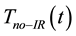 
were measured using Keithley 2000 multi-meters. The data were collected using LabView 2012 and a National Instruments PXI-1042q communications chassis.
During the measurements, the PG device and the power-meter sensor were positioned vertically and at an angle of incidence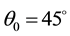 
with respect to the IR radiation. The instrumentation was placed in a closed sample compartment purged with N2 to prevent disturbances for the whole duration of the measurements versus time of 
, 
, 
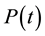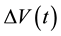and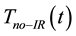 
[21]. The experimental parameters are summarized in Table 1.
3. Results and Discussion
a) Behavior in time of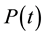 
In the 100 seconds immediately after starting the illumination of the power-meter sensor,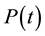 
, displayed in Figure 2(a), rises exponentially as follows:
![]()
Table 1.Summary of the experimental parameters in the main text and in the appendices.
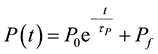, (5)
where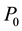 
is the offset, ![]()
the final value, and ![]()
the time constant. Typical values of these parameters are
reported in Table 2. The slope of the ![]()
graph in Figure 2(b) is negative, indicating the evolution
of ![]()
toward a stable fixed point [22] . The rate of increase of![]()
, i.e. the absolute value of the slope of
the ![]()
graph, is![]()
. The amplitude ![]()
of![]()
, i.e. the magnitude of the interval
along the horizontal scale of the ![]()
graph in Figure 2(b), is 21.5 mW. In the 50 hours after start-
ing the illumination of the power-meter sensor, the power![]()
, shown Figure 2(c), reaches a plateau. However, in multiple data sets, we always observe that ![]()
undergoes small sinusoidal instabilities shown in Figure 2(d) in which the vertical scale has been expanded. The instability, due to small periodic fluctuations in the closed sample compartment, can be fitted with:
![]()
, (6)
where ![]()
and ![]()
are the offset value and half of the separation between ![]()
and![]()
, respectively. The critical time ![]()
is the point in time in which ![]()
reaches![]()
, while ![]()
is the amount of time necessary to move ![]()
from ![]()
to ![]()
(practically, 1/4 of the period of the sinusoidal function). The typical values of![]()
, ![]()
, ![]()
, and ![]()
are reported in Table 2, labelled in Figure 2(d), and were obtained by placing the zero of the time-scale at the start of the illumination. The instability in ![]()
is small, as
inferred from![]()
. The ![]()
graph, shown in Figure 2(e), highlights a periodic behavior
with frequency![]()
! We observe the sinusoidal instability of![]()
, which modulates the amplitudes of the electric ![]()
and magnetic ![]()
fields of the IR radiation, to persist beyond the 50 h time interval in Figure 2(d).
We observed that the power ![]()
of the IR radiation rises exponentially obeying Equation (5) at the start of the illumination, and exhibits a sinusoidal instability in the 50 hours thereafter. For the entire time span, we hypothesize that the IR radiation transfers energy, through electric contribution![]()
, to the surface density
![]()
of the electrons on the illuminated Cu plate of the PG device, and contributes to producing ![]()
through the ![]()
and ![]()
fields (electric contribution) and ![]()
(entropic contribution).To prove that a link exists between ![]()
and![]()
, possibly also between ![]()
and![]()
, we sketch the behavior of![]()
and relate it to the observed![]()
, ![]()
, and![]()
.
To sketch![]()
, we hypothesize that, while hitting the surface of the Cu plate, the IR radiation modulates
the electric field ![]()
through the sinusoidal instability of the IR power![]()
. In
turn, ![]()
and its modulation act on the electrons of the Cu plate with force![]()
, where e is the electron’s charge. As in the photoelectric effect [3] , ![]()
displaces the electrons away from the location in which the IR radiation impinges on the Cu plate, locally decreasing their surface density such that![]()
. However, unlike in the photoelectric effect, ![]()
does not kick the electrons out of the Cu plate. In this process, ![]()
varies in time t as well as in space![]()
, i.e. the 2-dimensional (2D) surface of the Cu plate. To allow us versatility in choosing reference system, orientation and phase, we represent the 2D space variable ![]()
as the complex variable![]()
, where i is the imaginary unit. This choice resembles that adopted to describe light polariza-
tion through Jones matrices [23] -[25] . Thus,![]()
. All possible rotations of the refer-
ence system, phases, and positions in the 2D plane can be obtained by selecting magnitude and sign of![]()
, ![]()
, ![]()
, and![]()
.
With this choice of![]()
, upon starting the illumination, we picture ![]()
to exponentially decrease accord-
ing to![]()
, where ![]()
and ![]()
are the initial and final surface electron den-
sities, ![]()
the time constant, ![]()
a vector with units of inverse length, and ![]()
an arbitrary phase. We note that the exponential behavior is modulated by the oscillatory function![]()
.
In the subsequent 30 hours, from Equation (6) we expect ![]()
to undergo a slow variation in time such
that![]()
, where the sine function has the frequency ![]()
derived in Sec-
tion 3(a). With the choice of ![]()
discussed above, and utilizing the laws of trigonometric functions for complex variables, we obtain:
![]()
(7)
Here, ![]()
and ![]()
are the instability’s propagation velocities along the x and y directions; ![]()
and ![]()
are the lengths of the Cu plate along x and y; finally, ![]()
and ![]()
are the critical times of the surface electron density’s instability along x and y. Considering ![]()
and![]()
, the equilibrium electron density and its devia-
tion from equilibrium, respectively, we obtain![]()
. The 2D space variable
![]()
, therefore unveils a hyperbolic instability in ![]()
modulated by a sine function.
While ![]()
requires a spatiotemporal set of variables, the functions![]()
, ![]()
, ![]()
, and ![]()
are only time-dependent. To decouple ![]()
from the effects of ![]()
on![]()
, ![]()
, ![]()
, and![]()
, and allow time t to be the only effective variable, we integrate ![]()
over the surface area a of
the Cu plate as![]()
. Because of the capacitor-type structure of the PG device, with overall capacitance
C, we expect![]()
. This integration causes the loss of correlation between the phase of
![]()
and![]()
. In the 30 hours after starting the illumination, since ![]()
where![]()
, from Equation (7) we expect the ![]()
function to determine the behavior in time of![]()
. We also envision the capacitor-type structure of the PG device to affect ![]()
and![]()
, while leaving ![]()
constant.
Summarizing, we expect ![]()
to obey an exponential behavior in the first minutes after starting the illumination, and to exhibit a hyperbolic-secant-type of instability in the 30 hours thereafter, with no phase relationship with![]()
, no periodic behavior, and with ![]()
constant. We are currently exploring this hypothesis further numerically, which will be the focus of future work.
![]()
, (8)
![]()
Figure 3. Panels (a), (b), and (c) correspond to the away architecture and refer to the 400 seconds immediately following the start the illumination of the PG device with IR radiation. (a) Voltage difference ![]()
with fitting curves obeying Equation (8) highlighting the summands related to the electric (el) and the entropic (en) contributions; (b) Graph of ![]()
obtained from the fitting parameters in Table 3, reporting the slope and amplitude A; (c) Dimensionless voltage ![]()
as in Equation (9). Panels (d), (e), and (f) report the voltage difference![]()
, the ![]()
graph with slope and amplitude A, and the dimensionless voltage![]()
, respectively, for the toward architecture in the 400 seconds immediately following the start the illumination of the PG device with IR radiation. Panel (d) highlights the two summands related to the electric (el-1 and el-2) contributions, and the summand related to the entropic (en) contribution.
![]()
. (9)
![]()
, (10)
![]()
. (11)
In this expression, ![]()
and ![]()
are the offset and amplitude of the departure of ![]()
from the offset, respectively. The positive or negative sign of ![]()
corresponds to a downward or upward concavity, respectively, of the instability. The critical time ![]()
is the instant in which the maximum ![]()
value is achieved. Finally, the term H indicates the half width at half maximum (HWHM), or minimum (depending upon the sign of![]()
) of the instability. The magnitude of ![]()
corresponds to the long term equilibrium voltage
![]()
reported in Table 3. The typical values of![]()
, ![]()
, ![]()
, and H are reported in Table 4, labelled in Figure 6(a), and were obtained by placing the zero of the time-scale at the start of the illumination. We highlight that, since ![]()
in Figure 6(b) does not peak at![]()
, it does not correlate with the behavior in time of
![]()
. The instability in ![]()
is evidenced in the ![]()
graph in Figure 6(c), where stable
and unstable fixed points [20] alternate in a complex fashion without periodicity.
Since the time-dependence is enclosed in a hyperbolic secant function, we name the instability in ![]()
in Equation (11) and Figure 6(a) as hyperbolic instability. We establish the lack of correlation between![]()
, on one hand, and ![]()
and ![]()
on the other, as the criterion to identify such instability. Since the hyperbolic instability in ![]()
is absent in![]()
, as expected from Section 3(b), we relate the instability to the sole electric contribution.
Here we highlight the correlations existing between the power ![]()
and the voltage difference ![]()
to further support the choice of the fitting function in Equation (11) for ![]()
based on the hypothesis highlighted in Section 3(b).
We found that Equation (11), used to fit the hyperbolic instability in ![]()
in the 30 hours after starting the
illumination of the PG device with IR radiation, can be a solution of the equation:
![]()
. (12)
![]()
. (13)
![]()
. (14)
4. Summary and Significance
Acknowledgements
This work was supported by the U.S. Office of Naval Research (awards # N000141410378 N000141512158), JMU 4-VA Consortium (2013), Thomas F. Jeffress and Kate Miller Jeffress Memorial Trust (grant # J-1053), the Madison Trust―Fostering Innovation and Strategic Philanthropy-Innovation Grant 2015, the JMU Program of Grants for Faculty Assistance 2014, the JMU Center for Materials Science, and the JMU Department of Physics and Astronomy. The authors thank Dr. A. V. Zenkevich (Moscow Institute of Physics and Technology), Prof. G. Casati (University of Insubria, Italy), and Prof. D. J. Lawrence (JMU) for fruitful discussions.
Appendix-1
To highlight the effects of the entropic contribution and decouple it from the electric contribution, we collected the voltage difference ![]()
and the temperature difference ![]()
from the PG device activated by conductive heat transfer from a 100 W resistor in contact with the surface of the device. A temperature of ≈24˚C was generated by the PG device activated with a B&K Precision 1665 power supply providing 0.02 A and 3.2 V to the resistor. The achieved temperature is of the same order of magnitude as that detected when IR radiation hits the PG device, as can be seen in Figure 5(c) and Figure 5(d). We used a PG device 07111-9L31-04B by Custom Thermoelectric Inc. finished with an AlO plate (not with a Cu plate) and, in selected cases, gaffer tape. We placed the sample holders on both sides of the PG device in the toward architecture to create a capacitor structure with electrodes on both faces and thus avoid the “decay” in ![]()
shown in Figure 3(d). The experiments investigating the effects of conductive heat transfer were performed in an insulated sample compartment described in Ref. [30] . The PG device was horizontally fixed on the sample holders in all the measurements. When the IR radiation was used to compare the results obtained with conductive heat transfer, the PG device was also positioned horizontally and at an angle of incidence ![]()
with respect to the IR radiation. The basic experimental parameters are summarized in Table 1.
In the 400 seconds immediately following the start the activation of the PG device by either conductive heat transfer or IR radiation, we measured the rate of increase of ![]()
(![]()
) and ![]()
(![]()
), and the ratio ![]()
between the jumps in voltage ![]()
and temperature difference ![]()
in the away and toward architectures. We report the average values of![]()
, ![]()
, and R, alongside their uncertainties, in Figures A1(a)-(c), respectively. Figure A1(a) indicates that the average ![]()
values obtained by activating the PG device with IR radiation are always larger than those obtained by activating the PG device using conductive heat transfer. Figure A1(b) suggests that the average ![]()
values have a common value, independently of the source of activation of the PG device. Moreover, the average ![]()
and ![]()
values are similar when the PG device is activated by conductive heat transfer. In addition, the ![]()
values coincide with those derived from Figure 4(b) and Figure 4(d). This finding supports the identification of the contribution to energy transfer with slower rate of increase with the entropic contribution. Figure A1(c) shows that, within the errors, the average
value of the ratio R is larger when the PG device is activated by IR radiation through the electric contribution.
In the 400 seconds immediately following the start the activation of the PG device by either conductive heat transfer or IR radiation, we also measured the jump in voltage ![]()
obtained performing measurements on the PG device described above and finished with colored gaffer tape. We performed the measurements for the away and toward architectures. Figure A2(a) displays the magnitude of ![]()
obtained by activating the PG device with conductive heat transfer from a 100 W resistor. The observed trends are neither affected by the color nor by the presence of the tape. On the other hand, Figure A2(b) shows that the magnitude of ![]()
obtained by activating the PG device with IR radiation, is slightly sensitive to the color of the tape, and exhibits a noticeable drop when the tape is absent. Interestingly, the black-colored tape on the illuminated face of the PG device doubles the magnitude of ![]()
compared to the case without tape. Values of ![]()
above 0.5 mV, repre- sented by the horizontal line in Figure A2(b), can be achieved only with tape present on the illuminated face of the PG device. Thus, we conclude that the tape profoundly affects the capacitor-type behavior of the PG device.
In the time span of about 50 hours following the start of the activation of the PG device with conductive heat transfer from a 100 W resistor, the voltage difference![]()
, temperature difference![]()
, and temperatures![]()
and ![]()
of the activated and non-activated faces, respectively, are shown in Figures A3(a)-(d). We collected the particular set of data chosen using the PG device described above, finished with pink-colored gaffer tape, and set-up in the away architecture. Nevertheless, Figure A3 is representative of all the data collected in the away and toward architectures, with tape of all the available colors, and without tape. In all these cases, we observed![]()
, ![]()
, ![]()
, and ![]()
to be featureless and follow the same trends. The trend of![]()
is symmetric to that of![]()
, ![]()
, and![]()
. This behavior differs from that observed for the PG device activated by the IR radiation and captured in Figure 5. In this case, ![]()
and the temperatures ![]()
and ![]()
of the illuminated and non-illuminated faces are strongly correlated, while ![]()
is flat and featureless.
The results in Figures A1-A3, together with those of Figures 3-5, further support that the electric and the entropic contribution to energy transfer from low power IR radiation to the PG device are decoupled.
Appendix-2
Figure 6 shows the hyperbolic instability revealed in the voltage difference ![]()
in the time span of about 30 hours following the start of the illumination of the PG device with IR radiation in the away architecture. We identify such hyperbolic instability when no correlation is found between ![]()
and the temperatures ![]()
and ![]()
of the illuminated and non-illuminated faces of the PG device, respectively, and when ![]()
is flat. To demonstrate that hyperbolic instabilities are common in the interaction between IR radiation and a PG device, we collected a set of measurements with the PG device described in Appendix-1. With the AlO plate or
the layer of tape facing the IR radiation, the surface density ![]()
refers to the charges in the AlO plate or in the tape. The results, summarized in Figure A4, report the average values of the critical time (![]()
) and amplitudes (![]()
) of the revealed hyperbolic instabilities. We found a correlation neither between the values of ![]()
in Figure A4(a) and the signs of ![]()
in Figure A4(b), nor between these quantities and the away or toward architectures. However, by observing Figure A4(a), we found that ![]()
is typically located around![]()
, which is about twice the magnitude of ![]()
at ![]()
for the sinusoidal instability in ![]()
of the IR source reported in Table 2. In addition, we noted lower values for ![]()
in Figure A4(a) located around![]()
, i.e. in the neighborhood of![]()
. These observations highlight the correlations existing between the instabilities in ![]()
and ![]()
as already discussed in Section 3(e). Furthermore, in Figure A4(b) we noted randomness in the sign of![]()
, which we attribute to the loss of correlation between the phase of ![]()
and![]()
, and then between ![]()
and![]()
. We predicted the loss of phase relationship in Section 3(b).
We summarize the findings in Figure A4 as follows: the hyperbolic instability in ![]()
is a common
phenomenon, which is linked with the sinusoidal instability in the power ![]()
of the IR radiation.
NOTES
*Corresponding authors.