1. Introduction
Mystery of terrestrial magnetic field for several centuries attracts researchers. One of the first European scholars of modern formation W. Gilbert (see Figure 1) published in 1600 the book “On the Magnet, Magnetic Bodies and a Large Magnet―The Earth” [1] .
It is accepted to believe that the dipole character of the main Earth’s magnetic field with the value approximately equal to 1 Oe near the poles is the most important experimental fact that the model of Earth’s magnetism should explain. W. Gilbert suggested that inside the Earth there was a central region filled with magnetized ferromagnet (if to use the modern term). Later studies showed that the temperature in the central area of the Earth was so high―above the Curie temperature of ferromagnetic materials. Therefore, the magnetized core of the Earth cannot exist.
Later different models of the Earth’s magnetic field were offered. In particular, there were several models based on the effect of thermoelectricity. In the 40s of the last century a model dynamo was developed [2] . It obtained the recognition of experts.
The Blackett’s hypothesis:
Baron P. M. S. Blackett, Nobel Laureate and President of the Royal Society of London (Figure 2), offered another solution for the problem of the magnetic fields of celestial bodies [3] . He suggested that the magnetic field was generated not only a moving electric charge, but any moving neutral massive body too.
Later the assumption arose that this might be due to the fact that the electric charges of the electron and proton are not equal to each other. It is estimated that the difference between them may be very small―on the level of 10−18 e. However, such an insignificant difference was enough to explain the measured magnetic moments of all the celestial bodies.
Naturally, the relationship between the magnetic moment of the celestial body 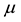 and its angular momentum L must exist with this approach.
and its angular momentum L must exist with this approach.
P. M. S. Blackett showed that the ratio of these values (the gyromagnetic ratio) must depend on the universal constants only:
 (1)
(1)
where G is gravity constant, and c is the light velocity.
![]()
Figure 1. William Gilbert (1544-1603)―English physicist, proposed the first model of terrestrial magnetism, introduced the concepts of electric and magnetic fields.
![]()
Figure 2. Nobel laureate baron Patrick Maynard Stuart Blackett (1897-1974).
However, the hypothesis Blackett was rejected, in spite of its beauty and attractiveness. Blackett abandoned it after thoroughly executed precise experiments. These experimenters have shown that electrically neutral massive bodies do not produce the magnetic field with required intensity.
1.1. The Measurement Data of Magnetic Fields of Celestial Bodies
Geophysics dealing with terrestrial magnetism problem, are thinking often that their main task is to construct a theory that would explain the reason why the main Earth’s magnetic field near the poles is approximately equal to 1 Oe. In the second half of the twentieth century, this formulation of the problem turned out to be unacceptable. After beginning of cosmic flying this geophysical problems turned into a special case of the more general problem of magnetism of cosmic bodies.
Flying of spacecrafts and general progress of astronomical techniques have discovered a wonderful, previously unknown fact: the magnetic moments of all the celestial bodies of the Solar system, as well as a number of stars and pulsars, are proportional to the torque of these cosmic bodies (Figure 3), as it should be in accordance with the Blackett’s hypothesis.
It is remarkable that this relationship keeps linearity in the range of about 20 orders of magnitude!
1.2. Atomic Matter and Plasma
All around us terrestrial matter has the atomic structure.
This means that the density of all materials in a condensed state (not in the gaseous state) is determined by the interaction between the electron shells of neighboring atoms.
The heat capacity of atomic matter is positive. Therefore, the thermal energy of the terrestrial bodies tends to the minimum (to zero) at .
.
The gravitational field with the acceleration  generates a force
generates a force 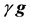 if atomic substance has density
if atomic substance has density .
.
In atomic matter, this force is balanced by the pressure gradient , which occurs in the interaction of atomic shells.
, which occurs in the interaction of atomic shells.
The equilibrium state for atomic matter in gravitational field is described by Euler’s equation:
![]()
Figure 3. The observed values of magnetic moments of celestial bodies vs. their angular momenta [4] . In ordinate, the logarithm of the magnetic moment (in Gs・cm3) is plotted; in abscissa the logarithm of the angular momentum (in erg・s) is shown. The line illustrates the Blackett’s ratio (1).
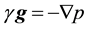 (2)
(2)
Another kind of matter (non atomic) is plasma. It was discovered in the middle of the last century.
All atomic materials transform in plasma state under action of high enough pressures or temperatures. At that atoms are ionized completely or partially. The result electron gas and naked nuclei or ions form electron-nuclear or electron-ion plasma.
The properties of plasma are radically different from properties of atomic matter. Together with the lack of electron shells, their interaction disappear. As a result the action of gravity can not create a gradient of pressure in plasma.
1.3. The Properties of a Hot Dense Plasma
As shown [5] , at the energetically favourable state, the hot dense plasma has finite density and finite temperature.
1.3.1. The Corrections to Boltzman’s Distribution for Hot Plasma
At very high temperatures, the electron gas of plasma obeys Boltzman’s statistics. But even at very high temperatures, it is possible in the first approximation only. For more accurate description its properties, the specificity of the plasma particle interaction must be taken into account and two main corrections to ideal gas law must be introduced.
The first correction takes into account the quantum character of electrons, which obey the Pauli principle, and cannot occupy levels of energetic distribution which are already occupied by other electrons. This correction must be positive because it leads to an increased gas incompressibility.
Other correction takes into account the correlation of the screening action of charged particles inside dense plasma. It is the so-called correlational correction. Inside a dense plasma, the charged particles screen the fields of other charged particles. It leads to a decreasing of the pressure of charged particles. Accordingly, the correction for the correlation of charged particles must be negative, because it increases the compressibility of electron gas.
1.3.2. The Correction for the Fermi-Statistic
As the full energy of a non-relativistic Fermi-particle system [6] :
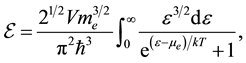 (3)
(3)
the energy of electron gas in the Boltzmann’s case 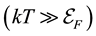 can be calculated at expanding it in a series. (Where
can be calculated at expanding it in a series. (Where 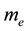 is electron mass,
is electron mass, 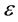 is the energy of electron and
is the energy of electron and ![]() is its chemical potential.)
is its chemical potential.)
In the Boltzmann’s case, ![]() and
and ![]() and the integrand at
and the integrand at ![]() can be expanded into a
can be expanded into a
series according to powers![]() . If we introduce the notation
. If we introduce the notation ![]() and conserve the two first terms of
and conserve the two first terms of
the series, we obtain
![]() (4)
(4)
or
![]() (5)
(5)
Thus, the full energy of the hot electron gas is
![]() (6)
(6)
Using the definition of a chemical potential of ideal gas (of particles with spin = 1/2) [6]
![]() (7)
(7)
we obtain the full energy of the hot electron gas
![]() (8)
(8)
where ![]() is the Bohr radius.
is the Bohr radius.
1.3.3. The Correction for Correlation of Charged Particles
Even at high temperatures in plasma, there is some correlation in space distribution of particles. It arises as particles with one electric charge surround themselves preferably by particles of other charge.
It is accepted to estimate the energy of this correlation by the method developed by Debye-Hükkel for strong electrolytes [6] . The energy of a charged particle inside plasma is equal to![]() , where e is the charge of a particle, and
, where e is the charge of a particle, and ![]() is the electric potential induced by other particles on the considered particle.
is the electric potential induced by other particles on the considered particle.
This potential inside plasma is determined by the Debye law [6] :
![]() (9)
(9)
where the Debye radius is
![]() (10)
(10)
For small values of ratio![]() , the potential can be expanded into a series
, the potential can be expanded into a series
![]() (11)
(11)
The following terms are converted into zero at![]() . The first term of this series is the potential of the considered particle. The second term
. The first term of this series is the potential of the considered particle. The second term
![]() (12)
(12)
is a potential induced by other particles of plasma on the charge under consideration. And so the correlation energy of plasma consisting of ![]() electrons and
electrons and ![]() nuclei with charge Z in volume V is [6]
nuclei with charge Z in volume V is [6]
![]() (13)
(13)
1.4. The Energy-Preferable State of a Hot Plasma
1.4.1. The Energy-Preferable Density of a Hot Plasma
Finally, at taking into account both main corrections, the full energy of plasma is given by
![]() (14)
(14)
The equilibrium state of plasma exists at the minimum of its full energy:
![]() (15)
(15)
This equilibrium condition corresponds to the equilibrium density of the electron gas of a hot plasma
![]() (16)
(16)
1.4.2. The Estimation of Temperature of Energy-Preferable State of a Hot Stellar Plasma
At known steady-state value of the density of hot plasma, we can obtain its energy-preferable temperature.
The virial theorem [6] [7] claims that the full energy of particles E, if they form a stable system with the Coulomb law interaction, must be equal to their kinetic energy T with a negative sign. Neglecting small corrections at a high temperature, one can write the full energy of a hot dense plasma as
![]() (17)
(17)
where ![]() is the potential energy of the system, G is the gravitational constant,
is the potential energy of the system, G is the gravitational constant, ![]() and
and ![]() are the mass and the radius of the star.
are the mass and the radius of the star.
As the plasma temperature is high enough, the energy of the black radiation cannot be neglected. The full energy of the stellar plasma depending on the particle energy and the black radiation energy
![]() (18)
(18)
at equilibrium state must be minimal, i.e.
![]() (19)
(19)
This condition at ![]() gives a possibility to estimate the temperature of the hot stellar plasma at the steady state:
gives a possibility to estimate the temperature of the hot stellar plasma at the steady state:
![]() (20)
(20)
The last obtained estimation can raise doubts. At “terrestrial” conditions, the energy of any substance reduces to a minimum at![]() . It is caused by a positivity of a heat capacity of all of substances. But the steady-state energy of star is negative and its absolute value increases with increasing of temperature (Equation (17)). It is the main property of a star as a thermodynamical object. This effect is a reflection of an influence of the gravitation on a stellar substance and is characterized by a negative effective heat capacity. The own heat capacity of a stellar substance (without gravitation) stays positive. With the increasing of the temperature, the role of the black radiation increases
. It is caused by a positivity of a heat capacity of all of substances. But the steady-state energy of star is negative and its absolute value increases with increasing of temperature (Equation (17)). It is the main property of a star as a thermodynamical object. This effect is a reflection of an influence of the gravitation on a stellar substance and is characterized by a negative effective heat capacity. The own heat capacity of a stellar substance (without gravitation) stays positive. With the increasing of the temperature, the role of the black radiation increases![]() . When its role dominates, the star obtains a positive heat capacity. The energy minimum corresponds to a point between these two branches.
. When its role dominates, the star obtains a positive heat capacity. The energy minimum corresponds to a point between these two branches.
2. The Internal Structure of Stars
As the hot dense plasma at the minimum energy has the constant temperature and density, the pressure gradient in it must be absent. This is possible if a gravity induced electric polarization ![]() arises in plasma:
arises in plasma:
![]() (21)
(21)
For greater clarity, this equation can be rewritten using the laws of electrodynamics, if we introduce the density of the effective bound charge:
![]() (22)
(22)
At that the effective field strength of this effective charge:
![]() (23)
(23)
With using of these effective parameters, the equilibrium equation for hot dense plasma can be rewritten as:
![]() (24)
(24)
It should be stressed that the effective value of ![]() and
and ![]() are introduced for clarity of the recording of a balance of forces. At that as a stellar core is electrically polarized and its electroneutrality is stored.
are introduced for clarity of the recording of a balance of forces. At that as a stellar core is electrically polarized and its electroneutrality is stored.
2.1. The Equilibrium of Plasma in the Stellar Core
The equilibrium condition (21) for plasma with energetically favourable density ![]() is reached at
is reached at
![]() (25)
(25)
where ![]() is mass density, A and Z are the mass and charge number of nuclei from which composed plasma,
is mass density, A and Z are the mass and charge number of nuclei from which composed plasma, ![]() is proton mass.
is proton mass.
At that plasma obtains an effective charge with density
![]() (26)
(26)
and effective electric field acting on plasma
![]() (27)
(27)
2.2. Basic Parameters of Stellar Core
As both equilibrium plasma density ![]() and equilibrium temperature
and equilibrium temperature ![]() are known, we can estimate the stellar core mass
are known, we can estimate the stellar core mass ![]() and its radius
and its radius![]() .
.
According to the virial theorem, the potential energy of particles executing a finite motion must be equal to twice their kinetic energy (with the opposite sign as the potential energy of the related particle is negative):
![]() (28)
(28)
where ![]() is full number of particles in the plasma core of star.
is full number of particles in the plasma core of star.
With using obtained definitions (16) and (20), we get radius of electrically polarized stellar core
![]() (29)
(29)
where ![]() is the Chandrasekhar’s mass.
is the Chandrasekhar’s mass.
At that the mass of stellar core
![]() (30)
(30)
Calculations of the total mass of star show that it exceeds the mass of the core twice [5] [8] :
![]() (31)
(31)
2.3. Magnetic Moments of Stars
A thin spherical surface with radius r carrying an electric charge q at the rotation around its axis with frequency ![]() obtains the magnetic moment
obtains the magnetic moment
![]() (32)
(32)
The rotation of a ball charged at density ![]() will induce the magnetic moment
will induce the magnetic moment
![]() (33)
(33)
Thus the positively charged core of a star induces the magnetic moment
![]() (34)
(34)
The negative charge equal to positive volume one is distributed on the surface of the stellar core.
A polarization of stellar matter located above the core―in the stellar atmosphere―we are not taken into account.
The negative surface charge creates a magnetic moment
![]() (35)
(35)
So the total magnetic moment of the core is
![]() (36)
(36)
Simultaneously, the torque of a ball with mass ![]() and radius
and radius ![]() is
is
![]() (37)
(37)
As a result, the giromagnetic ratio for celestial bodies where the force of their gravity induces the electric polarization will depend on world constants only:
![]() (38)
(38)
This relation was obtained for the first time by P. M. S. Blackett [3] . He shows that giromagnetic ratios of the Earth, the Sun and the star 78 Vir are really near to![]() .
.
By now the magnetic fields, masses, radii and velocities of rotation are known for all planets of the Solar system and for a some stars. These measuring data are shown in Figure 3, which is taken from [4] . It is possible to see that these data are in satisfactory agreement with Blackett’s ratio. At some assumption, the same parameters can be calculated for pulsars. All measured masses of pulsars are equal by the order of magnitude [10] . It is in satisfactory agreement with the condition of equilibrium of relativistic matter [9] . It gives a possibility to consider that masses and radii of pulsars are determined. According to generally accepted point of view, pulsar radiation is related with its rotation, and it gives their rotation velocity. These assumptions permit to calculate the giromagnetic ratios for three pulsars with known magnetic fields on their poles [11] . It is possible to see from Figure 3, the giromagnetic ratios of these pulsars are in agreement with Blackett’s ratio.
3. The Terrestrial Magnetic Field. Introduction
It should be noted that the construction of the theory of the terrestrial magnetic field is not possible without a more common approach.
With the beginning it is necessary to construct a theory of the internal structure of the Earth. Only after that we can build a model of the mechanism, the exciting magnetic field in the bowels of the Earth.
The ratio between the average density of the Earth ![]() and the density of matter near its surface and direct seismic measurements indicates that Earth has a high-density core. The modern model of the Earth assumed that it has a liquid conductive (metal) core.
and the density of matter near its surface and direct seismic measurements indicates that Earth has a high-density core. The modern model of the Earth assumed that it has a liquid conductive (metal) core.
This view on the state of the core goes back to G. Leibniz, who expressed it, watching the work of melting blast furnace in the XVII century. Into a blast furnace, a heavy molten metal fell down, and light slag floated.
It seems that the Earth’s core can be formed from heavy metals also by gravity.
This assumption is wrong.
This is certainly not the case. Near the center of a cosmic body, gravity is weak. In the center, it is simply equal to zero.
So high-density core of the Earth must be formed by the action of another mechanism.
Such a mechanism is the conversion of any solid material in plasma.
Under the influence of very high pressure, all atoms of stellar matter completely lose all the electron shells and intrastellar plasma consists of electrons and naked nuclei.
The pressures and temperatures that exist within the planet, less than stellar several orders of magnitude. Their impact is not enough to pull all the electrons from the atoms. They are torn from each atom only a few electrons from the outer shells. As a result, in the central core of the planet must form electron-ion plasma.
There is no simple method to determine how many atomic shells will be destroyed as a result of this action and what would be the volume of the plasma core. This can be achieved by method of minimization of the total energy of the planet [12] .
This is main task of next part of this article.
4. The Theory of Earth Constructed by Method of Minimization of Its Full Energy
4.1. About the Equation of State
First, to create a theory of the Earth, we need to find the radial dependence of the terrestrial matter density![]() . To do this, it is necessary to write the equation of equilibrium for forces applied to the matter and the state equation of matter, i.e. the dependence of the matter density on the pressure. It is assumed that at small pressures the dependence of the matter density
. To do this, it is necessary to write the equation of equilibrium for forces applied to the matter and the state equation of matter, i.e. the dependence of the matter density on the pressure. It is assumed that at small pressures the dependence of the matter density ![]() on the pressure p is described by Hook’s law:
on the pressure p is described by Hook’s law:
![]() (39)
(39)
i.e. at small pressures the equation of state is
![]() (40)
(40)
where ![]() is the matter density at zero pressure; B is the bulk module of matter. At high pressures the bulk module itself starts to depend on the density. This dependence can be described by the polytropic function
is the matter density at zero pressure; B is the bulk module of matter. At high pressures the bulk module itself starts to depend on the density. This dependence can be described by the polytropic function
![]() (41)
(41)
where ![]() is a constant, k is a polytropic index describing the elastic property of matter (
is a constant, k is a polytropic index describing the elastic property of matter (![]() describes incompressible matter). Thus, the equation of state can be written as
describes incompressible matter). Thus, the equation of state can be written as
![]() (42)
(42)
At small pressures it transforms into Hook’s law and at higher pressures it transforms into the standard polytropic equation
![]() (43)
(43)
4.2. The Core and the Mantle
Let us assume that the considered spherical body (the Earth or any other planet) is divided into two regions―an inner core and an outer mantle. Thus, we shall assume that the mantle is composed of hard rock of the basalt type and is characterized, as generally accepted, by a polytropic index![]() .
.
Under action of ultrahigh pressure, atoms in the core lose their outer electron shell to reduce their volume and form dense plasma. In this state, substance is characterized by the polytropic index![]() . Plasma is electrically polarized matter and we can assume that the matter inside the core may be electrically polarized by gravity if it is energetically favorable.
. Plasma is electrically polarized matter and we can assume that the matter inside the core may be electrically polarized by gravity if it is energetically favorable.
As a rule, this possibility is not considered at all on the basis of the fact that the electrical polarization is connected with the appearance of some additional energy and is, therefore, energetically disadvantageous. At the same time, it escapes completely everybody’s attention, that the electrical polarization changes and even can reduce other types of energy, such as gravitational and inner energy. Assuming that the core of the planet can be electrically polarized, we shall have as a purpose of our solution the determination of its radius ![]() for the minimum of its full energy. If this configuration corresponds to the body with zero
for the minimum of its full energy. If this configuration corresponds to the body with zero![]() , it will mean that the separation of the planet into an electrically polarized core and an unpolarized mantle is energetically disadvantageous. In view of mechanical strains, we shall assume that the planet matter has a homogeneous chemical composition with the density
, it will mean that the separation of the planet into an electrically polarized core and an unpolarized mantle is energetically disadvantageous. In view of mechanical strains, we shall assume that the planet matter has a homogeneous chemical composition with the density ![]() and the bulk module
and the bulk module ![]() at zero pressure. We shall assume that the electrical polarization intensity
at zero pressure. We shall assume that the electrical polarization intensity ![]() inside a core is proportional to gravity
inside a core is proportional to gravity
![]() (44)
(44)
Thus, inside the core the effect of gravitation is completely compensated by the electric force
![]() (45)
(45)
where ![]() is the density of matter inside the core, g is the gravity acceleration,
is the density of matter inside the core, g is the gravity acceleration, ![]() is the charge density connected with polarization,
is the charge density connected with polarization, ![]() is the electric field strength connected with polarization. This becomes possible because the behavior of gravitational and electric field intensities has similar descriptions:
is the electric field strength connected with polarization. This becomes possible because the behavior of gravitational and electric field intensities has similar descriptions:
![]() (46)
(46)
Due to such an electrical polarization distribution a bounded volume electric charge exists inside the core and on its surface there is a surface charge of the opposite sign so that the total electric charge of the core is equal to zero. It is easy to see that the polarization jump on the core surface is immediately accompanied with a pressure jump or, speaking in terms of bounded charges, the surface charge tends to compress the charged core. Thus, although the effect of gravity in the core is compensated, its matter experiences the pressure of the entire mass over its surface
![]() (47)
(47)
(![]() indicates that its value is taken on the core surface) and the pressure of the surface charge [13] [14] :
indicates that its value is taken on the core surface) and the pressure of the surface charge [13] [14] :
![]() (48)
(48)
This additional compression has a significant value, which is assumed to be sufficient to transform the core matter into the plasma state. In this case, the polarization sign is evident as soon as in this process the core matter acquires a positive charge while electrons are pushed out to the core surface. Estimations show that since the force of gravitation is weak compared to the electric force, the charge related to each ion is only about ![]() of the electron charge (for the case of terrestrial gravitation).
of the electron charge (for the case of terrestrial gravitation).
Since the compressibility of dense plasma is determined by the bulk module of Fermi gas, the polytropic index of such a matter is 3/2. In this case, the pressures inside the core and the core density are constant,
![]() (49)
(49)
As a result, the density inside the core is higher than the one that would exist inside the planet in the absence of polarization. The equilibrium state of the mantle matter is described by
![]() (50)
(50)
where ![]() is the mass of the matter confined to the radius r:
is the mass of the matter confined to the radius r:
![]() (51)
(51)
Thus, from Equation (50) for the mantle matter, we have
![]() (52)
(52)
where ![]() and
and ![]() is the radius of the planet in the case when it is composed of incompressible matter. Under strain the full mass of the planet is naturally conserved
is the radius of the planet in the case when it is composed of incompressible matter. Under strain the full mass of the planet is naturally conserved
![]() (53)
(53)
Solving together Equations (49), (52), and (53), we find ![]() and the ratio
and the ratio ![]() as functions of
as functions of![]() .
.
4.3. The Energy of a Planet
Next, we have to answer the principal question of whether the existence of an electrically polarized core is energetically advantageous. The gravitational energy of the spherical body under the definition is
![]() (54)
(54)
It can be found for the known density distribution inside a planet![]() . Furthermore, accounting to the thermodynamic equation for chemical potential
. Furthermore, accounting to the thermodynamic equation for chemical potential
![]() (55)
(55)
(where ![]() is the ion mass) from the equation of state Equation (42), the chemical potential is
is the ion mass) from the equation of state Equation (42), the chemical potential is
![]() (56)
(56)
and the density of the internal energy of the core is
![]() (57)
(57)
Doing analogous calculations for the mantle, we obtain
![]() (58)
(58)
The electric energy exists only inside the core and its density is
![]() (59)
(59)
Since the thermal energy is neglected, to calculate the full energy of the planet, it is necessary to integrate Equations (57), (58), and (60) over the volume of the planet and sum them and Equation (54). To do this, we need to determine the values of constants composing these equations.
4.4. The Density Distribution inside the Earth
The mass M and radius R of the Earth are known. Therefore, we know the average density of the Earth![]() . On the basis of the geophysical data, we accept that the density of matter and bulk module on the surface of the mantle is
. On the basis of the geophysical data, we accept that the density of matter and bulk module on the surface of the mantle is ![]() and
and![]() . These values are characteristic for basalts [16] . Based on the above said we determine
. These values are characteristic for basalts [16] . Based on the above said we determine ![]() and the parameter
and the parameter![]() . We can found the value of the parameter
. We can found the value of the parameter ![]() as we know the values of
as we know the values of ![]() and
and ![]() and therefore we can find the ratio
and therefore we can find the ratio
![]() (60)
(60)
Next from all possible solutions we choose the one that actually meets the condition (60). In fact this procedure is reduced to choosing the parameter![]() , i.e. the ion mass related to each free electron in electron-ion plasma of the core. The total energy (related to
, i.e. the ion mass related to each free electron in electron-ion plasma of the core. The total energy (related to![]() ) is plotted as a function of the parameter
) is plotted as a function of the parameter ![]() in Figure 4. The dependence of the outer radius of the planet R (related to
in Figure 4. The dependence of the outer radius of the planet R (related to![]() ) over the core radius
) over the core radius ![]() at different values of
at different values of ![]() is shown in Figure 5. It can be seen that of the whole family only the curve obtained on the condition that in the core there exist approximately 22 nucleons per electron of electron-ion plasma satisfies
is shown in Figure 5. It can be seen that of the whole family only the curve obtained on the condition that in the core there exist approximately 22 nucleons per electron of electron-ion plasma satisfies
to the ratio ![]() (Equation (60)) for
(Equation (60)) for![]() .
.
Finally, knowing ![]() and
and![]() , we can find the distribution of the density of matter inside the planet. This is illustrated in Figure 5 for
, we can find the distribution of the density of matter inside the planet. This is illustrated in Figure 5 for ![]() (
(![]() is the proton mass) and
is the proton mass) and![]() .
.
Thus, the calculation shows that for the Earth it is energy advantageous to have an electrically polarized core. Radius ![]() and density
and density ![]() of the core are approximately equal to
of the core are approximately equal to ![]() and 10 g/cm3, respectively. On the mantle-core interface, the matter density drops sharply to 5 g/cm3 and then it decreases almost linearly as the radius increases. The measured dependence of the matter density inside the Earth is shown also in Figure 6. It is determined by measuring the propagation velocity of seismic waves. Being different, the calculated and measured dependencies coincide in the principal feature, i.e. they both indicate the existence of approximately equal jumps of the density on the core-mantle interface at about the half-radius of the planet.
and 10 g/cm3, respectively. On the mantle-core interface, the matter density drops sharply to 5 g/cm3 and then it decreases almost linearly as the radius increases. The measured dependence of the matter density inside the Earth is shown also in Figure 6. It is determined by measuring the propagation velocity of seismic waves. Being different, the calculated and measured dependencies coincide in the principal feature, i.e. they both indicate the existence of approximately equal jumps of the density on the core-mantle interface at about the half-radius of the planet.
![]()
Figure 4. The dependence of the total energy of the planet (over![]() ) on the size of the polarized core composed of some metal with different averaged ion mass
) on the size of the polarized core composed of some metal with different averaged ion mass ![]() per one conductivity electron.
per one conductivity electron.
![]()
Figure 5. (a) The external radius of the planet R (over![]() ) vs. the size of the core
) vs. the size of the core![]() . (b) The same dependence to larger scale.
. (b) The same dependence to larger scale.
4.5. The Moment of Inertia and the Magnetic Moment of the Earth
Knowing the matter distribution between the core and the mantle and their sizes, it is possible to calculate the moment of inertia for our theory. For a spherical body with a radial density distribution, we have
![]() (61)
(61)
In our case, we obtain
![]() (62)
(62)
It is in good agreement with the measured value 0.331.
It is obvious that the most bright and important result of the developed theory is the understanding of the mechanism of the generation of the terrestrial magnetic field. It is very simple: the rotation of the electrically polarized core (together with the planet) about its axis with the frequency ![]() produces the magnetic moment
produces the magnetic moment
![]() (63)
(63)
Substituting appropriate values, we obtain ![]() which is almost exactly equal to one-half of the observed value of the moment
which is almost exactly equal to one-half of the observed value of the moment![]() .
.
5. Conclusion
For a sufficiently large planet the calculated radius of the core and the external radius have the same order of magnitude and the gyromagnetic ratio is approximately equal to
![]() (64)
(64)
(L is the angular momentum of the planet as a whole) or
![]() (65)
(65)
This allows us to explain the observed dependence of magnetic moments of space bodies by the existence of electrically polarized cores in them. Let us emphasize that the main difference from early models [16] [17] is that the developed one is an intrinsic self-consistent theory. In the earlier models it was assumed that the pressure inside a planet has a monotonous behavior. The density jump on the surface of the core was usually explained by the gravitational differentiation of the chemical composition since it was thought that the core was composed of metallic iron and the mantle was formed of the corresponding amount of rock. In the developed theory, the planet is composed of basalt-like matter with a homogeneous chemical. The jump of the pressure on the core surface is induced by electrical polarization. It leads to a density jump, which in turn makes energetically favorable the polarization of the core. It should be noted that it is possible to apply the developed theory for any space body with a sufficiently large mass. Actually, as is shown in [13] -[15] , the condition for the appearance of electrical polarization inside the planet can be reduced to the requirement that it has a sufficiently large mass. If a space body has the density and the bulk module characteristic for the Earth, its mass must be larger than 1026 g. Thus, the existence of polarization is energetically disadvantageous in small bodies such as Moon and asteroids. It is also necessary to mention that the developed theory does not substitute the dynamo- model. It simply completes it with the mechanism of the creation of a bare field. This statement is supported by the fact that the calculated magnetic moment of the Earth is two times smaller than its measured magnetic moment and that the magnetic moments of a number of other planets have the same order of magnitude as Equation (64) but the opposite sign. In conclusion, it is noted that the developed model is actually the theory of the Earth as it has no free parameters. In order to find the basic characteristics of the interior structure of the Earth, we use the numerical values of its mass and radius known unambiguously and the values of the density of matter and the bulk module on the mantle surface, whose were also not chosen arbitrarily.