1. Introduction
The general setting is as follows: Suppose we decompose a group G into direct product of subsets 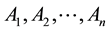 of G in such a way that each element g in G has a unique representation of the form
of G in such a way that each element g in G has a unique representation of the form 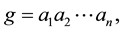 where
where . The question then asked is what we can say about the subsets
. The question then asked is what we can say about the subsets .
.
The answer is rather difficult even if we do not impose many restrictions either on G or on the subsets. The most important special case has some connection with a group-theoretial formulation by G. Hajós [1] of a conjecture by H. Minkowski [2] ; this is when G is a finite Abelian group and each of the subsets is of the form
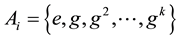 ,
,
where 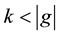 is an integer; here e denotes the identity element of g and
is an integer; here e denotes the identity element of g and 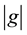 denotes order of the element g of G. Then a result due to Hajos states that one of the subsets
denotes order of the element g of G. Then a result due to Hajos states that one of the subsets 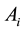 must be a subgroup of G. L. Rédei [3] generalizes this result to the case when the condition on the subsets
must be a subgroup of G. L. Rédei [3] generalizes this result to the case when the condition on the subsets  is that they contain a prime number of elements.
is that they contain a prime number of elements.
Another interesting question has also been asked by Hajos. It is concerned with the case in which G is an Abelian group and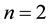 ; the question then asked is as follows: Suppose G has a decomposition as
; the question then asked is as follows: Suppose G has a decomposition as . Does it follow that one of the subsets
. Does it follow that one of the subsets 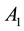 or
or 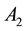 is a direct product of another subset and a proper subgroup of G?
is a direct product of another subset and a proper subgroup of G?
The concept of Hajós factorization begin group-theoretical but now finds applications in diverse fields such as number theory, [4] coding theory [5] and even in music [6] .
2. Preliminaries
Throughout this paper, G will denote a finite Abelian group, e the identity of G, and if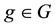 , then
, then 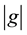 will denote its order. We will also use
will denote its order. We will also use ![]() to denote the number of elements of a subset A of G. A subset A of G of the form
to denote the number of elements of a subset A of G. A subset A of G of the form ![]() is called a cyclic subset of G; here k is an integer with
is called a cyclic subset of G; here k is an integer with![]() . If
. If
![]()
we say that we have a factorization of G. If in addition, each of the subsets ![]() contains e, we say that we have a normalized factorization of G. A subset A of G is called periodic if there exists
contains e, we say that we have a normalized factorization of G. A subset A of G is called periodic if there exists![]() , such that
, such that![]() . Such an element
. Such an element ![]() if it exists is called a period for A. A group G is said to be of type
if it exists is called a period for A. A group G is said to be of type![]() , if it is a direct product of cyclic groups of orders
, if it is a direct product of cyclic groups of orders![]() , (where of course
, (where of course ![]() are primes and
are primes and ![]() are non-negative integers).
are non-negative integers).
3. Remarks
1) If ![]() is a factorization of G , then for any
is a factorization of G , then for any![]() ,
, ![]() is also a factorization of G. Similarly, with
is also a factorization of G. Similarly, with![]() . Thus, we may assume that all factorization we consider are normalized.
. Thus, we may assume that all factorization we consider are normalized.
2) In the literature, a group G is said to be "good" if from each factorization![]() , it follows that one the subsets A or B is periodic.
, it follows that one the subsets A or B is periodic.
We extend the above definition as follows.
4. Definition
A group G has the Hajos-n-property or n-good if from any factorization
![]()
it follows that one of the subsets ![]() is periodic. Otherwise it is n-bad. We will also say G is totally- good if it is n-good for all possible values of n.
is periodic. Otherwise it is n-bad. We will also say G is totally- good if it is n-good for all possible values of n.
The following results are known and will be used in this paper.
Lemma 1 [7]
If G is of type![]() , then G is 2-good.
, then G is 2-good.
Lemma 2 [8]
A cyclic group G of order![]() , where
, where ![]() is prime is totally-good.
is prime is totally-good.
Lemma 3 [8]
If G is of type![]() , where
, where ![]() and
and ![]() is prime, then G is n-bad for all n,
is prime, then G is n-bad for all n,![]() .
.
Lemma 4 [9]
If H is a proper subgroup of G, then there exists a non-periodic set N such that ![]() is a factorization of G, except when H is a subgroup of index 2 in an elementary abelian 2-group.
is a factorization of G, except when H is a subgroup of index 2 in an elementary abelian 2-group.
Lemma 5 [7]
If A and B are non-periodic subsets o a group G and A is contained in a subgroup H of G such that ![]() is a factorization of G, then AB is also non-periodic.
is a factorization of G, then AB is also non-periodic.
5. Results
Theorem 6
If G is of type ![]() , then G is totally-good.
, then G is totally-good.
Proof.
Let ![]() be a factorization of G.
be a factorization of G.
Now, the possible values for n are 1, 2, 3 and 4.
The case ![]() is trivial.
is trivial.
The case ![]() follows from Lemma 1.
follows from Lemma 1.
The case ![]() follows from Rédei’s theorem.
follows from Rédei’s theorem.
So, we only need details the case![]() . So now,
. So now,![]() .
.
We may assume![]() . Now,
. Now, ![]() is also a factorization of G. Hence by Lemma 1, either
is also a factorization of G. Hence by Lemma 1, either ![]() is or
is or ![]() is periodic. If
is periodic. If ![]() is periodic, we are done. So assume
is periodic, we are done. So assume ![]() is periodic, say with period
is periodic, say with period![]() . We may assume
. We may assume![]() .
.
Let ![]() and
and![]() . Then
. Then![]() . If
. If![]() , then
, then ![]() is a subgroup and hence periodic, while if
is a subgroup and hence periodic, while if![]() , then
, then ![]() is a subgroup and hence periodic. Suppose
is a subgroup and hence periodic. Suppose![]() , then we must have either 1)
, then we must have either 1) ![]() and
and ![]() both of which give
both of which give![]() , which is impossible; or 2)
, which is impossible; or 2) ![]() and
and ![]() both of which imply that both
both of which imply that both ![]() and
and ![]() are subgroups of G. This ends the proof. ,
are subgroups of G. This ends the proof. ,
Theorem 7
If G is of type![]() , then G is 3-bad.
, then G is 3-bad.
Proof.
Let![]() , where
, where ![]() and
and![]() .
.
Let![]() ,
, ![]() and
and![]() .
.
Then ![]() is a factorization of G and none of the subsets
is a factorization of G and none of the subsets![]() ,
, ![]() or
or ![]() is periodic. This ends the proof. ,
is periodic. This ends the proof. ,
Theorem 8
Let H be a proper subgroup of a group G. If H is n-bad, then G is both n and ![]() -bad.
-bad.
Proof.
Since H is n-bad, there is a factorization ![]() of H, where none of the subsets
of H, where none of the subsets ![]() is periodic. Now, by Lemma 5, there is a factorization
is periodic. Now, by Lemma 5, there is a factorization ![]() of G, with
of G, with ![]() nonperiodic. Hence,
nonperiodic. Hence,
![]()
is a factorization G with none none of the subsets ![]() periodic. Thus, G is
periodic. Thus, G is ![]() -bad.
-bad.
Also, ![]() is a factorization G with none of the subsets periodic. Here, the non- periodicity of the factor
is a factorization G with none of the subsets periodic. Here, the non- periodicity of the factor ![]() follows from Lemma 5. This ends the proof. ,
follows from Lemma 5. This ends the proof. ,
Theorem 9
If G is of type![]() , where
, where![]() ,
, ![]() , then G is both 3 and 4-bad.
, then G is both 3 and 4-bad.
Proof.
G has a subgroup H of type ![]() which is 3-bad by Theorem 7.
which is 3-bad by Theorem 7.
So, the result follows from Theorem 8. This ends the proof.
Finally, we show by example what we aimed to show.
6. Example 1
Let ![]() be of type
be of type![]() . Then by Lemma 1,
. Then by Lemma 1, ![]() is 2-good. Now, consider the group
is 2-good. Now, consider the group ![]() and note that G is of type
and note that G is of type ![]() Observe that G has a subgroup H of type
Observe that G has a subgroup H of type ![]() which is 3-bad by Theorem 9. Now, by Lemma 4, G has a factorization
which is 3-bad by Theorem 9. Now, by Lemma 4, G has a factorization![]() , where N is nonperiodic. Hence, G has a factorization
, where N is nonperiodic. Hence, G has a factorization![]() , where none of the factor is periodic. Thus G is 4-bad. This ends the proof. ,
, where none of the factor is periodic. Thus G is 4-bad. This ends the proof. ,
7. Example 2
Let ![]() be of type
be of type ![]() and
and ![]() be of type
be of type![]() , where
, where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is prime. Then by Lemma 2,
is prime. Then by Lemma 2, ![]() is m-good for all m,
is m-good for all m, ![]() , and
, and ![]() is n-good for all m,
is n-good for all m,![]() . Consider the group
. Consider the group![]() . Then by Lemma 3,
. Then by Lemma 3, ![]() is
is ![]() -bad for all
-bad for all![]() ,
,![]() . This ends the proof. ,
. This ends the proof. ,