1. Introduction
At the beginning, we introduce the definition of exponential spline function. From literature [3] , we could learn
the definition: if function 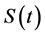 satisfies equation
satisfies equation , we describe it as exponential
, we describe it as exponential
spline function, where L is a differential operator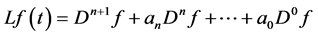 . Here,
. Here, 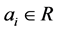
 are constant coefficient and
are constant coefficient and 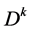 represent kth-order derivative. By this definition, we learn that
represent kth-order derivative. By this definition, we learn that 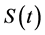 exists continuous derivative
exists continuous derivative 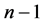 and in each interval
and in each interval  is linear combination of
is linear combination of
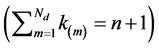
 , where the
, where the ’s are the Nd distinct roots of characteristic poly-
’s are the Nd distinct roots of characteristic poly-
nomial and 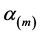 is of order
is of order . As exists a single root 0 for characteristic polynomial,
. As exists a single root 0 for characteristic polynomial, 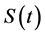 is polynomial spline function. Next we will deal with the case of there being unique real root.
is polynomial spline function. Next we will deal with the case of there being unique real root.
2. Main Result
Theorem 1:
If the differential operator’s characteristic polynomial is ![]()
![]() , where
, where ![]() is a root of multiplicity
is a root of multiplicity![]() . Then the expression for exponential spline function of this special case is
. Then the expression for exponential spline function of this special case is
![]()
Proof:
Let ![]() be on interval
be on interval![]() ,
, ![]() Suppose
Suppose
![]() And we have
And we have ![]()
![]()
Since there exists order ![]() continuous derivatives for
continuous derivatives for![]() ,
,
Hence
![]()
So that ![]()
Furthermore, ![]() is polynomial of nth degrees.
is polynomial of nth degrees.
Therefore ![]()
We get![]() ,
,
put ![]()
In terms of this idea, we obtain![]() .
.
Theorem 2: The dimension of the exponential spline function space is![]() .
.
Proof:
Suppose![]() ,
, ![]()
We have ![]()
Since ![]()
So that ![]() is continuous at the knot
is continuous at the knot![]() , hence
, hence ![]() has order
has order ![]() continuous derivatives on interval
continuous derivatives on interval![]() .
.
When characteristic polynomial has single real root, the linear space can be written as
![]()
Next we prove that ![]() is linearly independent
is linearly independent
Set ![]() On the interval
On the interval![]() , above equation become
, above equation become![]() , we
, we
have ![]() On the interval
On the interval![]() , we can get
, we can get![]() , so that
, so that![]() , For the interval
, For the interval![]() , By means of the same technique, we can obtain
, By means of the same technique, we can obtain![]() , hence
, hence ![]() is linearly independent. So that we conclude
is linearly independent. So that we conclude![]() .
.
According to theorem 1. 4. 23 of the book [4] , we can prove next conclusion is true.
Corollary: There exists the ![]() for every f belonging to
for every f belonging to![]() , such that
, such that
![]()
Theorem 3: If condition of interpolation and boundary satisfy:
![]() (1)
(1)
then there exist the 3rd degree exponential spline function satisfied with condition. And we have formula of error evaluation
![]()
Proof:
Suppose ![]() is 3rd degree polynomial spline function, let
is 3rd degree polynomial spline function, let ![]()
Hence ![]()
Both of them can be denoted by:![]() ,
, ![]() ,
, ![]() , so that A is invertible matrix.
, so that A is invertible matrix. ![]()
This lead to ![]() (2)
(2)
Since![]() , hence
, hence![]() , we can get
, we can get ![]() is exponential spline function.
is exponential spline function.
If boundary condition is![]() ,
, ![]() , by matrix relation (2), let
, by matrix relation (2), let
![]() and
and ![]()
Since one of 3rd degree polynomial spline function meet the constraint of interpolation![]() , boundary condition is
, boundary condition is ![]() and
and![]() .
.
So that exponential spline function satisfied with condition (1) exists. That is![]() .
.
Next we prove formula of error evaluation. Suppose![]() ,
, ![]() is 3rd degree exponential spline function satisfied with condition (1).
is 3rd degree exponential spline function satisfied with condition (1).
Let ![]() (where
(where ![]() is 3rd degree polynomial spline function)
is 3rd degree polynomial spline function)
![]()
Since ![]()
![]()
![]()
By formula of error evaluation for 3rd degree polynomial spline function, we can have
![]()
![]()
In terms of book [5] , we have
![]()
Since ![]()
Hence ![]()
Furthermore ![]()
By above expressions, we can conclude that
![]() .
.
Fund
Supported partly by National Natural Science Foundation of China (11126140, 11201007) and partly by Beijing Talents Training Program (2011D005002000006) and partly by Science and Technology Development Plan Project of Beijing Education Commission (KM20121000-9013) and partly by Scientific Research Personnel Promotion Plan of North China University of Technology (BJRC201309).