1. Introduction
When dealing with supervised learning, one of the main problems in classification activities lies in the treatment of datasets where one or more classes have a minority quantity of instances. This condition denotes an imbalanced dataset, which makes the algorithm to incorrectly classify one instance from the minority class as belonging to the majority class, and in highly skewed datasets, this is also denoted as a “needle in the haystack” problem [1] , due to the high number of instances from a class overcoming one or more minority classes. Nevertheless, in most of cases the minority class represents an abnormal event in a dataset, and usually this is the most interesting and valuable information to be discovered.
Learning from imbalanced datasets is still considered an open problem in data mining and knowledge discovery, and needs real attention from the scientific community [2] . The experiments performed in [3] demonstrated the class overlapping is commonly associated with the class imbalance problem. An empirical study was performed by [1] , in order to identify causes of why classifiers perform worse in the presence of class imbalance. In [4] the authors conducted a taxonomy of methods applied to correct or mitigate this problem, and in this study three main approaches were found: data adjusting, cost sensitive learning, and algorithm adjusting. In the data adjusting, there are two main sub-approaches: creation of instances from minority class (oversampling), and removal of instances from majority class.
This work is focused in the data adjusting algorithms, and a proposal of a KNN undersampling (KNN-Und) algorithm will be presented. The KNN-Und is a very simple algorithm, and basically it uses the neighbor count to remove instances from majority class. Despite its simplicity, the classification experiments performed with KNN-Und balancing resulted in better performance of G-Mean [5] and AUC [6] , in most of the 33 datasets, if compared with three methods based on KNN: SMOTE [7] , ENN [8] , NCL [9] , and the random undersampling method. The KNN-Und balancing also performed better than the results published previously by [10] in 11 of 15 datasets, and had higher average values of G-Mean and AUC, than the evolutionary algorithm proposed by [11] . The results obtained in the experiments show that KNN-Und and other balancing methods based on KNN are an interesting approach to solve the imbalanced dataset problem. Instead of generating new synthetic data as oversampling methods, especially when the datasets are approaching petabytes of size [12] , the oriented removal of majority instances can be a better solution than to create more data.
This paper is organized as follows. In Session 2 a literature review about KNN balancing methods is presented, in Session 3 the KNN-Und methodology is explained in more details. In section 4 the experiments conducted in this work will be presented, compared and commented, followed by the conclusions.
Imbalanced Dataset Definition
This section establishes some notations that will be used in this work.
Given the training set T with m examples and n attributes, where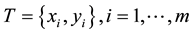 , and where
, and where  is an instance in the set of attributes
is an instance in the set of attributes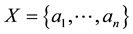 , and
, and 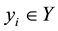 is an instance in the set of classes
is an instance in the set of classes , there is a subset with positive instances
, there is a subset with positive instances , and a subset of negative instances
, and a subset of negative instances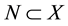 , where
, where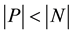 . All
. All
subset of P created by sampling methods will be denominated S. The pre-processing strategies applied to datasets aims to balance the training set T, such as .
.
2. Literature Review
Along the years, a great effort was done in the scientific community in order to solve or mitigate the imbalanced dataset problem. Specifically for KNN, there are several balancing methods based on this algorithm. This section will provide a bibliographic review about the KNN and its derivate algorithms for dataset balancing. Also, the random oversampling and undersampling methods, the class overlapping problem, and evaluation measures will be reviewed.
2.1. KNN Classifier
The k Nearest Neighbor (KNN) is a supervised classifier algorithm, and despite his simplicity, it is considered one of the top 10 data mining algorithms [13] . It creates a decision surface that adapts to the shape of the data distribution, enabling them to obtain good accuracy rates when the training set is large or representative. The KNN was introduced initially by [14] , and it was developed with the need of perform discriminant analysis when reliable parametric estimates of probability densities are unknown or difficult to determine.
The KNN is a nonparametric lazy learning algorithm. It is nonparametric because it does not make any assumptions on the underlying data distribution. Most of the practical data in the real world does not obey the typical theoretical assumptions made (for example, Gaussian mixtures, linear separability, etc....). Nonparametric algorithms like KNN are more suitable on these cases [15] [16] .
It is also considered a lazy algorithm. A lazy algorithm works with a nonexistent or minimal training phase but a costly testing phase. For KNN this means the training phase is fast, but all the training data is needed during the testing phase, or at the least, a subset with the most representative data must be present. This contrasts with other techniques like SVM, where you can discard all nonsupport vectors.
The classification algorithm is performed according to the following steps:
1. Calculate the distance (usually Euclidean) between a xi instance and all instances of the training set T;
2. Select the k nearest neighbors;
3. The xi instance is classified (labeled) with the most frequent class among the k nearest neighbors. It is also possible to use the neighbors' distance to weight the classification decision.
The value of k is training-data dependent. A small value of k means that noise will have a higher influence on the result. A large value makes it computationally expensive and defeats the basic philosophy behind KNN: points that are close might have similar densities or classes. Typically in the literature are found odd values for k, normally with k = 5 or k = 7, and [15] reports k = 3 allowing to obtain a performance very close to the Bayesian classifier in large datasets. An approach to determine k as a function (1) of data size m is proposed in [16] .
 (1)
(1)
The algorithm may use other distance metrics than Euclidean [17] [18] .
2.2. SMOTE
The SMOTE algorithm proposed by [7] is one of the most known oversampling techniques, being successful in several areas of application, being also a base for other oversampling algorithms [9] [19] - [22] .
The SMOTE executes the balancing of a P set of minority instances, creating n synthetic instances from each instance 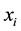 of the P set. The synthetic instance is created based in a minority instance and its nearest neighbors. One synthetic instance is generated based in the instances
of the P set. The synthetic instance is created based in a minority instance and its nearest neighbors. One synthetic instance is generated based in the instances 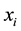 and
and , being
, being 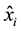 an instance randomly selected among the k nearest neighbors (KNN) of
an instance randomly selected among the k nearest neighbors (KNN) of , and
, and ![]() as a random number between 0 and 1, according the Equation (2). The process is repeated n times for each instance
as a random number between 0 and 1, according the Equation (2). The process is repeated n times for each instance ![]() from the P set, where n = b/100, and b is a parameter that defines the percentage of oversampling required to balance the dataset.
from the P set, where n = b/100, and b is a parameter that defines the percentage of oversampling required to balance the dataset.
![]() (2)
(2)
Figure 1 shows the SMOTE process with k = 5. Starting from (a), there is an imbalanced dataset, where (−) belongs to majority instances, also known as negative instances, and (+) belongs to minority instances, also known as positive instances. In (b) The KNN selects 5 nearest neighbors from a minority instance![]() . In (c) one of the five nearest neighbors
. In (c) one of the five nearest neighbors ![]() is randomly selected. In (d) a new synthetic instance is generated with random attributes between
is randomly selected. In (d) a new synthetic instance is generated with random attributes between ![]() and
and![]() . The process is repeated for every minority instance (+) from the subset P.
. The process is repeated for every minority instance (+) from the subset P.
An extensive comparison of several oversampling and undersampling methods was performed in [23] . The authors concluded the SMOTE combined with Tomek Links [24] and ENN methods [8] presented better performance in 50% of the experiments. Nevertheless, the SMOTE algorithm alone had better performance in 16% of the cases, and in most of the cases, it presented similar results in terms of AUC, if compared with the combined methods.
According the experiments conducted in [25] , one of the weaknesses of SMOTE lies in the fact all the positive instances acts as a base for synthetic instance generation. The authors argue such strategy doesn’t take into account that not always a homogeneous distribution of synthetic instances is applicable to an unbalancing problem; as such practice could cause overfitting and class overlapping. Another weakness reported is the result variance, caused by the random characteristics existing in some points of the algorithm.
2.3. Edited Nearest Neighbor Rule (ENN)
The ENN method proposed by [8] , removes the instances of the majority class whose prediction made by KNN method is different from the majority class. So, if an instance ![]() has more neighbors of a different class, this instance
has more neighbors of a different class, this instance ![]() will be removed. The ENN works according to the steps below:
will be removed. The ENN works according to the steps below:
1. Obtain the k nearest neighbors of![]() ,
,![]() ;
;
2. ![]() will be removed if the number of neighbors from another class is predominant;
will be removed if the number of neighbors from another class is predominant;
3. The process is repeated for every majority instance of the subset N.
According to the experiments conducted in [26] , the ENN method removes both the noisy examples as borderline examples, providing a smoother decision surface.
2.4. Neighbor Cleaning Rule (NCL)
The Neighbor Cleaning Rule (NCL) proposed by [9] , consists in improving the ENN method for two-classes problems in the following way: for each example![]() , find its k = 3 nearest neighbors. If
, find its k = 3 nearest neighbors. If ![]() belongs to the majority class and there is a prediction error related to its nearest neighbors,
belongs to the majority class and there is a prediction error related to its nearest neighbors, ![]() will be removed. If
will be removed. If ![]() belongs to the minority class and there is a prediction error related to its nearest neighbors, the nearest neighbors belonging to the majority class will be removed.
belongs to the minority class and there is a prediction error related to its nearest neighbors, the nearest neighbors belonging to the majority class will be removed.
2.5. Random Sampling
This is one of the simplest strategies for data sets adjusting, and basically consists in the random removal (undersampling) and addition (oversampling) of instances. For oversampling, instances of the positive set P are randomly selected, duplicated and added to the set T. For undersampling, the instances from negative set N are randomly selected for removal.
Although both strategies have the similar operation and brings some benefit than simply classifying without any preprocessing [1] [9] , they also introduce problems in learning. For the instances removal, there is the risk of removing important concepts related to the negative class. In the case of adding positive instances, the risk is to create over adjustment (overfitting), i.e., a classifier can construct rules that apparently are precise, but in fact cover only a replicated example.
2.6. Class Overlapping Problem
According the experiments of [3] , the low classification performance on imbalanced datasets is not associated only to the class distribution, but is also related to class overlapping. The authors concluded that normally in highly skewed datasets, the problem of “needle in the haystack” comes together with a class overlapping problems.
2.7. Evaluation Measures
In supervised learning, it is necessary to use some measure to evaluate the results obtained with a classifier algorithm. The confusion matrix from Table 1, also known as contingency table, is frequently applied for such purposes, providing not only the count of errors and hits, but also the necessary variables to calculate other measures.
The confusion matrix is able to represent either two class or multiclass problems. Nevertheless, the research and literature related to imbalanced datasets is concentrated in two class problems, also known as binary or binomial
problems, which the less frequent class is named as positive, and the remaining classes are merged and named as negative.
Some of the most known measures derived from this matrix are the error rate (3) and the accuracy (4). Nevertheless, such measures are not appropriated to evaluate imbalanced datasets, because they do not take into account the number of examples distributed among the classes. On the other hand, there are measures that compensate this disproportion in their calculation. The Precision (5), Recall (8) and F-Measure [27] are appropriated when the positive class is the main concern. The G-Mean, ROC and AUC are appropriated when the performance of both classes (positive and negative) are important.
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
In this work, both classes are considered as equal importance, therefore, the measures G-Mean and AUC will be used to evaluate the experiments.
The G-Mean [5] verifies the performance in both classes, taking into account the distribution between them, by computing the geometric average between the true positives and true negatives (6).
![]() (6)
(6)
The Receiver Operating Characteristics (ROC) chart, also denominated ROC Curve, has been applied in detection, signal analysis since the Second World War, and recently in data mining and classification. It consists of a two dimensions chart, were the y-axis refers to Sensitivity or Recall (7), and the x-axis calculated as 1-Especificity (8). According to [6] there are several points in this chart that deserve attention. By analyzing this chart it is possible to identify not only the classifier performance, but also to deduce some classifier behaviors like: conservative, aggressive, or aleatory.
![]() (7)
(7)
![]() (8)
(8)
The AUC measure (9) synthetizes as a simple scalar the information represented by a ROC chart, and is insensitive to class imbalance problems.
![]() (9)
(9)
where ![]() is the normal cumulative distribution,
is the normal cumulative distribution, ![]() is the Euclidean distance between the class centroids of two classes, and
is the Euclidean distance between the class centroids of two classes, and![]() , and
, and ![]() are the standard deviation from the positive and negative classes. An algorithm to calculate AUC is also provided in [6] .
are the standard deviation from the positive and negative classes. An algorithm to calculate AUC is also provided in [6] .
3. Proposed Method: KNN-Und
The KNN-Und method works removing instances from the majority classes based on his k nearest neighbors, and works according to the steps below:
1. Obtain the k nearest neighbors for![]() ;
;
2. ![]() will be removed if the count of its neighbor is greater or equal to t;
will be removed if the count of its neighbor is greater or equal to t;
3. The process is repeated for every majority instance of the subset N.
The parameter t defines the minimum count of neighbors around ![]() belonging to the P (minority) subset. If this count is greater or equal t, the instance
belonging to the P (minority) subset. If this count is greater or equal t, the instance ![]() will be removed from the training set T. The valid values of tare
will be removed from the training set T. The valid values of tare![]() and as lower t is, as aggressive is the undersampling. This algorithm can also be used in multiclass problems, as in the negative subset N can contain instances from several majority classes. The KNN-Und algorithm was developed as a preprocessing plug in in Weka platform [28] .
and as lower t is, as aggressive is the undersampling. This algorithm can also be used in multiclass problems, as in the negative subset N can contain instances from several majority classes. The KNN-Und algorithm was developed as a preprocessing plug in in Weka platform [28] .
If compared with ENN, the KNN-Und has a more aggressive behavior in terms of instance removal, because KNN-Und does not depend of a wrong prediction of KNN to remove an instance![]() . KNN-Und only acts in the class overlapping areas, because an instance from majority class only will be removed if a number t of instances from other classes are present in its neighborhood. In the cases that an instance of the majority class is not surrounded by t instances of other classes, that instance will not be removed. This situation only occurs in non-overlapping areas. Despite this behavior, in our experiments t = 1 was kept in most of the cases, because the KNN-Und only acts in overlapping areas. The nonoverlapping areas, which are far from the decision surface are kept untouchable. This explains why the KNN-Und can also be used to solve the class-overlapping problem, which is commonly associated with imbalanced datasets [3] . Nevertheless, in highly skewed problems the KNN-Und is not efficient to balance the dataset. In these cases, the combination of KNN-Und with another sampling method could improve the results.
. KNN-Und only acts in the class overlapping areas, because an instance from majority class only will be removed if a number t of instances from other classes are present in its neighborhood. In the cases that an instance of the majority class is not surrounded by t instances of other classes, that instance will not be removed. This situation only occurs in non-overlapping areas. Despite this behavior, in our experiments t = 1 was kept in most of the cases, because the KNN-Und only acts in overlapping areas. The nonoverlapping areas, which are far from the decision surface are kept untouchable. This explains why the KNN-Und can also be used to solve the class-overlapping problem, which is commonly associated with imbalanced datasets [3] . Nevertheless, in highly skewed problems the KNN-Und is not efficient to balance the dataset. In these cases, the combination of KNN-Und with another sampling method could improve the results.
The KNN-Und can be considered a very simple algorithm, and has the advantage to be a deterministic method, since different of other methods, there is no random component. In the literature review, only one study [29] has mentioned a similar methodology and application so far, but the results published previously demonstrated this alternative was not very well exploited at that time.
4. Experiments
In this section, the experiments to validate the applicability of KNN-Und are conducted. The Table 2 depicts the 33 datasets prepared for the experiments, ordered by imbalance rate (IR) [30] , which is the rate between the quantity of negative and positive instances. All the 33datasets are originated from UCI machine learning repository [31] . For the data sets with more than two classes, one or more classes with fewer examples were selected as the positive class, and collapsed the remainder as the negative class. The datasets were balanced with KNN-Und and submitted to a classifier, then the evaluation measures were compared with three methods based on KNN: SMOTE [7] , ENN [8] , NCL [9] , and the random undersampling method. The performance of KNN- Und was also compared with the published results of two other studies [10] [11] . All the algorithms tested in this work were implemented in Weka platform [28] .
In all datasets and algorithms that uses KNN, the parameter k was determined according to (1). The parameter t was adjusted in order to control the undersampling level with KNN-Und method, and in most of datasets with IR < 2, this parameter was set to t > 1 to control the excessive undersampling. The Table 2 shows the values of k and t for each dataset, and the respective under sampling effect of KNN-Und on the negative (majority) class and resulting IR. The parameters for SMOTE and Random Undersampling methods were adjusted to obtain a balanced class distribution. The ENN and NCL methods do not have a balancing control parameter.
The classification results in terms of AUC and G-Mean are presented in Table 3 and Table 4, respectively.
Those tables show the results averaged over 10 runs and the standard deviation between parentheses for the 33 datasets.
The classification results in terms of AUC with KNN-Und data preparation were compared with our previous work [10] . This paper proposed a Genetic Algorithm (GA) as an oversampling method, with the aim to evolve sub regions filled with synthetic instances to adjust imbalanced datasets. To reproduce here the same experiments conditions as before, the classifier used is the C4.5 decision tree algorithm [32] , with 25% of pruning and 10-fold cross validation. The Euclidean distance was used for numeric attributes, and the superposition distance for nominal attributes [17] [18] .
The same experiment setup was applied forC4.5 classifier without balancing (as a baseline comparison) and for the others balancing methods: SMOTE, ENN, NCL and Random Undersampling. The last columns of Table 3 and Table 4 presents the results of the proposed balancing method, KNN-Und, with C4.5 and 1-NN classifier.
![]()
Table 2. Datasets ordered by IR before balancing with KNN-Und and the respective effect after KNN-Und.
![]()
Table 3. Classification results―AUC.
![]()
Table 4. Classification results―G-mean.
This last classifier was included to make a comparison with the evolutionary algorithm EBUS-MS-GM developed in [11] .
The best result for each dataset is marked in bold.
Analyzing the AUC results in Table 3, it can be observed the KNN-Und with C4.5 algorithm outperformed in 19 of 33 datasets and had one dataset with equal result, if compared with the results of four different sampling methods. If compared with our previous results published in [10] , the KNN-Und outperformed in 11 of 15 datasets.
Figure 2 illustrates the results of AUC using the balancing methods with C4.5 classifier for the 33 datasets. It shows the AUC values of KNN-Und (in green) at the top, or nearby, in all datasets.
The results in terms of G-Mean (Table 4) shows that the KNN-Und outperformed in 20 of 33 datasets, and one dataset with equal result. Different of GA, SMOTE and Random Undersampling methods, the KNN-Und, C4.5, ENN, and NCL have a deterministic behavior, which lead to most stable results with standard deviations equals to 0. The second best results were obtained with NCL algorithm, but an excessive undersampling was observed in datasets with IR < 2, which led to G-Mean values of 0.
Table 5 summarizes the count of the best results of the balancing methods with C4.5 classifier in terms of AUC and G-Mean. The KNN-Und has the highest scores.
These results can be explained by the fact that KNN-Und acts removing instances from the majority classes and at the same time cleaning the decision surface, reducing the class overlapping. Figure 3 and Figure 4 show the scatter plot of datasets EcoliIMU, and Satimage4, before and after the balancing methods. The points in blue belong to the majority class, the points in red to the minority class. These plots show the behavior of the methods, as described previously. The SMOTE algorithm performs a homogeneous distribution of synthetic instances around each positive instance. The ENN removes negative instances around the positive instances, and KNN-Und performs a more aggressive removal of negative instances in the decision surface region.
G-Mean and AUC values were not published by dataset for the evolutionary algorithm EUB-MS-GM in [11] , so another comparison was done with the available results, that is, the average and standard deviation of G- Mean and AUC for the 28 evaluated datasets. Table 6 compares the average results of KNN-Und and EUB-MS- GM methods. The KNN-Und results are at least 13 points higher than the EUB-MS-GM. It is not reasonable to do a comparison of standard deviations here, as the 28 datasets have independent results in both cases. One explanation for the obtained high values would be the 1-NN classifier used for comparison, that uses a decision boundary similar to KNN-Und, but the results for KNN-Und with C4.5 decision tree also had higher average values, showing that KNN-Und can also improve the classification results with other algorithms.
![]()
Figure 2. Comparison of classification with AUC after the balancing methods.
![]()
Table 5. Summary of the classification best results in terms of AUC and G-Mean between KNN-Und and other balancing methods using C4.5.
![]()
Table 6. Average of G-Mean and AUC from 28 the datasets used in [11] .
5. Conclusions
This work presented a proposal of an algorithm, KNN-Und, to adjust datasets with imbalanced number of instances among the classes, also known as imbalanced datasets. The proposed method is an undersampling method, and is based on KNN algorithm, removing instances from the majority class based on the count of neighbors of different classes. The classification experiments conducted with the KNN Undersampling method on 33 datasets outperformed the results of other six methods, two studies based in evolutionary algorithms and the SMOTE, ENN, NCL and Random Undersampling methods.
The good results obtained with KNN Undersampling can be explained by the fact that KNN-Und acts removing instances from the majority classes, reducing this way the “needle in a haystack” effect, at the same time, cleaning the decision surface, reducing the class overlapping and removing noisy examples. These results indicate that the simplicity of KNN can be used as a base for constructing efficient algorithms in machine learning and knowledge discovery. They also show that the selective removal of instances from the majority class is an interesting way to be followed rather than to generate instances to balance datasets. This issue is important nowadays as the datasets are approaching the size of petabytes with big data, and retaining only the representative data can be better than creating more data.