Finite Element Modeling of Stamp Forming Process on Thermoplastic-Based Fiber Metal Laminates at Elevated Temperatures ()
1. Introduction
As a response to the trend of reducing CO2 emissions, research on lightweight construction based on alternative materials has become the most promising strategy undertaken by automobile manufacturers. Fiber metal laminate (FMLs) is among the most innovative lightweight materials, which is created by bonding fiber-reinforced composite laminate to metal sheets, designed to merge the formability of metal and advanced properties of composite materials into one material system [1]-[3].
Experiments on forming of FMLs have been conducted to obtain a selective combination of forming parameters for obtaining better part quality. Works of Mosse et al. [4] indicated that by pre-heating the blank, die and blank-holder to a specific temperature, FMLs show less shape error and delamination. The interaction between forming temperature and blank-holder force was also found to have a close relationship to failure [5]. The mechanism of the interaction among forming factors was further clarified by the study on major strain and strain ratios evolution affected by sets of different temperature, binder force and feed rate [6]. Simulation-wise, Mosse et al. [7] investigated the composite-metal interaction by modeling the crystallization behavior of the interlayer adhesive and its shear stress transfer characteristics. The modeling of Davey et al. [8] accurately simulates the evolution of strain as observed in experimental trials. But influence of forming temperature on the forming mode of constituent layers of FMLs is yet to be found, which has inspired this work.
2. Modeling
2.1. Material Prosperities of Constitute Layers
Two types of fiber-reinforced thermoplastics, Curv® and Twintex®, are modelled as the core layer of FMLs, with mechanical properties listed in Table 1. Curv® is a self-reinforced polypropylene that has a plain woven structure of polypropylene fiber bundled in polypropylene matrix. Twintex® is a fiber-reinforced polypropylene with a balanced 2/2 twill weave of glass fibers. They exhibit diverse features when they are deformed. Curv® shows good ductility and high strain value at failure, whereas Twintex® is stiffer and fails at a lower strain value.
The constitutive equations employed for Curv® at different forming temperature [9] is described by
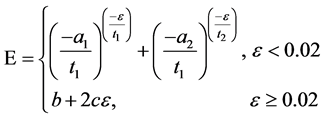 (1)
(1)
where ε is instantaneous strain and



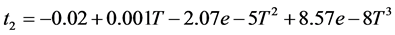
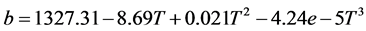
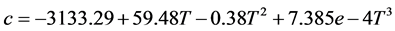
Similarly, the constitutive equation for Twintex® is described by
 (2)
(2)
where ε is instantaneous strain and
![]()
Table 1. Mechanical properties of Curv®, Twintex® and Aluminum alloy 2024-T3.




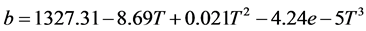

2.2. Contact Interface
The interfacial friction between the aluminum and composite layers is simulated based on the thermal property of a hot-melt film, Gluco®, which used to bond the aluminum and composite layers. The melting and crystallization temperature of Gluco® are 140˚C to 160˚C and 102˚C to 118˚C respectively [4]. Experiment conducted by Mosse et al. [7] indicated that at temperatures below 135˚C, the bond possesses low shear strength to resist interfacial displacement and if displacement does occur, it will result in the permanent bond damage. Above 135˚C any displacement will have a much less catastrophic effect on the final bond strength and below 100˚C the bond is strong enough to resist shear stresses.
A user-defined interface subroutine integrated temperature influence to the shear strength of the bond between the layers was developed, shown in Figure 1. At each time interval, the bonding shear strength is calculated based on the nodal temperature and compared to real-time tangential stress. If the stress value surpasses the shear strength below the threshold temperature, a failure event is recorded at the specific node. The bonding at this node is then released, allowing the adjacent surfaces to slide. If the failure occurs above the threshold temperature, the state of the bond is suspended and will be checked again when the temperature is lower than 135˚C. Given the critical temperature, 100˚C and 150˚C were chosen as forming temperatures for modeling, in order to investigate the contribution of the two types of behaviors.
![]()
Figure 1. Flow diagram of interfacial friction routine between FML laminates [7].
2.3. Finite Element Analysis Setup
The setup of round-bottom cylindrical cup test was used for modeling. The FML models were composed of three circular layers, which have uniform initial diameter of 180mm before the stamping process. The top and bottom aluminum layers are 0.5 mm in thickness, while the composite core layer has a thickness of 1 mm.
The fully integrated quadrilateral shell element, in cooperation with full projection of warping stiffness was used to enhance the in-plane bending and improving the stability and accuracy of the numerical result.
3. Modeling Result
The through-thickness stains were collected from three points of interest on the blank, as shown in Figure 2; 1) Point 1 at the pole of dome, 2) Point 2, 40 mm from the pole along the fiber-direction, 3) Point 3, 40 mm along 45˚ direction to the fiber orientation from the pole. They were compared to their counterparts in monolithic aluminum alloy. Since temperature has very limited effect on the strain path of aluminum alloy subjected to sheet forming [7], data of forming at 25˚C is adopted for comparison.
3.1. Strain Path at Point 1―The Pole
Forming mode at Point 1 is biaxial stretching, shown in Figure 3 and Figure 4. Only magnitudes of strains are changed by raising the temperature, while the strain ratio remains the same as that of the FML at room temperature. At 100˚C, softened matrix promotes the flow of material in the composite layer. This enhances the ductility of Curv®/Twintex®, making the strain values through the thickness close to or even lower than those of monolithic aluminum. However, at 150˚C, the magnitudes of strain in both Curv®-FMLs and Twintex®-FMLs dramatically surpass that of monolithic aluminum alloy.
3.2. Strain Path at Point 2―Side-Wall along Fiber Direction
At room temperature, material flow within the composite layers is strictly confined by the weave of the fibers, which transforms the FMLs from drawing to plane strain region. By increasing the forming temperature and thereby increasing the flow of matrix in fiber-reinforced layers, the forming performance at Point 2 is noticeably improved, shown in Figure 5 and Figure 6. For Curv®-FMLs, the strain path of Curv® layer shows obvious
![]()
Figure 2. Points of interest at pole and on side-wall.
![]()
![]()
![]()
Figure 3. Strain diagrams of Point 1 of Curv®-FMLs at (a) 25˚C; (b) 100˚C and (c) 150˚C.
![]()
![]()
![]()
Figure 4. Strain diagrams of Point 1 of Twintex®-FMLs at (a) 25˚C; (b) 100˚C and (c) 150˚C.
![]()
![]()
![]()
Figure 5. Strain diagrams of Point 2 of Curv®-FMLs at (a) 25˚C; (b) 100˚C and (c) 150˚C.
![]()
![]()
![]()
Figure 6. Strain diagrams of Point 2 of Twintex®-FMLs at (a) 25˚C; (b) 100˚C and (c) 150˚C.
tendency of drawing at 100˚C, while at 150˚C, the strain paths of Curv® show great deviation from that of aluminum skin layers, which indicates severe interply slide or even delamination. For Twintex®-FMLs, stiffness of the glass fibers constrains the matrix flow and does not allow so much drawing at 100˚C, but the magnitude of strains in each layer is significantly decreased compared to room temperature. At 150˚C, as the matrix melts and flows more easily, the forming mode of aluminum layer is even less constrained and shows similar strain path to that of monolithic aluminum.
3.3. Strains Path at Point 3―Side Wall along 45˚ to Fiber Direction
Shearing strain dominates the forming behavior at Point 3 of the FMLs at room temperature. This pattern is also exhibited at elevated temperatures. At 100˚C, the strain paths of all three layers in Curv®-FMLs almost coincide with that of the monolithic aluminum alloy, shown in Figure 7(b), which indicates the performance of Curv®-FMLs is nearly the same as that of the monolithic aluminum alloy. For Twintex®-FMLs, shown in Figure 8, forming mode of the aluminum layers is close to drawing at 150˚C. However, the Twintex® layer still remains in the plane strain region, mainly due to the poor ductility of glass fiber.
4. Conclusion
Due to the inherent material properties of fiber-reinforced polypropylene and adhesive bonding, elevation in forming temperature significantly alter the stiffness and shear modulus of the composite laminate. Flow of matrix material is promoted, larger rotation angle of fiber at intersection is allowed, which influences the behavior of adjacent aluminum layer as well. Curv®-FMLs achieved similar forming performance to monolithic
![]()
![]()
![]()
Figure 7. Strains diagram of Point 3 of Curv®-FMLs at (a) 25˚C; (b) 100˚C and (c) 150˚C.
![]()
![]()
![]()
Figure 8. Strain diagrams of Point 3 of Twintex®-FMLs at (a) 25˚C; (b) 100˚C and (c) 150˚C.
aluminum at 100˚C. This is a strong indication that FMLs can have equivalent formability to monolithic metal alloy, with an optimal combination of material type, forming temperature and other relevant forming parameters.