Automatic Modification of Local Drilling Holes via Double Pre-Assembly Holes ()
1. Introduction
According to investigations, almost seventy percent of fatigue related aircraft crashes result from fastener structures, while eighty percent of those fatigue cracks occurred at fastener holes. Since damaged system can be replaced after the accident, the whole life span of an airplane directly depends on each single unit of structure [1]. Though traditional manual drilling can adapt to complicated situations while obtains low cost and flexible operation, it also goes along with low efficiency and unstable quality [2]. Moreover, the increasing amount of fastener holes in modern planes along with the involvement of intractable materials like titanium alloy and carbon fiber, both exacerbate the difficulty of manufacturing of airplane fastener holes. However, the manual drilling process can no longer guarantee the quality of them [3] [4].
Under such circumstances, automatic assembly has been widely investigated and used in practice to increase the efficiency in massive production [5]. As a result, automatic drilling and riveting system has become to play a much more important role in airplane assembly, like the G86 and G14 drilling and riveting system of American Gemcor. In addition, light and flexible drilling system has also gained more attention in companies like Boeing and Airbus during recent years. For example, the drilling robot called ONCE (One-sided Cell End effector) has been successfully applied to the assembly line of ailerons of Boeing F/A-18E/F [6]. To enhance the accuracy of drill positioning, many efforts have been focused on automatic hole-drilling in the community. For instance, reference [7] built up a closed loop feedback of drilling system by laser tracking instruments.
Recently, automatic assembly system has gained many benefits from offline programming. During the process of automatic drilling, model parameters like hole’s position and normal direction could be obtained from CAD modules of structures. However, chances are big that the CAD does not match the desired model of structures perfectly, which can further result in false positioning of fastener holes. As a result, post-modifications need to be made in practice. Instruments like laser tracking can produce accurate measurements but it is too expensive and complicated to use in the assembly of simple structures by comparison. For visual inspecting system, we have to move the system actively during measuring process, which could be highly unstable and inaccurate [8].
In practice, a great amount of airplane components is simple structural elements. They do not need high standard of position accuracy but as long as a fair position of intersecting point and reasonable hole margin. Given the limits of current measurements and assembly structures, we often measure the offset between positions of pre-assembly holes and their theoretical values. The average of those offsets is then used to modify the assembly. However, such modification is unstable and inaccurate in practice.
In this paper, we present a novel method for holes modification. Based on the online inspecting coordinates of the two pre-assembly holes in the drilling area and their ideal values from CAD modules, we calculate the transformation matrix between two systems. With the transformation matrix, the locations of holes along the line where two pre-assembly holes lie on could be obtained.
2. Modification of Straight Drilling on Single Degree Skin
A common body of airplane consists of vertical elements (long truss and truss beam), horizontal units (the frame and rib) and coverings. We assemble the plane body or wing panel by riveting structural elements like coverings and long truss. The most typical scenario is straight drilling on single degree skin, as shown in Figure 1.
For the single curvature covering structure in Figure 1, we can modify the holes by double assembly holes, as indicated in Figure 2. We use two pre-assembly holes to modify the drilling holes within a certain area. The two pre-assembly holes are often set at the opposite endpoints which is perpendicular to long truss. The distance between the two holes is within 300 - 600 mm.
![]()
Figure 1. Assembly structure of single degree.
![]()
Figure 2. A diagram of single degree skin.
Suppose the coordinate system of automatic drilling and riveting machine is denoted S with origin O. T1 and T2 are the theoretical coordinates of the two pre-assembly holes: 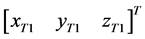 and
and ,
, 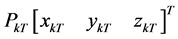 (k = 1, 2, 3 … N) are coordinates of the holes within the area, which are indicated as red dots in Figure 2, N is the overall number of them. Let A1 and A2 denote the realistic coordinates of two pre-assembly holes:
(k = 1, 2, 3 … N) are coordinates of the holes within the area, which are indicated as red dots in Figure 2, N is the overall number of them. Let A1 and A2 denote the realistic coordinates of two pre-assembly holes: 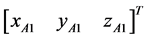 and
and ,
,  (k = 1, 2, 3 … N) are the realistic coordinates for the N holes, as indicated as blue dots accordingly in Figure 2.
(k = 1, 2, 3 … N) are the realistic coordinates for the N holes, as indicated as blue dots accordingly in Figure 2.
In practice, we aim to revise PkA by PkT. so that the exchangeability, synchronization and structural strength of each element can be assured. The real coordinates of T1, T2 and PkT can be obtained by offline programming. We can also measure the locations of A1 and A2 through the executor by the end of automatic riveting machines. Thereafter, we can modify the drilling holes of single curvature covering as follows [9]:
1) Compute the vector 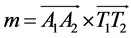 and normalize it as
and normalize it as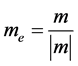 ,
,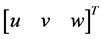 .
.
2) Calculate the angles between ideal and real line of drilling holes from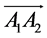 ,
,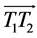 .
.
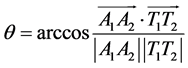
3) Rotate 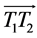 along by
along by 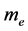 with
with 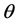 so that
so that ![]() coincides with
coincides with![]() . The rotation equations are
. The rotation equations are
![]() (2)
(2)
4) Compute the realistic coordinates of PkA with the ideal locations PkT
![]() (3)
(3)
3. Simulation and Validation
3.1. Modification of Rotations
Provided a pair of ideal and real coordinates as T1 (1620, 2100, 800), T2 (1930, 2491.7908, 820), A1 (1621.8147, 2100.9084, 799.3500), A2 (1931.6375, 2491.5988, 832.9039). The distance between the two points is 500 mm.
Due to location errors during pre-assembly holes and inevitable measurement errors in instruments, we have to add a certain degree of perturbation errors to A1 and A2. The location precision of most holes on the single curvature covering is simulated as 0.2 mm. In this case, the perturbation error is 0.3 mm accordingly.
The resulting vectors are ![]() (310, 391.7908, 20) and
(310, 391.7908, 20) and ![]() (309.8227, 390.6904, 33.5539).
(309.8227, 390.6904, 33.5539). ![]() (0.7846, −0.6187, −0.0400). Assuming the rotation angle be
(0.7846, −0.6187, −0.0400). Assuming the rotation angle be ![]() and perturbation
and perturbation ![]() 0.29 mm, we place
0.29 mm, we place
every holes along the line of two pre-assembly holes with interval 100 mm. Then we compute the coordinates of each drilling hole with 1000 iterations. The results with the 5 percent maximum eliminated are presented in Table 1.
As in Table 1, the precision before modification is 1 mm. while this number is reduced to maximum 0.2024 after modified with our straight line based single curvature method. We can also see that the location errors are dramatically reduced in Figure 3. In fact, the location error of our method main depends on the positioning error of the two pre-assembly holes.
3.2. Modifications of Translations
Provided another pair of ideal and real coordinates as T1 (1620, 2100, 800), T2 (1930, 2491.7908, 820), A1 (1621.9832, 2100.9917, 799.4669), A2 (1931.9782, 2492.7892, 819.4439). The perturbation is 0.29 mm. The
resulting vectors are ![]() (310, 391.7908, 20)
(310, 391.7908, 20) ![]() (309.9950, 391.7975, 19.9769) and
(309.9950, 391.7975, 19.9769) and ![]() (−0.7486,
(−0.7486,
0.5755, 0.3292). The rest settings are as same as in the last section. We also compute the coordinates of each drilling hole with 1000 iterations. The results with the 5 percent maximum eliminated are presented in Table 2.
As in Table 2, when ![]() is translated from
is translated from![]() , the precision is around 0.01 mm while the maximum error is 0.1999 mm. Figure 4 also demonstrates that the positioning accuracy is greatly increased after our modification, whose main factor is also the location accuracy of pre-assembly holes.
, the precision is around 0.01 mm while the maximum error is 0.1999 mm. Figure 4 also demonstrates that the positioning accuracy is greatly increased after our modification, whose main factor is also the location accuracy of pre-assembly holes.
![]()
Figure 3. Errors in different situations of rotations.
![]()
Table 1. Errors before and after modification of rotations.
![]()
Figure 4. Errors in different situations of translations.
![]()
Table 2. Errors before and after modification of translations.
3.3. Validation
We further validate the proposed algorithm upon the gantry type automatic drilling and riveting system at Nanjing University of Aeronautics and Astronautics, as shown in Figure 5. To reduce the effects of elements’ shape error, we drill holes on three 600 mm × 600 mm flat aluminum coupons to do the experiment. Every coupon has 4 pre-assembly holes. In order to verify the feasibility and check the accuracy of the modification method, the experiment adds an agitation less than 0.2 mm to each pre-assembly hole.
The experimental scheme is shown in Figure 6, and the experimental steps are as follows:
1) Translate the coupon 3 mm with T1 and T4 as a reference, and get the holes in column A;
2) Modify the positions of the drilling holes with T2 and T3 as a reference, and get the holes in column C;
3) Rotate the coupon ![]() with T1 and T2 as a reference, and get the holes in column D;
with T1 and T2 as a reference, and get the holes in column D;
4) Modify the positions of the drilling holes with T3 and T4 as a reference, and get the holes in column B;
The result of experiment is measured by the triple-coordinates instruments. Its model is Mistral 1070705, and its measurement accuracy can reach 3 μm. The measurement result and the simulation remain consistent, and the former is a little larger, which is acceptable. It turns out that, when the position accuracy of pre-assembly holes is 0.3 mm, the precision of drilling holes can get 0.2 mm after modified with the proposed modification method.
4. Conclusions
In this article, an online modification method is proposed for drilling holes based on double pre-assembly holes. The main conclusions are as follows:
1) Compared to traditional revisions, it is more robust in that it can guarantee the drilling accuracy along the line determined by the pre-assembly holes. With 0.29 mm precision of pre-assembly holes, the drilling accuracy is less than 0.2 mm with our modification algorithms.
2) The proposed method measures the local area of structural elements based on online programming, which avoids the reliance on integral precision of the whole structures. It also reduces the financial cost of modification
![]()
Figure 5. Gantry type automatic drilling and riveting system.
process by waiving the use of large instruments like laser tracking system.
3) With the proposed algorithm, the technician is able to optimize the arrangements of pre-assembly holes on structural units so that they can adapt accuracy of the pre-assembly holes to different manufacturing conditions.
NOTES
*Corresponding author.