1. Introduction
Buoyancy induced by natural convection phenomenon with smooth and rough walls has been a subject of many research studies for decades being rich in its applications [1]. Its significance is further enhanced because of its incorporation in passive safety systems of Small Modular Reactors (SMRs) and advanced generations of nuclear reactors [2]. It has remarkable applications from micro scale to macro scale devices, and especially in nuclear industry like removal of decay heat during accident and shutdown phases, nuclear reactor design and safety, reactor insulation, design of radioactive waste containers etc. [3]. Heat transfer through natural convection from vertical surfaces in the presence of some sort of roughness came across in many applications [4]. Therefore, a better understanding is essential for natural convection heat transfer phenomenon in the presence of roughness that can result in efficient energy systems.
Square cavities with smooth walls and walls with some sort of partitions or fins has been studied for decades to enhance the heat transfer during natural convection. A detailed experimental, theoretical, and numerical analysis are present in the literature [1] [5] [6]. Bajorek and LIyod [7] performed experimental studies to analyze the effects of an insulated rectangular partition present on the bottom insulated wall in a square cavity. They used air and carbon dioxide as working fluid in the range of Grashof number (Gr) from 1.7 × 105 to 3.0 × 106. They found a decrease in the heat transfer from 12 to 21 percent in the presence of partitions as compared to a smooth cavity.
Anderson and Bohn [8] conducted experimental studies to investigate the effects of square roughness elements on the heat transfer in a cubical cavity. They used water as a working fluid. They found an increase in the average heat transfer up to 15 percent at 3.3 × 1010. They also observed an increase in the local heat transfer up to 40 percent. Bhavnani and Bergles [4] experimentally studied the effects of a sinusoidal wavy surface on the heat transfer during natural convection. They observed an increase in the heat transfer approximately 15 percent as compared to a smooth wall.
Shakerin et al. [9] performed experimental and numerical studies to analyze the role of rectangular roughness elements in a square cavity. They used dye flow visualization technique and numerical approach using finite difference method. They incorporated a single and double rectangular roughness elements by varying spacing between them on isothermal vertical walls, while horizontal walls were adiabatic. They found an increase in the average heat transfer up to 12 percent compared to a smooth cavity for a single roughness element and 16 percent with double roughness elements. Moreover, they concluded that increase in the heat transfer is counter balanced by the decrease in the velocity due to the presence of roughness elements.
Amin [10] utilized a finite element based computational code NACHOS to study natural convection in the presence of rectangular roughness elements in a square cavity. He introduced the roughness elements on the bottom isothermal wall with vertical walls as insulated. He used a fluid of Pr number 10 and varied amplitude and spacing between the roughness elements. He observed an increase in the heat transfer of 57 percent at Ra number 2 × 103 and a decrease of 61 percent at Ra number 3 × 104.
Natural convection is an integral part of passive safety systems in SMR and advanced reactors. Carrilho et al. [11] numerically studied the role of two-dimensional artificial surface roughness in a fuel rod bundle of pressurized water reactor (PWR) using finite element method computational tool. They observed an enhancement in the heat transfer at re-attachment point. Carrilho and Khan [12] also performed numerical studies to investigate the role of parallel rib-type roughness effects on convective heat transfer and flow resistance. They concluded that roughness cause an increase in the flow resistance. An increase in the critical heat flux (CHF) was also found in water-cooled reactors in the presence of grooved or ribbed tubes [13]. Meyer et al. [14] [15] performed many studies to analyze two and three dimensional roughness elements in gas cooled reactors and light water reactors, they found an increase in the heat transfer and friction factor.
Previous experimental and computational studies performed focused on the role of partitions, surface roughness, and fins, in a square cavity. But studies of buoyancy induced natural convection was limited to rectangular and square shaped roughness elements in a square cavity. Therefore, in the present research, sinusoidal roughness elements were introduced on the isothermal vertical wall of a square cavity. Effects of roughness elements were observed by calculating the average heat transfer. Besides, the traditional numerical techniques, the present study was performed by using a single relaxation time Bhatnagr-Gross and Krook (BGK) model of lattice Boltzmann method (LBM) for a Newtonian fluid of Prandtl number 1.0 in a two-dimensional square cavity. During this study, Ra number was explored from 103 to 106 for a rough square cavity. Effects of the sinusoidal roughness elements were analyzed by comparing average Nu, isotherms, and streamlines with smooth cavity.
2. Mathematical Modelling
The numerical simulations for natural convection phenomenon were performed by using a single relaxation time BGK model of LBM in a two-dimensional square cavity with length “L” and height denoted by “H”. A Newtonian fluid having Pr number 1.0 was considered in the present study. The simulations explored the range of Ra number from 103 to 106. The roughness was introduced in the form of sinusoidal roughness elements having a dimensionless amplitude (A = h/H) equal to 0.1. The number of roughness elements was equal to 10 and were located on both the hot and cold walls simultaneously of a square cavity. The simulation geometry used in the present study is shown in Figure 1. The corresponding boundary conditions are also mentioned on correspond-
![]()
Figure 1. Simulation geometry for a rough square cavity.
ing walls. During this numerical experiment, the sinusoidal roughness elements were at the same boundary condition as corresponding vertical or isothermal walls of the cavity. Coupled momentum and energy equations were solved in a laminar flow region with assumption that viscous dissipation was negligible and fluid was assumed to be radiatively non-participating medium [10]. The coupling between Navier-Stokes and energy equation was made by using the Boussinesq approximations. All other physical properties were considered constant except the density, which was varying with temperature as shown in Equation (1) [16].
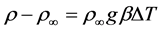 (1)
(1)
The dimensionless numbers and temperature used during the numerical simulations were given by following relations [16].
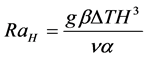 (2)
(2)
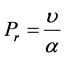 (3)
(3)
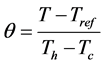 (4)
(4)
Here, Tref was mean or average temperature of both hot and cold vertical isothermal walls. Average heat transfer throughout the present study was quantified using the dimensionless number called the Nusselt number (Nu) by following relations [17]-[19] on isothermal walls and in the entire volume.
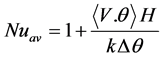 (5)
(5)
where “< >” showed that the quantity was averaged over entire fluid volume, Δθ is dimensionless temperature difference between hot and cold walls, “V” was vertical velocity component. The viscous dissipation term has been neglected as the frictional effects are negligible for laminar and small Mach number flow. Also, magnitude of viscous force is negligible for fluid having Pr ≤ 1 [1]. A single relaxation time based model of the LBM has been utilized for solution. The detailed description of this numerical approach is mentioned in references [20] [21].
3. Numerical Methodology
A single relaxation time Bhatnagr-Gross and Krook (BGK) model of LBM [21] has been used for last two decades as an alternate to traditional numerical techniques. LBM has achieved a great success in the last two decades in simulating fluid flow and heat transport phenomenon. It is a significant numerical tool in simulating single, and multiphase flow and heat transfer, condensation, evaporation, and other complex phenomenon in complex geometries [21]. This method was originated from a model of lattice gas automata (LGA), which solve dynamics of a hypothetical particle [22]. Although, LBM has achieved a great success in simulations of fluid flow and heat transfer problems, but still has some issues of numerical stability at high Ra number flows [23]. LBM has many advantages like: ease of algorithm, inherently suitable for parallel computing, easy treatment of complex boundary conditions as compared to other traditional numerical methods. In simulations based on LBM, Laplace equation is not required to be solved at every time step [20] [21]. Solution of both momentum and energy equations is performed independently by using two separate distribution functions. The energy equation was solved by considering temperature as a passive scalar [24] in five directions. Passive scalar approach assumes that temperature at macroscopic level behaves as passive scalar, if viscous dissipation and compression works are neglected [21]. In the present study, a well-established single relaxation time Bhatnagr-Gross and Krook (BGK) model of LBM was adopted, therefore, a detailed description is omitted, because of space limitations. However, reader is referred to Sukop and Thorne [21], Mohamad [20], and Yang et al. [25] for a detailed study of LBM and all models presented thus far.
In order to solve Navier-Stokes and energy equations, a standard D2Q9 model for velocity and D2Q5 for passive scalar has been used as shown in the Figure 2. An easy treatment of complex boundaries in LBM, is one of the most significant element which causes a great success for LBM [26]. Boundary conditions play a significant role in better convergence of a solution both at macro and micro level. In numerical simulations with LBM, we have to transform macro level boundary conditions which are suitable for both energy and momentum equations in solving with distribution functions [27]. No-slip boundary conditions were implemented at all solid walls and roughness elements, using an half-way or mid-plane bounce back scheme as illustrated in Mohamad [20] and Sukop and Thorne [21]. Thermal boundary conditions for isothermal or adiabatic walls are implemented as explained by Mohamad [20].
A computational algorithm based on a single relaxation time BGK model of LBM was first validated in to two steps. In the first step, grid independence study was performed at Ra number 104 for a smooth square cavity. The results for average Nu calculated using Equation 5, were compared with well-established previous benchmark studies conducted by Vahl Davis [28] as shown in the Table 1. In the second step, average Nu values for a smooth square cavity produced with present computational code were compared with Davis [28] as shown in the Figure 3.
![]()
Figure 2. D2Q9 and D2Q5 models of velocity and temperature respectively.
![]()
Table 1. Grid independence study for square cavity using average Nu.
![]()
Figure 3. A comparison of average Nu values for present and Vahl Davis [28].
A comparison of the average Nu values produced using the present computational algorithm with previous benchmark solution for a smooth cavity by Davis [28] showed that results can be considered grid independent and reliable with good accuracy.
4. Results and Discussion
Numerical study was performed to analyze the effects of sinusoidal roughness elements on both the hot and cold walls simultaneously. Sinusoidal roughness elements of dimensionless amplitude of 0.1 and number of elements equal to 10 were incorporated on isothermal walls. Many simulations were carried but only some significant results are reported here. Results are compared with a smooth cavity for average Nu, isotherms and streamlines to make a better analysis. Figure 4 shows a comparison between the average value of Nu for both the smooth and rough square cavities. The average heat transfer in the presence of the sinusoidal roughness elements present on the both walls was significantly affected.
Figure 4 shows that as Ra number was increased, the average value of Nu decreased. This decrease in Nu was observed to be more at higher Ra number as compared to lower. The maximum decrease in the average heat transfer was calculated to be equal to 23.33% at Ra number equal to 106. The decrease in the average heat transfer may be due to following: a reduction in the volume of fluid in the presence of roughness, a decrease in the effective distance between isothermal walls, and formation of eddies or vortices in the wakes of the roughness elements in the presence of roughness. When the sinusoidal roughness elements were introduced in the cavity, the effective distance between isotherms was decreased, this resulted in the decrease of average or effective Ra number. This decrease in Ra number may cause a decrease in the average heat transfer. Also, due to the presence of the roughness in the cavity of same dimensions as in case of smooth, volume of fluid was reduced. Heat transfer takes place from hot to cold wall through a medium, this decrease in the average volume of the fluid may cause a reduction in the average heat transfer in the cavity. Similar results were reported by Amin [10] [29].
Shakerin et al. [9] conducted experimental and numerical studies to analyze the effects of rectangular roughness elements in a square cavity. They observed a slight enhancement in the heat transfer, and concluded that addition in the average surface area for the heat transfer was larger as compared to enhancement in the heat transfer. Moreover, they reported that the presence of roughness elements hindered or obstruct the velocity flow in the cavity. This obstruction in the velocity may result in the decrease of the heat transfer. In the present simulations, twenty roughness elements were located on both the hot and cold walls in a square cavity, these roughness elements may cause a strong obstruction in the fluid flow, and hence resulted in the decrease of heat transfer.
Another significant factor that was observed during the present simulations was the formation of eddies or vortices in the interstices of the sinusoidal roughness elements. When Ra number was increased to 104, strong formation of eddies was observed with a size of equal to wake between roughness elements. This formation of eddies or vortices may cause a reduction in the average heat transfer. These eddies cause a detachment of fluid from the hot vertical wall of the cavity. This detachment from hot wall may play role in the heat transfer reduction [30]-[32].
In a differentially heated square cavity, fluid rises up along the hot wall and downward along the cold wall. No gain or loss occurs along the insulated horizontal walls. This behavior of fluid is shown in the figures below.
![]()
Figure 4. Average nu for smooth and rough square cavity.
Figures 5-7 show that streamlines both for a smooth and rough cavity for different Ra numbers. The presence of the sinusoidal roughness elements significantly affect the fluid behavior inside the cavity. Streamlines behavior in the smooth and rough cavities was almost same except the formation of eddies or vortices in the wakes of the roughness elements. At Ra number 104, strong eddies formation was observed along the entire hot and cold wall. The size of eddies were almost same as the size of wakes.
When Ra number was increased beyond the 104, eddies formation was altered. At Ra number 105, size of eddies or vortices as compared to eddies at Ra number 104, decreased comparatively. Also, eddies at bottom of hot wall and top of cold wall disappeared. Local recirculation of fluid in the center of rough and smooth cavity was almost same except a slight shrinking in the rough cavity. This shrinking may be due to the presence of the roughness elements. When Ra number was increased to 106, only a few eddies or vortices of very small size were observed at upper half of hot wall and lower half of the cold wall. The size was shrunk or decreased as compared to eddies at Ra number 104. The local recirculation in the central part was same as in the smooth cavity. The variation in the size and number of eddies formation in the wakes of the roughness elements may be due to variation in the magnitude of the velocity. At lower Ra < 104, due to weak buoyancy force, velocity is smaller in the cavity. Due to this small velocity, fluid may be trapped in the interstices of the roughness elements. But when Ra number is increased above 104, buoyancy force increased, and hence results in the increase of velocity within the cavity. Due to this increase in the velocity, fluid is swept away from the wakes of the roughness elements.
Thermal behavior of the Newtonian fluid was observed in the form of isotherms. The isothermal lines were drawn in the range 0 to 1 using dimensionless temperature. Both the smooth and rough cavity’s isotherms were reported for a better analysis. Figures 8-10 show the thermal behavior in both the smooth and rough cavity for different Ra number. The isotherms behave in the both cavities in almost same manner. At lower Ra number up to 104, due to weak buoyancy force, the stratification in the isotherms is almost same in both the smooth and rough cavity. The isotherms are parallel to peaks of the roughness elements in the rough cavity. At lower Ra number <104, no constriction of isotherms was observed in the wakes of the roughness elements.
When the Ra number was increased, constriction of isotherms was observed. As Ra number was increased to 105 and 106, which caused an increase the buoyancy force, the isotherms started shrinking towards the hot and cold walls. This behavior was same in both the smooth and rough cavities. The only difference observed, when the sinusoidal roughness elements were present on both walls simultaneously, isotherms constriction or density in the wakes of roughness elements increased with increase of Ra number above 104. Isotherms at the peaks of the roughness elements were parallel at higher Ra number. The stratification was same in both the smooth and rough cavities at Ra number 105, and 106. The isotherms in the central part or the core of the both cavities were almost parallel to horizontal walls. This horizontal orientation showed a strong domination of the conduction phenomenon in the central part. The shrinking of the isotherms towards the hot and cold walls also showed that effect of convection phenomenon were strong close to isothermal walls.
![]()
Figure 5. Streamlines for smooth and rough square cavity at Ra 104.
![]()
Figure 6. Streamlines for smooth and rough square cavity at Ra 105.
![]()
Figure 7. Streamlines for smooth and rough square cavity at Ra 106.
![]()
Figure 8. Isotherms for smooth and rough cavity at Ra 104.
5. Conclusion
A computational algorithm was developed using a single relaxation time BGK model of LBM to study the effects of the sinusoidal roughness elements on the thermal and hydrodynamic behavior of a fluid in a laminar region. Numerical studies were carried out in a two-dimensional square cavity in the presence of the sinusoidal roughness elements. The sinusoidal roughness elements were located on both the hot and cold walls with an amplitude of 0.1 and number of elements equal to 10. The presence of the sinusoidal roughness elements resulted in reduction of the average heat transfer. The maximum decrease in the average heat transfer was 23.33% at Ra number equal to 106. The formation of eddies or vortices in the wakes of the sinusoidal roughness elements, reduction in the volume of the fluid, and decrease in the effective distance between two isothermal walls may be the main factors affecting the fluid flow and the average heat transfer in the presence of the roughness in a square cavity.
NOTES
*Corresponding author.