A Particle Swarm Optimization to Minimize Makespan for a Four-Stage Multiprocessor Open Shop with Dynamic Job Release Time

Hui-Mei Wang¹, Fuh-Der Chou^2*

¹Department of Hotel Management, Vanung University, Taoyuan, Chinese Taipei.
²Department of Industrial Management, Chien Hsin University, Taoyuan, Chinese Taipei.

DOI: 10.4236/wjet.2015.33C012                

Abstract

This paper considers the scheduling problem observed in chip sorting operation of LED manufacturing, where each lot (job) with release time have four operations to be processed on a set of processing stages without pre-determined necessary route. Each stage has one and more identical sorting machines. The sorting machines scheduling problem can be treated as a four-stage multiprocessor open shop problem with dynamic job release, and the objective is minimizing the makespan in the paper. This problem is formulated into a mixed integer programming (MIP) model and empirically shows its computational intractability. Due to the computational intractability, a particle swarm optimization (PSO) algorithm is proposed. A series of computational experiments are conducted to evaluate the performance of the proposed PSO in comparison with exact solution on various small-size problem instances. The results show that the PSO algorithm could finds most optimal or better solutions in one second.

Keywords

Open Shop, Multiprocessor, Makespan, Particle Swarm Optimization

1. Introduction

LED manufacturing consists of hundreds of process steps, generally, these processes can be divided into two main phases: front-end and back-end. In Front-end phase is to produce LED wafer where the process is similar to semiconductor wafer fabrication, and back-end includes wafer polishing, epiwafer scribing, chip probing, chip sorting and finally each chip then go to assemble into different products such as lamp, SMD or other display equipment according to its application. This paper focuses on chip sorting operation which is performed in sorting machines. The purpose of the sorting machine is to separate diodes form the epiwafer and transport those to the corresponding bin frames according to identified grades for the next process of package [1] [2]. The sorting machine can classify at most 32 grades for each epiwafer, and a total of 128 grades is used to classify each chip. Therefore, each epiwafer have four operations to be processed on sorting machines without pre-specified obligatory route. Additionally, in real world, there is at least one sorting machine in each operation (or stage) and all lot (job) do not arrive for be processing in a time. The investigated sorting machine scheduling problem in LED manufacturing can be treated as a type of multiprocessor open shop scheduling problem with job release time and the objective to improve production efficiency, that is, to minimize the maximum of the completion times of all jobs, i.e., the minimization of the makespan, which, to the best of our knowledge, has not been studied by many researchers. The unique objective and constraints even increase complexity of the problem, which makes a complete mathematical model and an efficient solution necessary.

The multiprocessor open shop scheduling problem (MOSP) consists of n jobs with s operations to be processed on s processing stages in any sequence. Each stage has a number of parallel identical machines. Each operation of job j requires 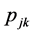for being processed on any of the parallel machines in one and only one stage k 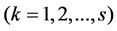without preemption. The MOSP problem is extended version of open shop problem. Some special cases of MOSP problem have been investigated by other researchers. For example, a special case of the MOSP is proportionate multiprocessor open shop scheduling problem (PMOSP) in which the processing time is not job-dependent, that is, each operation in k stage requires the same processing 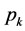time. The PMOSP is encountered in auto-repair and washing, maintenance workshops, final inspection operations and diagnostic test of hospital health care [3]. Matta [3] [4] is the first to address the PMOSP in the literature and she proposed two mixed integer programming models to solve the problem with the objective of minimizing the makespan. With the complexity of the problem, a genetic algorithm (GA) was also proposed to obtain efficient solutions in a reasonable time. Tamer [5] applied tabu search (TS) for the PMOSP with minimizing the makespan.

Another special case of MOSP is the open shop scheduling problem (OSSP) which has been attracted by many researchers and most of the published work considers the OSSP with the objective of minimizing the makespan. Brucker et al. [6] developed a branch-and-bound algorithm using disjunctive graph model for the OSSP problem with makespan objective, and then Gueret et al. [7] addressed improving technique for the branch-and- bound algorithm proposed by Brucker et al and examined it on benchmark problems of Taillard [8]. Liaw [9] developed a hybrid genetic algorithm (HGA) where TS algorithm is used for local improvement to solve OSSP with the objective of minimizing the makespan.

Unlike the open shop problem under certain objectives that has attracted considerable attention; MPOS problem has been very limited with only a few studies to date. Shiang et al. [1] is the first to model the LED sorting system as MPOS problem and applied Arena simulation model with five dispatching plans individually to solve it. Naderi et al. [10] constructed a mixed integer programming (MIP) model to solve MPOS problem with minimizing total completion time. They also proposed a memetic algorithm with simulated algorithm (SA) to obtain efficient algorithm in a reasonable time. According to the survey work of Ellur and Ramasamy [11], a variety of the open shop problem with different objective function has been considered in the literature, however, less interest to develop a particle swarm optimization (PSO) algorithm to solve MOSP problem is apparent in the literature when compared to other scheduling problems. Therefore, in this paper we formulate the LED sorting machine scheduling problem as a mixed integer programming model to specify the problem and to obtain optimal solutions as benchmarks, furthermore, we propose a PSO algorithm. To examine the performance of the proposed PSO, the solutions obtained by the PSO is compared with ones obtained by MIP model.

2. Mixed Integer Programming Model (MIP)

The LED sorting machine scheduling problem in this paper can be denoted by 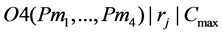in the standard classification [12]. Each job should be processed only once by one machine in each stage without pre-determined route. After the four stages being finished for job j, a completion time of job j is recorded as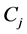. This paper attempts to find an optimal schedule to minimize the completion time when all jobs are finished, i.e.,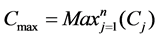. To obtain an optimal solution constructing a MIP model is traditional and intuitional methodology, and it is also nature way to specify explicitly and precisely the characteristics of problem.

2.1. Notation

n: number of jobs

s: number of stages

: Number of machines at each stage k,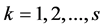

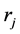: release time of job j,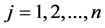

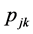: processing time of job j at stage k

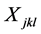: 1 if job j is processed at stage k before than stage l and 0 otherwise,;;

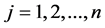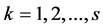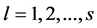
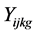: 1 if job i is processed before job j for machine g at stage k and 0 otherwise,;;;

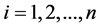: 1 if job j is processed on machine g at stage k and 0 otherwise,;;

: the completion time of job j

: the completion time of job j at stage k

: makespan

2.2. Model

Min

(1)

Subject to

(2)

; (3)

; (4)

; (5)

;;;; (6)

;;; (7)

;;; (8)

;;; (9)

;;; (10)

(11)

The objective (1) is to minimize the makespan. Constraints (2) specify that the precedence relationship between stages for processing job j. Constraints (3) ensure that each job scheduled only once to be processed by one machine at each stage. Constraints (4) are used to calculate the completion time for each j at stage k. Constraints (5) define that the completion time of job j. Constraints (6) specify that the precedence relationship between two stages (k and l) for processing job j and ensure that stage k is either preceded by stage l or succeed by stage l for processing job j. Constraints (7) specify that two jobs must have precedence relationship if the two jobs (i and j) are processed on the same machine for each stage, and ensure that job i must be either preceded by job j or succeeded by job j if the two jobs are processed on the same machine for each stage. Constraints (8) and (9) define the relationship of two jobs (i and j) being processing on the same machine at stage k and ensure that the completion time of job j has to be greater than or equal to the completion time of job i. Constraints (10) define that the completion times of two jobs (i and j) which are processed on the same machine at stage k. Constraints (11) specify that the makesapn.

3. Particle Swarm Optimization (PSO)

As a majority of combinational optimization problem like scheduling problems is difficult to obtain optimal solutions, some meta-heuristic algorithms such as simulated algorithm (SA), genetic algorithm (GA) and particle swarm optimization (PSO) are proposed for those tough problems. PSO was developed by Kennedy and Eberhart [13] for optimization of continuous non-linear functions, and then extended to solve discrete or combinational optimization problems including scheduling problems. Inspired by the motion of a flock of birds searching for food, the search process of PSO is a constructive cooperation between particles as opposed to survival of the fittest approach used in GAs.

However, similar to other evolutionary algorithms, PSO algorithm also starts with a population of initial solutions called particles. Each particle is located at position with its velocity. In the PSO, each particle is measured by the fitness value that defines the quality of solution. Furthermore, the position of each particle is adjusted to move toward a better feasible solution for the problem based on its own best movement experience and that of all other members until a stopping criterion is satisfied. The proposed PSO for the problem is addressed as follows.

Step 1: Generate initial particles randomly

Suppose there are n jobs to be scheduled through four stages without pre-deterministic sequence and each dimension is represented as a job in -Dimensional space where is equal to. Consequently, each particle i at iteration t is defined as

where represents the continuous position value of the ith particle with respect to the jth operation in tth iteration. In this representation, the rank order value is used to form an operation permutation. In this paper, the fifty initial particles are generated.

Step 2: Give an initial position and velocity

In this PSO, the initial position and velocity for each particle is randomly generated according to the two equations

, and

where, , , , and denotes a random number uniformly distributed in [0,1].

Step 3: Fitness of particles

Fitness value plays an important role to adjust the movement for each particle from the current position value to the next one at iteration t. In this study, the fitness value of a particle is defined by the makespan. For each given particle, we use a decode procedure to construct a complete schedule according to each particle from step 1 and obtain the fitness, i.e. to obtain makespan for each particle. The decode procedure includes three steps as follows:

Step 3.1 Generate a string with number between [0,1] randomly

Step 3.2 Apply rank order value (ROV) method to produce a list

Step 3.3 Use the following equations to generate an operation permutation for the list.

, ,

To explain the decode procedure to obtain makespan for each particle; an example is given as shown in Table 1 and Table 2. If (0.859, 0.600, 0.022, 0.393, 0.800, 0.326, 0.963, 0.984, 0.751, 0.149, 0.403, 0.065, 0.842, 0.097, 0.429, 0.138, 0.439, 0.602, 0.970, 0.339) of a string is generated randomly, and then (3, 12, 14, 16, 10, 6,

Table 1. The example with five jobs with four stages.

Table 2. The number of machine in each stage.

20, 4, 11, 15, 17, 2, 18, 9, 5, 13, 1, 7, 19, 8) of an list is obtained by rank order value (ROV). Finally, apply two above equations to generate a corresponding operation permutation, for example, the first value is equal to 3 in the list, we can obtain operation which indicates job 3 is assigned to stage 1. The complete operation permutation is {, }, and based on the operation permutation and non-delay concept, the 30 of makespan can be obtained.

Step 4: Particle movement

In the PSO, each particle is designed to move toward its own best position (pbest), and the best position of the whole swarm (gbest) by velocity updating mechanism. Several velocity equations have been developed in the

literature. This paper uses the standard formula where w is

the inertia weight used to control exploration and exploitation. A higher value of w prevents particles from getting trapped into local optimal. Meanwhile, a smaller value of w forces them to exploit under the same search area. Constants and are respectively called cognitive and social parameters, which determine whether particles prefer to move closer to the pbest or gbest positions, while and are uniform random numbers

between 0 and 1. Once the velocity of each particle is updated for iteration t, each particle’s new position is generated by, where is the position of the particle i at the previous iteration. In this paper, and are set to 2, and w is equal to 1.

Step 5: Stopping criterion

For a PSO, this paper use time limit to terminate the PSO procedure. When execution time of the proposed PSO is greater than or equal to 1 second, terminate the PSO and print out the final best schedule, otherwise go to Step 3.

4. Result

For testing performance of the proposed PSO, random test problem instance are generated. This test problem can be formally as follows: a set of n (n = 5, 10, 15, 20) jobs to be processed in a 4 stage multiprocessor open shop where the number of machines in each stage is generated are generated from a uniform distribution between 1 and 3. The processing time () are generated from the uniform distribution in the ranges [1,20], and the release time () from uniform distribution between 0 and 50. For each problem, 20 instances are generated, totally 80 instances are generated. IBM ILOG CPLEX Optimization Studio Version 12.5 is used to test the effectiveness of proposed MIP model, and PSO is coded in C++ gcc version 4.8.4 , all tests are conducted on a LINUX (Ubuntu 14.04LTS) with Intel Xeon E5-1630 3.7 GHz (12GB RAM).

Five independent replications of a PSO run for each test instance, and the best solution is obtained as the resulting performance measure values. For MIP model, all optimal solutions can be obtained within 3600 CPU time (in seconds) for the problems with five jobs, while for other problems the solutions are not sure for optimal solved within 3600 CPU time. Table 3 provides results for MIP and PSO. The columns under “Av. C_max” give the average C_max value over 20 instances. The other columns under “#best” denote the number of time each method finds the optimal or the best solutions. From Table 3, it is obvious that PSO and MIP are equivalent when comparing the average C_max values, however, PSO finds slightly better solutions for larger problems (n = 20), furthermore, the average CPU time consumed by MIP significantly increases incredibly as the problem size increases, it is expected that the solutions of the problems that are larger than 20 jobs could not be obtained in 3600 CPU times (in seconds).

5. Conclusion

The main contributions of this paper is the formulation of the LED sorting operations into a 4-stage multipro- cessor open shop problems with job release time and proposes the PSO algorithm. Based on the results of an

Table 3. The results obtained by MIP and PSO.

experiment, the proposed PSO has successfully obtain the optimal or best solutions for problems with up to 20 jobs in 1 second. The results demonstrate that the proposed PSO is outstanding, and additionally the PSO algorithm should be very promising for actual problems in the real world environment. To further examine the performance of the PSO, a valid and effective lower bound for the problem is needed for future research, additionally; developing different meta-heuristic algorithms is also an attractive research direction.

Acknowledgements

This paper was supported in part by the Ministry of Science and Technology, Taiwan, ROC, under the contract NSC 100-2221-E-231-007.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shiang, W.-J., Lin, Y.-H. and Rau, H. (2009) Application of Simulation to the Scheduling Problem for a Led Sorting System. Proceedings of the Eighth International Conference on Machine Learning and Cybernetics, Baoding, 2875-2879.
[2]	Wu, T., Li, B., Wang, L.-W. and Huang, Y. (2010) Study on Auto-Path Planning According to Grade Priority for Sorting Dies. Proceedings of the Ninth International Conference on Machine Learning and Cybernetics, Qingdao, 11-14 July 2010, 1590-1595. http://dx.doi.org/10.1109/icmlc.2010.5580803
[3]	Matta, M. (2004) An Empirical and Theoretical Study of Outpatient Scheduling Problems Employing Simulation and Genetic Algorithm Methodologies. Ph.D. Thesis, Duke University.
[4]	Matta, M.E. (2009) A Genetic Algorithm for the Proportionate Multiprocessor Open Shop. Computers & Operations Research, 36, 2601-2618. http://dx.doi.org/10.1016/j.cor.2008.11.009
[5]	Tamer, F.A., Mohamed, A.S. and Mohamed, A.A. (2014) A Tabu Search Approach for Proportionate Multiprocessor Open shop Scheduling. Computational Optimization and Applications, 58, 187-203. http://dx.doi.org/10.1007/s10589-013-9621-0
[6]	Brucker, P., Hurink, J., Jurisch, B. and Wostmann, B. (1997) A Branch and Bound Algorithm for the Open Shop Problem. Discrete Applied Mathematics, 76, 43-59. http://dx.doi.org/10.1016/S0166-218X(96)00116-3
[7]	Gueret, C., Jussien, N. and Prins, C. (2000) Using Intelligent Backtracking to Improve Branch-and-Bound Methods: An Application to Open-Shop Problems. European Journal of Operational Research, 127, 344-354. http://dx.doi.org/10.1016/S0377-2217(99)00488-9
[8]	Taillard, E. (1993) Benchmarks for Basic Scheduling Problems. European Journal of Operational Research, 64, 278- 285. http://dx.doi.org/10.1016/0377-2217(93)90182-M
[9]	Liaw, C.F. (2000) A Hybrid Genetic Algorithm for the Open Shop Scheduling Problem. European Journal of Operational Research, 124, 28-42. http://dx.doi.org/10.1016/S0377-2217(99)00168-X
[10]	Naderi, B., Fatemi, Ghomi, S.M.T., Aminnayeri, M. and Zandieh, M. (2011) Scheduling Open Shops with Parallel Machines to Minimize Total Completion Time. Journal of Computational and Applied Mathematics, 235, 1275-1287. http://dx.doi.org/10.1016/j.cam.2010.08.013
[11]	Ellur, A. and Ramasamy, P. (2015) Literature Review of Open Shop Scheduling Problems. Intelligent Information Management, 7, 33-52. http://dx.doi.org/10.4236/iim.2015.71004
[12]	Graham, R.L., Lawler, E.L., Lenstra, J.K. and Rinnooy Kan, A.H.G. (1979) Optimization and Approximation in Deterministic Sequencing and Scheduling—A Survey. Annals of Discrete Mathematics, 5, 287-326. http://dx.doi.org/10.1016/S0167-5060(08)70356-X
[13]	Kennedy, J. and Eberhart, R. (1995) Particle Swarm Optimization. Proceedings of the IEEE International Conference on Neural Networks, 4, 1942-1948. http://dx.doi.org/10.1109/ICNN.1995.488968