Increasing Road Traffic Throughput through Dynamic Traffic Accident Risk Mitigation ()
1. Introduction
With the advent of vehicular ad-hoc networks (VANETs), vehicles are able to share information and respond in real-time, leading to the ability for traffic management systems to be more dynamic, rapidly responding to current circumstances, and to be tailored to individual vehicles. This gives an opportunity to increase network throughput by more efficiently managing traffic flows. However, a key consideration is that such systems do not increase the accident risk to drivers, passengers and other road users.
To facilitate this, we introduce the notion of risk limits, whereby vehicles must maintain a sufficiently low probability of an incident occurring, and/or a sufficiently minor impact of such an incident in terms of injuries to people and damage to property. These risk limits would be dynamic and calculated in real-time based on the characteristics of each driver and vehicle as well as prevailing environmental conditions. Vehicles would then be able to behave in a way that optimises the utility of the road network―both in terms of the speed of individual vehicles and overall network throughput―as long as their risk does not increase above the set threshold.
In order to gain the most benefit from such a system, the differentiated nature of accident risk must be taken into account. Each driver, vehicle and situation has its own constellation of risk factors that may be rapidly changing and the range of risk levels experienced either by a single vehicle and driver over time or between different vehicles and drivers is significant. These differences can be exploited to obtain the maximum benefits to network utility while still maintaining an acceptable level of accident risk. Such a system would require the calculation of risk levels in real-time so as to determine appropriate vehicle behaviour.
An inter-vehicle communications network plays a key role in such a system, not only for co-ordinating the actions of different vehicles in an environment of differentiated behaviour but also as a means of conveying information about risk. Surrounding vehicles themselves constitute a source of risk and thus must communicate their own characteristics in order for vehicles to be able to make an accurate estimate of their current risk level.
In this paper, we propose a framework for managing risk levels with the aim of maximising the road network throughput. We show through an experimental study that it is possible to achieve both lowered accident levels and increased throughput simultaneously by exploiting the variation in risk between situations, dynamically striking a balance between risk and utilisation.
2. Determining Risk
The first step in maintaining a risk limit is to be able to determine the current level of risk. Risk as it relates to traffic accidents consists of four aspects: exposure, crash probability, injury probability and injury outcome [1] . Exposure refers to the amount of use of the system by a user or class of users, i.e. the amount of time spent or distance travelled on the road. Crash probability is the likelihood of being involved in an accident, given a particular exposure. Injury probability is the likelihood of sustaining an injury when involved in an accident and injury outcome is the eventual result of this injury.
Since we are interested in balancing accident risk with road system utility, we will concern ourselves primarily with crash probability and, to a lesser extent, injury probability, as these two aspects of risk―and of mitigating risk―have the most influence on utility. The other two elements of risk are beyond the scope of this work. Measures to affect exposure are typically too long-term to be relevant to research focusing on dynamic traffic management through the use of VANETs―their effects will persist and be stable over long periods of time rather than varying with the traffic situation, and cannot be influenced by individual vehicles or drivers as they travel. Injury outcome is largely a problem of logistics, economics and medical science and thus the benefits of a VANET are also limited or non-existent for this cause. Hence for this work, we consider risk primarily in terms of crash probability, as this is the aspect of risk that is most amenable to influence from a VANET-based traffic management system. In future, it would also be desirable to extend this model to include injury probability and this is discussed further in Section 8. However, as an initial step in developing a dynamic traffic management model, we will here only consider crash probability.
In order to come to an overall measure of risk, it is first necessary to determine the levels of the contributing risk factors. These factors can be broken up into three categories: human factors relating to the driver of the vehicle, factors relating to the vehicle itself, and environmental factors which relate to the current situation of the driver and vehicle such as weather, lighting, type of road, nearby hazards, and so on. This breakdown of risk factors can be seen in the first row of the Haddon matrix [2] [3] .
Although there have been many studies detailing various risk factors and their effects on accident rate, the current literature does not provide the knowledge necessary for devising a general model of risk such as that a particular driver is more accident prone or that a particular environmental hazard increases accident risk. To incorporate risk factors into a model, the need arises to determine how the vehicle moves at each timestep. For vehicular factors, this is often straightforward as we can calculate the effects of characteristics such as maximum deceleration or mass. This is also true for some environmental factors―typically those that have direct, physical effects on the vehicle. Factors relating to the driver of the vehicle, however, present significant challenges.
Human factors account for a large number of traffic accidents (percentages found vary between 65% and 75%) [4] -[6] , however these are also often the most difficult factors to model. For some temporary human risk factors, such as driver fatigue [7] and potential distractions such as mobile phone use [8] , technological advances have enabled closer monitoring of the driver in real time, which leads to a more accurate measure of these factors that does not require the active participation of the driver. When dealing with longer-term factors which may vary only over the course of months or years, however, those human factors which are relatively simple to model are also the ones least useful in determining risk. In [9] , the authors found that vehicle control skills had no correlation to accident risk. This is supported by findings that professional race drivers, a highly skilled subset of the driving population, have a higher accident involvement than other drivers [10] . Instead, it is factors relating to perception and cognition that are the best determinants of accident risk. Hazard perception [9] [11] , field dependence as measured by tests such as the embedded figures test and the rod and frame test [4] [12] -[14] , visual impairments [15] , selective attention skill [4] [14] [16] and drivers’ awareness of their own risk [4] [17] [18] have all been shown to predict accident risk.
Many of these factors have the problem that they are difficult, time-consuming or expensive to measure, often requiring extensive tests conducted by specialists. Even once measured, modelling them is a challenging task. Some attempts have been made to provide models of drivers’ perception and cognition [19] [20] and their emotions and personality [21] [22] , however these models are much more complex and difficult to implement than purely physical models of vehicle dynamics such as those proposed by [23] and [24] (which is the model used as the basis for Paramics, the simulation engine we used to conduct this research).
While these problems are substantial, it is still possible to obtain a coarse grained estimate of the risk value by using only one or a few factors―preferably those with the biggest contribution to accident risk, although the possible factors to use also depends on the available data. Even an incomplete risk estimate can give a measure of the difference in risk between different vehicles, drivers and environments and thus can be used as a means to inform changes in vehicle behaviour for the purposes of risk mitigation. Furthermore, as risk models requiring this information are developed, this gives a motivation for the research community to obtain the needed data about individual risk factors in order to improve the exactness of the risk model.
3. Risk Model
We propose a model in which information about the risk factors pertinent to a vehicle is combined to give a risk value. This is done by calculating a relative value for each factor; for instance, a factor which increases risk by 50% will have a value of 1.5, a factor which causes no change in risk will have a value of 1.0 and a factor which causes a 50% reduction in risk will have a value of 0.5. The individual values for each factor are averaged together to give the overall risk value for a vehicle. Note that since individual factors have different values, this means that the aggregate values for each of the three types of factors are not necessarily equal. This risk value can change rapidly as environmental conditions change and as other vehicles enter and leave the nearby area. A vehicle’s risk value can then be compared to the desired risk limit. If the current risk value is too high, the vehicle needs to undertake risk-mitigating behaviours to bring its current risk level down under a predefined limit. If the risk value is already below the limit, the vehicle has some scope to engage in utility-increasing behaviours. These behaviours will in general increase the vehicle’s current risk and should never cause the vehicle to exceed the risk limit. A diagram of the model’s structure is shown in Figure 1.
Risk-mitigating behaviours are any behaviours that reduce a vehicle’s current risk level. These may include reducing speed, increasing headway, changing lanes, or changing route. Utility-increasing behaviours are those which improve the utility of the road system, comprising the speed at which vehicles can travel and the overall throughput of the system. These behaviours may include increasing speed, decreasing headway and, again, changing lanes or route.
This model is designed to be modular so that as risk factors are increasingly able to be understood, measured and modelled, they can be added to the model with mininal alteration to the overall algorithm. Similarly, further risk-mitigating and utility-increasing behaviours can be added and a given vehicle can choose a combination of behaviours from the known set, appropriate to its current situation.
In order to implement this model, the following components are required. First, an understanding of at least some of the risk factors affecting a vehicle and a measure of how much each of these affects accident risk.
Second, an understanding of the effects of some risk-mitigating and utility-increasing behaviours for vehicles to use and finally, a system to tie these two together: to calculate risk dynamically in real-time and modify vehicles’ behaviour accordingly.
In the remainder of the paper we detail how we have obtained the initial risk levels and carried out an experimental study to investigate the feasibility of the approach. In Section 4, we detail the process of calculating risk values from real-world traffic accident data; Section 5 covers our experimental setup and Section 6 describes our investigation of the effects of specific behaviours on risk levels and Section 7 presents the results. Section 8 discusses future directions for this work and Section 9 concludes this paper.
4. Calculating Risk from the NSW CrashLink Database
The NSW Roads and Traffic Authority collects data from traffic accidents on state roads. All accidents which result in death or injury or in at least one vehicle being towed away are recorded in the CrashLink database. A section of this database was used for analysing the feasibility of calculating risk values and a method for doing so. The data used was from the F3 (Sydney to Newcastle) Freeway for the years 2004 to 2008 inclusive.
4.1. Selecting Risk Factors for Analysis
Although there are a large number of parameters contained in the crash database, not all of them are suitable for calculating risk values for the purposes of modifying vehicle behaviour. While the database records the number of incidents for any given combination of factors, what is not known is the number of vehicles or drivers who share these characteristics and did not crash, i.e. the exposure for any given risk factor. This means that it is difficult to reliably distinguish between an increased number of crashes due to a larger prevalence of a given risk factor in the general population, and an increased number of crashes due to increased accident-proneness correlating to that risk factor.
In order to gain an estimate of the proportion of the general population of drivers and vehicles that share a particular risk factor, we use induced exposure [25] [26] . In this method, an estimate is made of the total proportion of vehicles on the road matching a particular factor by dividing vehicles involved in accidents into those that are considered at-fault, or at least partly responsible for the accident, and those that are not. For instance, in a single-vehicle accident, that one vehicle is considered entirely at fault, while in a multi-vehicle accident, the first two vehicles to collide may be considered responsible.
The CrashLink database contains a field for each vehicle specifying whether that vehicle was the key traffic unit in the accident in which it was involved, i.e. whether it was the primary at-fault vehicle for that accident. We use this field to differentiate between vehicles that were at fault and those that were not. We then compare the proportion of at-fault vehicles or drivers to the proportion of not-at-fault vehicles or drivers to get a measure of the risk of accident involvement associated with a given risk factor or set of factors. We chose a set of seven risk factors to analyse in this way: driver age, driver gender, vehicle make, number of occupants of the vehicle, vehicle speed at time of crash, vehicle type and year of manufacture of the vehicle. Because induced exposure relies on determining the proportion of not-at-fault vehicles or drivers that possess a particular risk factor, it is not possible to use this methodology to analyse environmental risk factors. Thus our set of factors all relate to either vehicles or drivers.
4.2. Calculating Risk Values
To calculate the risk value for a given set of factors, we first need to calculate the proportion of the at-fault vehicles which have that factor using the key traffic unit field. For instance, in the crash database, 1604 of the key traffic unit drivers are listed as male, out of 2212 key traffic unit drivers total, giving us an at-fault population proportion of 1604/2212 = 0.725. Note that when calculating proportions, individual records are only included if all risk factors being considered are complete―if any fields are missing, those vehicles or drivers are excluded.
Following on, we estimate the proportion of not-at-fault vehicles or drivers having that risk factor. To continue the previous example, 1015 out of 1369 not-at-fault drivers were listed as male, giving us a proportion of 1015/1369 = 0.741 of the not-at-fault population. Finally, we take the ratio of the crash population proportion to the not-at-fault population proportion, giving us a risk value of 0.725/0.741 = 0.98. This method can be extended to any number of risk factors by selecting the proportions of the at-fault and not-at-fault populations that have all the risk factors in question.
Figures 2-4 give risk value calculations for each risk factor. For two factors, gender and number of occupants of the vehicle, we have also conducted the same analysis restricted to young drivers only. These factors have often been raised in the debate about licensing rules for young drivers and thus analysis specific to young drivers on these factors may prove of interest.
Calculations of this sort may take significant time relative to the necessary response time of a traffic management application, particularly for combinations of many factors. However, these calculations would not need to be performed every time a risk value was needed, as results could be pre-computed and stored for fast look-up. This means that providing individual, differentiated risk estimates, a requirement of our risk limit traffic management model, is viable.
Additionally, as VANETs see more widespread use, we can expect more and better quality data to become available for calculating risk values. In particular, VANETs promise an unprecendented opportunity to gather complete and accurate exposure data for traffic accident risk, as vehicles will be constantly transmitting their state and characteristics over the network. Collection and management of this data brings its own set of challenges, in particular with regards to the sheer scale of data to be collected and management of road users’ privacy. Nonetheless, risk estimates should become more accurate and incorporate more risk factors in the future.
5. Simulation Environment
Once risk values have been determined, they can be used to inform vehicle behaviour in order to maintain a given risk limit. To investigate a means of doing this, simulations were conducted using the Quadstone Paramics Microsimulator (version 6.7.2).
5.1. Simulating Accidents
By default, Paramics does not have any mechanism for simulating traffic accidents. Hence, in order to study accident rate, it is first necessary to model accidents in the simulation. Although accidents are not themselves modelled in Paramics, the car-following model used extends to situations in which vehicles are separated by
![]()
Figure 2. (a) Risk values by gender; (b) Risk values by gender for young drivers (age less than 25 years); (c) Risk values by age.
![]()
Figure 3. (a) Risk values by vehicle make; (b) Risk values by vehicle type; (c) Risk values by number of occupants of the vehicle.
![]()
Figure 4. (a) Risk values by number of occupants of the vehicle for young drivers (age less than 25 years); (b) Risk values by vehicle speed at time of crash; (c) Risk values by year of manufacture of vehicle.
small distances―well below required stopping distances―and where acceleration and deceleration reach the physical constraints of the vehicle [27] . As such, it was possible to model traffic accidents in Paramics.
This is done by modelling dangerous behaviours that have the potential to lead to accidents. Vehicles in Paramics will by default never perform dangerous actions such as sudden braking, running a red light, changing lanes without checking for a gap etc. In reality however, most accidents are caused by such cases of human error [5] [6] . Two dangerous actions―sudden braking and lane changing without gap checking―have been implemented to act as potential causes of accidents. These actions are performed on a stochastic basis and braking can be of any magnitude up to the vehicle’s maximum deceleration.
The results of these actions are then left up to the simulation engine to play out, so that for many dangerous actions, no accident occurs as there are no other vehicles nearby or drivers are able to avoid colliding with the vehicle performing the dangerous action. Once vehicles have collided, they are removed from the simulation as we do not wish to model the effects of incidents but rather the frequency of accidents occurring, so it is important that all vehicles travel under the same conditions, i.e. without any incident-related congestion or road closures.
5.2. Road Network and Simulation Parameters
The road network used for the following experiments was a test network developed for this purpose. It consists of two links (forming one bi-directional road), each with four lanes, and two zones. Each zone acts as an origin for one of the links and a destination for the other. Vehicles are evenly distributed between the two links. Each simulation runs for two hours (simulation time) including warmup. During this time vehicles are constantly released onto each link as fast as possible, i.e. vehicles will not exceed their maximum speed and will maintain headway according to the Paramics car-following model from the time they are released onto the link. A diagram of the road network can be seen in Figure 5. Each simulation was run 10 times for each datapoint, with the exception of the control simulation, which had 100 runs.
6. Vehicle Behaviour and Accident Rate
In order to change the accident rate by modifying vehicle behaviour, it is vital to first understand how particular behaviours affect the accident rate. To do this, experiments were conducted in which first speed and then headway were varied and the accident rate observed. These experiments were carried out using the test network described in Section 5.2 with a simulation duration of 2 hours for each datapoint in our graphs.
Each vehicle in Paramics attempts to drive at a maximum speed for the link it is currently on. Most of the time, the maximum speed matches the speed limit for the link, however under some circumstances this may be different for particular vehicle types or links, e.g. a heavy vehicle which has its speed limit set lower than that of the link it is on, or for vehicles with a high driver aggressiveness factor, which may seek to exceed the speed limit. However, using the programming API, it is possible to manually set the maximum speed for each vehicle. This effectively represents the target speed for that vehicle, i.e. the speed it will travel at when not constrained by other, slower vehicles.
In the first experiment, the maximum speed was varied by a factor ranging from 0.1 in the first set of simulations to 3.5 in the last set. This was multiplied by the default maximum speed for that vehicle. The accident rate was then observed (see Figure 6(a)). A line of best fit was calculated to give an approximation of the relationship between speed and accident rate in Paramics and is given by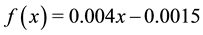 .
.
Since here we are varying maximum speed―i.e. a vehicle’s target speed―not the actual speed vehicles travel at, the speed vehicles will travel at is affected not only by this parameter but also constraints due to other traffic. This results in a relatively complex, non-linear relationship with accident rate. However, for our purposes, it is not necessary to fully investigate this function but we instead choose to take a simple linear approximation
as an initial estimate. As will be seen in later sections, this is sufficient to achieve improvements in road system efficiency whilst maintaining the accident rate.
However, the more accurately vehicle behaviour and its relationship with accident rate can be modelled, the better the results that can be expected. As such, an important direction for future work in this area is to improve the model of vehicle behaviour. This will be discussed further in Section 8.
The second experiment involved varying the headway factor of the vehicles. The default headway in Paramics is 1 second, however, each vehicle also has a headway factor, primarily based on the vehicle type, which is multiplied by the default headway in order to give a target headway for that vehicle. To test the effect of headway on accident rate, an additional headway factor, ranging from 0.1 in the first set of simulations to 3.5 in the last set, was multiplied by the target headway of each vehicle. The resulting accident rate function is shown in Figure 6(b). A decaying exponential function was fitted to this curve, with the resulting function of
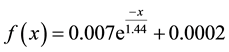 .
.
![]()
Figure 6. (a) Max speed factor vs. accident rate; (b) Headway factor vs. accident rate.
7. Modifying Vehicle Behaviour
7.1. Determining Risk
The first step in adjusting vehicle behaviour to compensate for risk levels is to determine the risk value for each vehicle. However, this presents significant difficulties, especially in modelling risk factors, as discussed in Section 2, and so only the vehicle type is included in our initial experiments with the added benefit that it is already modelled in some detail in Paramics. Differences between vehicle types include mass, height and width, and maximum deceleration. There were five different vehicles types in the simulation: car, Large Goods Vehicle (LGV), Other Goods Vehicle (OGV) types 1 and 2 (with differing dimensions), and coach.
To calculate the risk value for each type, a control simulation was run in which vehicle behaviour was not modified except for introducing dangerous actions as described in Section 5.1. The control simulation went for 100 runs, each of which were 2 hrs (simulation time) in length, on the network described in Section 5.2. From this simulation, the accident rate for all vehicles was calculated by the formula
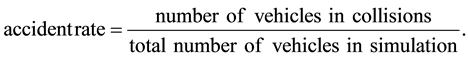
Accident rates were then calculated similarly for each vehicle type, giving a proportion of the vehicles of that type that were involved in collisions. The risk for a given vehicle type is given by
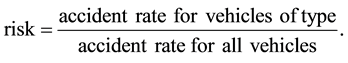
Risk values for each vehicle type are given in Table 1.
Having determined its own risk value, each vehicle then communicates this value to surrounding vehicles. For this initial study, we have not used a full wireless networking model, but instead have communicated these values between vehicles using the Paramics API. Vehicles primarily use their own risk value and that received from the vehicle in front (as this is most relevant for determining appropriate headway) in order to decide their behaviour.
7.2. Adjusting Behaviour
Vehicle behaviour was adjusted according to a risk threshold, which represents the desired risk limit. Vehicles with a risk value higher than the risk threshold were required to adjust their behaviour so that they were driven more safely, thereby bringing them down to the threshold. Vehicles with a risk value lower than the threshold were allowed to be driven at higher risk, e.g. faster, in order to improve the utility, i.e. average vehicle speed and overall throughput of the network.
Three different vehicle behaviours were affected in this way: maximum speed, target headway and lane changing. Maximum speed refers to the speed the vehicle prefers to travel on the link. A vehicle will accelerate until it reaches its maximum speed, unless it is constrained by the speed of surrounding vehicles or by other conditions such as an approaching intersection. Since the simulation network did not contain any intersections, the only constraints on a vehicle’s speed were its maximum speed for the link and the speeds of surrounding vehicles.
![]()
Table 1. Risk values by vehicle type.
Target headway is the time a vehicle aims to keep between itself and a preceeding vehicle, as opposed to headway which is the actual instantaneous time between the two vehicles. A vehicle will accelerate to get closer to the lead vehicle if its current headway is greater than the target headway, and decelerate to get further away from the lead vehicle if its current headway is less than the target headway. The acceleration or deceleration applied also depends on the relative speeds of the two vehicles. Paramics breaks the headway/velocity-difference space into five regions, each of which have different behaviours. Further details on this can be found in the Paramics Technical Report [27] .
Lane changing was modified in the following way. If the vehicle’s risk value was below the threshold, the vehicle would attempt to change into the adjacent lane which would allow it to go the fastest. If the vehicle’s risk value was above the threshold, it would change into the lane which was the least risky―i.e. the lane in which surrounding vehicles had the lowest risk values, or a lane with no nearby vehicles if there was one. In cases where a choice was not clear, vehicles would choose the lane closest to the kerb.
The exact functions for modifying speed and headway are derived from the curves of best fit shown in Figure 6(a) and Figure 6(b). The headway function is
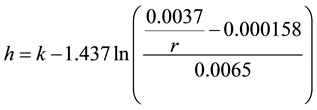
where h is headway factor, which is multiplied by the vehicle’s default headway factor given by the Paramics simulation engine, k is an adjustment constant of 0.2, so that headway factors are slightly over-estimated, giving an overall decrease in risk at the cost of some utility, and r is given by
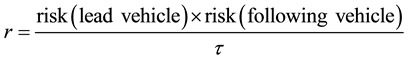
where  is the risk threshold.
is the risk threshold.
The function for maximum speed is
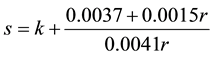
where s is the maximum speed factor, which is multiplied by the default maximum speed given by the Paramics simulation engine, k is an adjustment constant of −0.2, so that maximum speed is slightly under-estimated, and r is given by
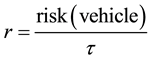
where ![]() is the risk threshold.
is the risk threshold.
The adjustment constants k are used to account for inaccuracies in the model. We wish to improve road system utility whilst maintaining the accident rate. As such, it is more important to keep the accident rate at or below control levels than to achieve greater gains in efficiency. We therefore take a slightly conservative estimate for headway and maximum speed. As the accuracy of the vehicle behaviour model improves, it should be possible to reduce or even eliminate these constants without violating the constraint of keeping below the risk limit.
7.3. Results
Simulations were run with risk thresholds ranging from 0.1 to 3.5, with 10 simulations runs for each value. The results are shown in Figures 7(a)-(c), plotted with 95% confidence intervals.
Table 2 gives the values of accident rate, average vehicle speed and arrival rate for risk thresholds between 0.7 and 1.5, as well as percentage differences from the control simulation. Instances where the results were improved over the control simulation are in bold.
We can see that for risk thresholds between 1.1 and 1.4 inclusive, we get an improvement in all three measures. For risk thresholds outside of this region, one or more of the measures is improved, however this comes at a
![]()
Figure 7. (a) Risk threshold vs accident rate; (b) Average vehicle speed vs. risk threshold; (c) Arrival rate vs. risk threshold.
price―we may have decreased accident risk but average vehicle speed and arrival rate are also below the control level, or the utility (throughput and speed) of the network may be improved, but the accident rate is also increased above the control. Accident rates in this region range from 91.52% to 92.64% of the control rate, while average speed is improved by between 21.98% and 74.61% of the control. The arrival rate shows improvements from 5.83% to 15.61%.
8. Future Work
While our results indicate that the risk limit model is a viable and effective means of traffic management, with benefits to road system utility, our work currently has a number of limitations and areas for possbile improvement. We will discuss some of these in the following sections.
8.1. Accident Risk Data
As discussed in Section 2, there is a scarcity of data on accident risk in an appropriate form to be used in the risk limit system. Since the model relies on differentiating between drivers’ and vehicles’ risk levels in order to leverage these differences for utility gains, the more risk factors that can be used in calculating the risk level, the better. In addition, improving the accuracy of the risk estimate allows the system to operate more efficiently while still remaining safe. To these ends, a useful direction for future work would be to gather and analyse more data on accident risk, particularly on the exposure for various risk factors in order to compare this to accident rates.
More―and more accurate―data on the effects of various risk factors may also lead to improvements in calculating the overall risk level based on the levels of the various factors present. Many risk factors are likely to interact and while we have been able to test the system in a simulation environment where full information about the effects of each factor as well as combinations of factors is avaialble, this is not so straightforward in the real world and requires further work as more and more factors are added to the system.
8.2. Vehicle Behaviours
A key way of expanding the risk limit system is to add more risk-mitigating and utility-increasing behaviours to it and it has been designed to allow for this kind of modular extension. Thus far we have addressed speed, headway, and lane choice as possible behaviours for vehicles to take. However there are many more behaviours that can affect a vehicle’s risk and/or utility. These might include route choice, choosing to drive at a different time of day, when to overtake, and gap acceptance when changing lanes or negotiating intersections.
Additionally, there is room for improvement in the existing model of vehicle behaviour, particularly in the model of vehicle speed. In this work, we have used a relatively crude linear approximation of the relationship between maximum vehicle speed an accident rate. The maximum speed parameter was chosen in part because it is easily accessible using the Paramics API, whereas modifying vehicles’ actual speed was considerably more difficult to implement. However, in a real-world implementation, actual vehicle speed―rather than maximum speed―may be a more useful behaviour to employ in a traffic management system of this kind.
Vehicle speed is one of the most significant and well-studied factors in accident risk and is frequently cited as a contributing factor in accident reports. The probability of a crash involving an injury has been found to be proportional to the square of the speed, while the probabilities of a serious or fatal crash are proportional to the cube and fourth power of speed respectively [28] [29] . In future refinements of the vehicle behaviour model, it may be more fruitful to investigate using these models rather than improving the model of maximum speed as a risk-mitigating behaviour.
8.3. Crash Severity
One aspect of accident risk that we have not yet addressed sufficiently is crash severity; we have instead focused on accident rates in this work. However, crash severity is also an important consideration as not all accidents are equal in outcome. Currently, a minor accident at low speed resulting in property damage only is given the same weight as a high-speed accident resulting in severe injury or death. In future work, the potential outcome of a crash in terms of harm to vehicle occupants and other road users should be incorporated into the risk calculation to avoid this.
One means of doing this would be to adjust the risk level according to indicators that an accident, should it occur, would result in severe injury or death. Since accident severity depends heavily on factors such as speed at impact, vehicle mass, and the presence of safety features designed to lessen the force on occupants at impact, it may be possible to determine the approximate severity of potential accidents based on the characteristics and state of the current vehicle and the vehicles surrounding it. The risk level could then be modified accordingly so that the risk limit can be achieved by affecting either accident probability, accident severity, or both.
9. Conclusions
In Section 4, we have shown how we can calculate the risk value for a given vehicle, driver and situation’s constellation of risk factors given raw data. We can pre-calculate risk values for combinations of factors to gain information about the interactions between factors. This can require significant computation time; however, it is only necessary to do once. The relevant data could then be stored on an on-board computer in each vehicle, or could be accessed via the network (or some combination of these). Combined with inter-vehicle communications, it is then possible for each vehicle to have up-to-date information on its own risk level and those of the vehicles around it.
Section 7 illustrates how such information can be used to modify vehicle behaviour―in particular speed, headway and lane-changing―at a fine-grained level in real-time. This allows us to take advantage of risk variation between vehicles to improve both safety and utility simultaneously. Even in our initial experiments we are able to make significant improvements to road utilisation while maintaining the accident risk at the control level. Given that a more complete risk model could be reasonably expected to make possible even higher gains, it is clear that the methodology of capitalising on the dynamic risk levels is promising for future safe and highly effective road networks. This is an initial study using only a simple test network and one risk factor (vehicle type) but this method can readily be expanded to apply to other networks and to incorporate more risk factors, once these are added to the simulation model.