1. Introduction
We use the standard notation. By an edge we mean an unoriented pair of vertices, and by an arc we mean an oriented pair of vertices. For a given graph G, 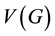 and
and 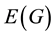 denote the set of its vertices and the set of its edges, respectively. For a digraph G, we write
denote the set of its vertices and the set of its edges, respectively. For a digraph G, we write 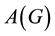 for the set of its arcs. By an oriented graph we mean such a digraph that if
for the set of its arcs. By an oriented graph we mean such a digraph that if 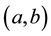 is an arc, then
is an arc, then 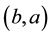 is not. All graphs and digraphs in this paper are finite.
is not. All graphs and digraphs in this paper are finite.
2. Motivation
Orientation of a graph G is called transitive if for every ,
, 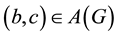 , also
, also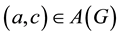 . This concept was studied by many authors in numerous papers, see the survey [1] for example. The concept of transitive orientation was generalized in several ways in [2] and [3] , [4] and [5] , and other papers.
. This concept was studied by many authors in numerous papers, see the survey [1] for example. The concept of transitive orientation was generalized in several ways in [2] and [3] , [4] and [5] , and other papers.
A digraph is called k-transitive if every directed path of the length k has a shortcut joining the beginning and the end of this path. In other words, if 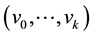 is a path in the digraph G, then
is a path in the digraph G, then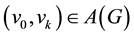 .
.
Note that our term “k-transitive” coresponds to “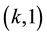 -transitive” in [2] and [3] .
-transitive” in [2] and [3] .
A k-transitive closure of an oriented graph 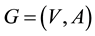 is an oriented graph
is an oriented graph 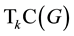 such that
such that
(1) 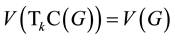
(2) 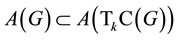
(3) 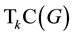 is k-transitive.
is k-transitive.
(4) it has the minimal (by inclusion) set of arcs among all graphs with the above stated properties.
Observe that there are oriented graphs for which the k-transitive closure does not exist. For example in a cyclically oriented cycle ![]() it is not possible to add arcs to fulfill the condition (3).
it is not possible to add arcs to fulfill the condition (3).
If the k-transitive closure does exist for some oriented graph, it is unique.
Note that this definition is a partial answer to the point (4) in ([2] , p. 41).
The aim of this paper is to describe k-transitive closures of directed paths.
3. Structure of the k-Transitive Closure of the Directed Path
Instead of ![]() we write
we write ![]() to denote the k-transitive closure of an oriented path on n vertices. We label the vertices by natural numbers
to denote the k-transitive closure of an oriented path on n vertices. We label the vertices by natural numbers ![]() and assume that
and assume that ![]() for
for![]() .
.
Although the graph ![]() is oriented, some of the properties will be stated for simple graphs obtained by “forgetting” the orientation. We belive that it is clear from the context, but to be precise, for the unoriented case we write
is oriented, some of the properties will be stated for simple graphs obtained by “forgetting” the orientation. We belive that it is clear from the context, but to be precise, for the unoriented case we write![]() .
.
In this paper by a degree sequence of a graph ![]() we mean a sequence
we mean a sequence![]() . (In/out) degree sequence of a graph
. (In/out) degree sequence of a graph ![]() is defined in a similiar way.
is defined in a similiar way.
Observe that ![]() is just the complete graph
is just the complete graph![]() , and
, and ![]() is the tournament on n vertices.
is the tournament on n vertices.
The starting point in a construction of the k-transitive closure of the path ![]() is to add arcs
is to add arcs![]() . Then we add arcs
. Then we add arcs![]() , at the next stage arcs
, at the next stage arcs![]() , and so on. This construction shows that for every
, and so on. This construction shows that for every![]() ,
, ![]() is well defined.
is well defined.
The key observations are:
3.1 Fact. Adding one vertex to the path adds only arcs ending in this new vertex. In other words, ![]() is an induced subgraph of
is an induced subgraph of![]() . □
. □
3.2 Fact. In the graph![]() ,
, ![]() iff
iff ![]() for some
for some![]() .
.
Proof. It follows directly from the construction described above that
![]()
To show the other inclusion we use the induction on n. First observe that for ![]() all arcs are of the form
all arcs are of the form![]() . Assume that all arcs in
. Assume that all arcs in ![]() have the length
have the length ![]() for some
for some![]() . To obtain a k-shortcut in
. To obtain a k-shortcut in ![]() we need k arcs, each of them of length
we need k arcs, each of them of length![]() ,
,![]() . So
. So
![]() . □
. □
In Figure 1 we present the graph ![]() as an example.
as an example.
4. Some Properties
From the observations mentioned above, we conclude several properties of graphs ![]() and
and![]() .
.
4.1 Fact. For![]() ,
,![]() . So for
. So for![]() , the graph
, the graph ![]() is just the path
is just the path![]() . □
. □
We can observe the following block structure in indegree/outdegree sequences of graphs![]() :
:
![]()
Figure 1. The graph![]() . All arcs ending in the last vertex are drawn with thick lines.
. All arcs ending in the last vertex are drawn with thick lines.
4.2 Theorem. Let ![]() for some
for some ![]() and
and![]() . In the oriented graph
. In the oriented graph ![]() the indegree sequence is built from uniform “blocks” of length
the indegree sequence is built from uniform “blocks” of length ![]() and has the form
and has the form
![]()
Similarly, the outdegree sequence is built from uniform “blocks” of length ![]() and has the form
and has the form
![]()
Proof. The proof follows from Facts 3.2 and 3.1. We prove the part concerning the indegree sequence. First note that the indegree of the first vertex is 0. For the next ![]() vertices there is no arcs ending in them other
vertices there is no arcs ending in them other
than the arcs in the initial path, so their indegree is 1. First vertex of indegree 2 is the ![]() -th vertex. First vertex of indegree 3 is the 2k-th vertex, and first vertex of indegree j is the
-th vertex. First vertex of indegree 3 is the 2k-th vertex, and first vertex of indegree j is the ![]() -th vertex.
-th vertex.
The proof for the outdegree sequence is similiar; we just start from the last vertex. □
4.3 Corollary. The graph ![]() is
is ![]() -regular for every
-regular for every![]() .
.
Proof. This is a consequence of Theorem 4.2; just observe that summing up the indegree and outdegree sequences gives the constant sequence![]() . □
. □
4.4 Corollary. For every![]() , and for every
, and for every![]() , all vertices of the graph
, all vertices of the graph
![]() has degree
has degree ![]() or
or![]() . Morover, if we put
. Morover, if we put ![]() and
and![]() , the degree sequence is built from “blocks” of the form
, the degree sequence is built from “blocks” of the form
![]()
repeated to get the sequence of the length![]() . Note that the last “block” has the length
. Note that the last “block” has the length![]() .
.
Proof. This is another consequence of Theorem 4.2. □
4.5 Corollary. For every![]() , and for every
, and for every![]() , in the graph
, in the graph ![]() there are
there are ![]() vertices of degree
vertices of degree ![]() and
and ![]() vertices of degree
vertices of degree![]() . □
. □
As an example, below are the degree sequences for 5-transitive closures of the paths on 10, 11, 12, 13 and 14 vertices:
• for![]() :
:![]() ;
;![]() ,
, ![]() and
and![]() , by Corollary 4.3 this graph is 2 + 1 = 3 regular;
, by Corollary 4.3 this graph is 2 + 1 = 3 regular;
• for![]() :
:![]() ;
;![]() ,
, ![]() and
and![]() , by Corollary 4.4 this sequence is built from repeated blocks
, by Corollary 4.4 this sequence is built from repeated blocks![]() ;
;
• for![]() :
:![]() ;
;![]() ,
, ![]() and
and![]() , by Corollary 4.4 this sequence is built from repeated blocks
, by Corollary 4.4 this sequence is built from repeated blocks![]() ;
;
• for![]() :
:![]() ;
;![]() ,
, ![]() and
and![]() , by Corollary 4.4 this sequence is built from repeated blocks
, by Corollary 4.4 this sequence is built from repeated blocks![]() ;
;
• for![]() :
:![]() ;
;![]() ,
, ![]() and
and![]() , by Corollary 4.3 this graph is 3 + 1 = 4 regular.
, by Corollary 4.3 this graph is 3 + 1 = 4 regular.
Recall that by degree of a vertex v in a digraph we mean a pair![]() .
.
For oriented graphs ![]() we can observe the following:
we can observe the following:
4.6 Corollary. Every constant subsequence in the degree sequence of the non regular graph ![]() is also the constant subsequence in the degree sequence of the oriented graph
is also the constant subsequence in the degree sequence of the oriented graph![]() . □
. □
For example, the degree sequence for ![]() is
is![]() , and the degree sequence for
, and the degree sequence for ![]() is
is![]() .
.
Recall that an oriented graph G is irregular if for every two vertices![]() ,
, ![]() , their degrees are different.
, their degrees are different.
Straightforward consequence of Corollary 4.6 is that graphs ![]() for
for ![]() are not irregular. The natural question is: are the graphs
are not irregular. The natural question is: are the graphs ![]() irregular? The answer is:
irregular? The answer is:
4.7 Theorem. Oriented graphs ![]() are irregular iff n is odd.
are irregular iff n is odd.
Proof. By Theorem 4.2, pairs of vertices ![]() for
for ![]() have the same indegree. Because for the even n the graph
have the same indegree. Because for the even n the graph ![]() is regular, so
is regular, so ![]() is not irregular if
is not irregular if ![]() is even.
is even.
Also by Theorem 4.2, ![]() for
for![]() . By Corollary 4.4, for the odd n the degree sequence of the graph
. By Corollary 4.4, for the odd n the degree sequence of the graph ![]() is of the form
is of the form![]() . So for n odd, if for some two vertices their total degrees are equal then its indegrees are different. Hence
. So for n odd, if for some two vertices their total degrees are equal then its indegrees are different. Hence ![]() is irregular if n is odd. □
is irregular if n is odd. □
Recall that the tournament ![]() is irregular for any n.
is irregular for any n.
5. Density
By density of the graph G, ![]() , we mean ratio “number of edges in the graph G” / “number of edges in complete graph
, we mean ratio “number of edges in the graph G” / “number of edges in complete graph![]() ”; in symbols
”; in symbols![]() .
.
Recall then for every even n, a graph ![]() is
is ![]() -regular. We have
-regular. We have ![]() edges. So for even n,
edges. So for even n,![]() .
.
For every odd n, in a graph ![]() there are
there are ![]() vertices of degree
vertices of degree ![]() and
and ![]() vertices of degree
vertices of degree![]() . We have
. We have ![]() edges. So for odd n,
edges. So for odd n,![]() .
.
Observe that in both cases the density is bigger then 1/2 and
![]()
We have the following:
5.1 Theorem. For![]() ,
,
![]()
Proof. By Corollary 4.5,
![]()
By standard calculation we get
![]()
Recall that![]() , where k and m are fixed, so when
, where k and m are fixed, so when![]() , then also
, then also![]() . So
. So
![]() □
□
Obviously, for![]() ,
,![]() .
.
6. Open Problems
The main open problem concerning k-transitive closures in general, is to state what properties of an oriented graph G guarantee the existence of![]() .
.
There are also some other special classes of oriented graphs, such as cycles (with different orientations) and trees, for which there is a chance to obtain interested properties for their k-transitive closures.
Acknowledgements
We acknowledge the support by the UJK grant No. 612439.
Some of the results contained in this paper were presented at the 5th Polish Combinatorial Conference, Będlewo, September 22-26, 2014. The author wants to express his thanks to Professor Zsolt Tuza for pointing to valuable references.