1. Introduction
CO2 emissions control is a difficult problem since it requires consistent decisions across generations. There are serious conflicts between the generations. For example, as long as individuals’ economic concerns are limited to their own lives, they ruthlessly discount future generations’ wellbeing. Their resultant excessive consumption is certainly connected to excessive emissions of CO2, which have become a serious cause of global warming.
Nevertheless, even though we can overcome such a difficulty in principle, to achieve the precise control requires exorbitant information. By virtue of dynamic programming, we must determine beforehand the terminal condition that corresponds to the wellbeing of generations belonging to the far future in the context of emissions control. Obviously, this is beyond the cognitive ability of human beings.
This study provides an effective control method presuming that the time horizon of an individual is far shorter than the whole length of the time horizon of the history of human beings. Parentage, which implies that love for children does not contradict parents’ own economic concern, plays a crucial role. That is, individuals are assumed to be myopic in the sense that their economic concern is limited to themselves and their children. Parents are called devoted to their children whenever they apply the zero discount rate to the children’s wellbeing. As precisely analyzed below, this is a crucial condition for the global stability of CO2 emissions that requires no information concerning the economic situations of far descendants. That is, the concept of devotion, which is a stronger concept than parentage yet still remains within the cognitive ability of people with common sense, can ultimately hinder excess consumption and emissions that stem from selfish economic motives1.
The rest of paper is constructed as follows. Section 2 deals with a laissez faire economy, in which there is no emissions control, based on the concept of the sequential equilibrium proposed by Kreps and Wilson (1982) [1] . Section 3 defines the first-best emissions control under the stationary state originated by Otaki (2013) [4] . In addition, this section reveals the extent of divergence between the stationary state of the laissez faire economy and that of the properly controlled economy. This fact acutely conveys the importance of CO2 emissions control. Section 4 considers how the economy can reach the first-best allocation without imposing transcendent and stringent morals beyond the cognitive ability of human beings. The concept of parentage and devotion play crucial roles. Section 5 provides brief concluding remarks. Appendix shows the desired property which the transition periods should satisfy, that is dubbed sustainability.
2. The Basic Structure of the Model and the Laissez Faire Economy
2.1. The Basic Structure of the Model
It is assumed that every individual lives in one period, and his or her utility function 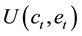 is defined as
is defined as
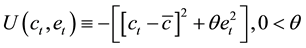 (1)
(1)
where 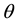 represents how much importance individuals, who belong to generation
represents how much importance individuals, who belong to generation , put on the direct disutility from the accumulated emission of CO2,
, put on the direct disutility from the accumulated emission of CO2, 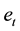 , relatively to current consumption,
, relatively to current consumption,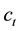 . While such a quadratic function seems quite a naïve formulation, it can exclude inessential phenomena, which are peculiar to nonlinear difference equations, such as limit cycle and chaos, completely. In terms of economics, the nonlinearity, which stems from the complexity of the utility function, is regarded as a less relevant problem compared with the problem that shall be deal with hereafter.
. While such a quadratic function seems quite a naïve formulation, it can exclude inessential phenomena, which are peculiar to nonlinear difference equations, such as limit cycle and chaos, completely. In terms of economics, the nonlinearity, which stems from the complexity of the utility function, is regarded as a less relevant problem compared with the problem that shall be deal with hereafter.
By the same token, the emission dynamics is assumed to obey the following simple linear first order difference equation.
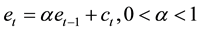 (2)
(2)
2.2. The Laissez Faire Economy as a Sequential Equilibrium
This subsection deals with the consumption/emission dynamics within the laisses faire economy. The laissez faire economy is defined as a sequential equilibrium in the sense of Kreps and Wilson (1982) [1] . That is, it is assumed that generation 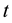 maximizes its utility for a given previously accumulated CO2,
maximizes its utility for a given previously accumulated CO2,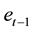 . The first-order condition, which is derived from (1) and (2), implies the following linear difference equation.
. The first-order condition, which is derived from (1) and (2), implies the following linear difference equation.
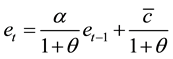 (3)
(3)
It is clear that this equation is stable and monotonously converges to the stationary state:
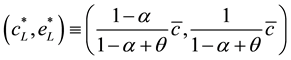 (4)
(4)
The values in (4) comprise the pivotal point for acknowledging the acute necessity for the emissions control.
3. The First-Best Allocation in the Stationary State
This section calculates the first-best allocation of consumption/accumulated emissions in accordance with the method developed by Otaki (2013) [4] . By assuming a proportional carbon tax under the stationary state, it is straightforward from Figure 1 that the marginal substitution rate must be equal to the correct effective relative
price of CO2, 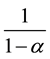 , to the consumption good for achieving the first-best allocation2. This implies the following formula that the optimal planning must satisfy:
, to the consumption good for achieving the first-best allocation2. This implies the following formula that the optimal planning must satisfy:
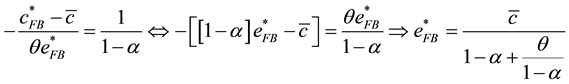 (5)
(5)
Thus, the fist-best allocation at the stationary equilibrium is
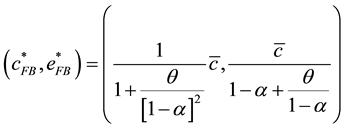 (6)
(6)
Compared with (4), the consumption level of the lasses faire economy exceeds that of the first-best allocation by
![]() (7)
(7)
times. As discussed below, it should be noted that![]() , which is the remaining ratio of CO2 carried over from the previous generation, takes a positive value not far from unity3 [2] [8] . Hence, as long as the emission problem is precarious and
, which is the remaining ratio of CO2 carried over from the previous generation, takes a positive value not far from unity3 [2] [8] . Hence, as long as the emission problem is precarious and ![]() takes a significant value, one must acutely recognize the importance of emissions control.
takes a significant value, one must acutely recognize the importance of emissions control.
4. Parentage as the Minimum Environmental Ethic
The first-best allocation shown in Section 3 imposes quite stringent and transcendent ethics on human beings. Every generation must have deep sympathy for their unforeseen far descendants in order to achieve the idealistic allocation. This criterion is too strict and unfeasible in reality. Instead this section introduces the concept of parentage, which implies that the concern of an individual with well being is limited to those of his/herself and their children. This concept is realistic and coheres with human beings’ cognitive limits in the sense that people can hold sympathy only with the next generation, with whom they can communicate directly. This section analyzes how such parentage contributes to emissions problem.
By using the utility function (1), parentage can be represented as the fact that each individual possesses the following utility function, ![]() , which is contrastive to the sequential equilibrium case in Section 2. That is,
, which is contrastive to the sequential equilibrium case in Section 2. That is,
![]() (8)
(8)
where ![]() is the inverse of the gross discount rate that is applied to the utility of the next generation’s consumption. The utility function (8) implies the emission decision is diversified across generations. It is the current generation’s due to determine the current accumulated CO2 emission,
is the inverse of the gross discount rate that is applied to the utility of the next generation’s consumption. The utility function (8) implies the emission decision is diversified across generations. It is the current generation’s due to determine the current accumulated CO2 emission, ![]() , while future decisions are reserved for future generations. In addition, (8) implies that a generation is not at all directly concerned with the wellbeing of its grandchildren and descendants thereafter. In this sense, such a decision process is myopic. Thus, in some case, the adjustment process towards the stationary state possibly becomes roundabout even though the process is stable.
, while future decisions are reserved for future generations. In addition, (8) implies that a generation is not at all directly concerned with the wellbeing of its grandchildren and descendants thereafter. In this sense, such a decision process is myopic. Thus, in some case, the adjustment process towards the stationary state possibly becomes roundabout even though the process is stable.
The maximization of (8) under the constraint of (2) yields the following second-order difference equation:
![]() (9)
(9)
The eigen value, ![]() , of the corresponding characteristic equation is
, of the corresponding characteristic equation is
![]() (10)
(10)
The corresponding stationary state ![]() is
is
![]() (11)
(11)
It should be noted that, by comparing (11) with (6), the first-best allocation in the stationary state is achieved if parents possess deep parentage enough that they are devoted to their children![]() , as long as the adjustment process is stable. Accordingly, the stability of the economy with such deep parentage as an environmental ethic is a quite important problem. Hereafter, the stability of the economy is defined as follows:
, as long as the adjustment process is stable. Accordingly, the stability of the economy with such deep parentage as an environmental ethic is a quite important problem. Hereafter, the stability of the economy is defined as follows:
Definition 1
The economy is stable if and only if it converges to the stationary state ![]() for any arbitrarily given initial condition,
for any arbitrarily given initial condition,![]() .
.
Such a definition of stability implies that even though the initial parents face unchangeable past accumulation of CO2 within the rational expectations equilibrium, the economy converges to its stationary state if sufficient parentage is embedded to the mind of an individual. In this sense, we, hereafter, search for the minimum ethic that enables the economy to stabilize CO2 emissions autonomously.
Mathematically, Definition 1 is equivalent to the property that the smaller eigen values, ![]() , in (10) should be located within the interval
, in (10) should be located within the interval ![]() 4. Thus, from (10), the necessary and sufficient condition of stability is that
4. Thus, from (10), the necessary and sufficient condition of stability is that ![]() satisfies the following inequality:
satisfies the following inequality:
![]() (12)
(12)
(12) is equivalent to
![]() (13)
(13)
In addition, the following condition is necessary for keeping the stationary state (11) is well defined.
![]() (14)
(14)
The reason why ![]() is contained within the above inequality is that the economy, which corresponds to such case has been already analyzed in Section 2. It should be noted that the egalitarian parentage
is contained within the above inequality is that the economy, which corresponds to such case has been already analyzed in Section 2. It should be noted that the egalitarian parentage ![]() is located within this range. This induces the following theorem concerning the role of parentage in the stability of the economy.
is located within this range. This induces the following theorem concerning the role of parentage in the stability of the economy.
Theorem 1
Parents should be devoted to their children in the sense that they should apply zero social discount rate (i.e.,![]() ) for stabilizing CO2 emission.
) for stabilizing CO2 emission.
Theorem 1 implies that it is an acute environmental ethic for parents to have as much concern for their children’s wellbeing as that for themselves to stabilize emissions of CO2, and this achieves the first-best allocation in the stationary equilibrium although such a long-run problem might be out of their scope.
In addition, some discussions are necessary about the properties of the social discount rate. First, excess devotion is harmful conversely in the sense that parents apply the negative discount rate to their children’s wellbeing at least in the long run. This is because such self-sacrifice thwarts consumption excessively, even though emissions of CO2 are controlled stringently.
Second, although a reliable value of the crucial parameter, ![]() , is not yet obtained, the locally-optimal social discount rate is zero independent of this value. This suggests that even though precise knowledge concerning the circulation mechanism of CO2 is in progress, it is social justice for parents to apply zero discount rate to their children’s wellbeing.
, is not yet obtained, the locally-optimal social discount rate is zero independent of this value. This suggests that even though precise knowledge concerning the circulation mechanism of CO2 is in progress, it is social justice for parents to apply zero discount rate to their children’s wellbeing.
Third, as exhibited in (6) and (11), the allocation approaches the first best together with a decrease in the gross social discount rate ![]() within the range
within the range![]() . This implies that as parents become more benevolent to their children, although not perfectly, more efficient allocation is achieved in the long run.
. This implies that as parents become more benevolent to their children, although not perfectly, more efficient allocation is achieved in the long run.
Finally, although this is the most serious problem, even though the laissez faire economy converges to the stationary state, it should be emphasized that there is no guarantee that such a stationary state is harmonious with the viability of human beings. This implies that not only the parameter of the remaining ratio, ![]() , but also that of awareness of the environment,
, but also that of awareness of the environment, ![]() , play crucial roles for the stability of the atmosphere. In this sense, proper education on the environment is an acute political issue.
, play crucial roles for the stability of the atmosphere. In this sense, proper education on the environment is an acute political issue.
5. Concluding Remarks
This study considers how CO2 emissions should be effectively controlled within the cognitive abilities of human beings. The role of parentage, which is defined as parents’ partial altruism to their children, plays a crucial role. If parentage is perfect, parents are devoted to their children. This means that parents apply zero local social discount rate limited to their children. Then, the first-best resource allocation is achieved in the stable stationary state. Otherwise, some incentive schemes should be constructed for the efficient control of CO2 emissions.
This theorem advocated that artificial carbon tax schemes and/or emissions trading, properties of which are analyzed by Otaki (2013, 2013) [4] [5] , play only subsidiary roles as measures of emissions control. The most important role should be ascribed to the establishment of environmental ethics that are deeply rooted in love for children.
Appendix
Since the problem of stabilizing CO2 emissions contains a serious conflict between generations, it should be some minimum guarantee for the utility acquired by each generation. We dub this guarantee of the minimum utility sustainability. This notion is specifically important when one analyzes the transition path to the stationary state.
In this Appendix, two concepts of sustainability are examined. One is a seemingly egalitarian standard that requires that every generation should enjoy the same utility proposed by Pezzy (1997) [6] and Vanderheiden (2008) [9] in the separate contexts. The other is based on a more stringent definition than Pezzy-Venderheiden’s definition. That is, we call that the economy is sustainable whenever the subsequent generations can enjoy not less utility than current generation. One would find that the equilibrium path derived by this paper satisfies this criterion.
1. Egalitarian Allocation Does Not Imply Justice as Fairness
Sustainability in the sense of Pezzy (1997) [6] and Vanderheiden (2008) [9] does not imply non-discounting future generations’ utility.
Such sustainability is defined by the following egalitarian inequalities:
![]() (1)
(1)
Since under the initial condition
![]()
and the feasibility condition
![]()
(1) requires that the economy should stay at the initial position. That is,
![]() (2)
(2)
It is assumed that the allocation of the economic is initially located at an excess consumption/emission stationary equilibrium, and thus,
![]() (3)
(3)
holds.
The definition of sustainability (1) is advantageous for the initial generation and conservative in the sense that the incumbent interests are reflected as much as possible when the intertemporal emissions allocation is considered. Since the optimized utility of each generation must satisfies
![]() (4)
(4)
And the conditions (2) and (3), the Lagrangean multipliers satisfy
![]() (5)
(5)
(5) implies that the seemingly egalitarian allocation represented by (1), does not mean that the current generation, who plans the emissions control, takes future generations’ utility fairly. Since (1) implies that it makes possible for the current generation, who faces excess consumption/emission, to advocate the status quo even though more desirable allocations exist in the future, the applied social discount rate becomes positive as shown by (5). As such, the progress of emissions control is hindered if we accept the Pezzy-Vanderheiden’s definition of sustainability5 [4] .
2. Priorities of the Value Judgment Concerning CO2 Emissions Control and the Role of Parentage
We assume that value judgments concerning CO2 emissions control obey the following order.
I. An economy must converge to a stable stationary state.
II. The path of CO2 emissions must satisfy the sustainability in the following progressive sense. That is,
![]() (6)
(6)
where ![]() is the utility of a generation in the stationary state. It is also required that inequality holds for at least some
is the utility of a generation in the stationary state. It is also required that inequality holds for at least some![]() . We must note that this condition is stringent than Pezzy-Vanderheiden’s definition of sustainability.
. We must note that this condition is stringent than Pezzy-Vanderheiden’s definition of sustainability.
III. As long as I and II are satisfied, the planning that achieves higher ![]() is desirable.
is desirable.
The first value judgment is imperative for stabilizing the atmosphere and the climate change. The second order judgment concerning sustainability implies that the emissions control should progress incessantly as long as excess consumption/emission prevails in an economy. The third order judgment asserts the importance of the efficiency of the long-run emissions control. An economy will reach the vicinity of the stationary state sooner or later, and stays there during all time thereafter. Accordingly, for the future generations’ wellbeing, this condition should be entailed.
It is already shown the local altruism, which we call parentage, satisfies the conditions I and III. What is left is to check whether such an ingenious emissions control satisfies Condition II. Thus, the following theorem is obtained.
Theorem 2
If ![]() is small enough, the emissions control due to parentage, which is represented by (9) and
is small enough, the emissions control due to parentage, which is represented by (9) and![]() , satisfies Condition II.
, satisfies Condition II.
Proof
By Equation (2), the total derivative of the utility of an individual who belongs to generation ![]() is
is
![]()
From Equation (5) and the assumption, it is clear that
![]() ,
,![]() and
and![]() .
.
Then let ![]() be defined as
be defined as
![]() .
.
By the definition of the eigen value,![]() . On the other hand,
. On the other hand,
![]()
holds. Figure A1 illustrates the locus of![]() . Thus,
. Thus, ![]() holds. Accordingly, if
holds. Accordingly, if ![]() is sufficiently small, such an economy is globally sustainable.
is sufficiently small, such an economy is globally sustainable.
NOTES
1Ramsey (1928) [7] argues that discounting future consumptions is not ethically permissible. He solves the optimal growth path without discounting. My study provides a utilitarian foundation of his assertion. Against Ramsey’s merciful thought, almost all recent research (e.g., Nordhaus (2014) [3] ) presumes the discounting uncritically. This tendency is based on both political and technical reasons. From the political view, the discounting justifies the ephemeral and over consuming prosperity of the current generation to some extent. A technical aspect of model building requires that a utility integral (or summation) over the infinite horizon should remain finite. Without discounting, such a value surely diverges and the analysis becomes meaningless. No discounting is permissible only when a model is formatted based either on the bounded instantaneous utility function (Ramsey’s case) or the limited time horizon for the planning (my case). There seems to be no other attempt to capture the CO2 emissions problem by the infinite chain of individuals whose lives are finite than this study.
![]()
2In addition, evaluating the correct (or socially justified) price of CO2 as 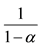 implies that the optimal social discount is unity in the stationary state. For more detail, see Otaki (2013) [4] .
implies that the optimal social discount is unity in the stationary state. For more detail, see Otaki (2013) [4] .
![]()
3According to Tanaka (1993) [8] , CO2 emissions from fossil fuel combustion are estimated at ![]() gigaton and the current absorption ability of oceans is generally estimated
gigaton and the current absorption ability of oceans is generally estimated ![]() gigaton. However, Houghton et al. (1990) [2] report that there serious discrepancy exists in the emission/abruption of CO2of the order of
gigaton. However, Houghton et al. (1990) [2] report that there serious discrepancy exists in the emission/abruption of CO2of the order of ![]() gigaton.
gigaton.
![]()
4By an elementary calculus, it can be ascertained that ![]() takes real values. If people did not abandon the larger eigenvalue,
takes real values. If people did not abandon the larger eigenvalue, ![]() , the value of which possibly exceeds unity, the following vicious cycle would emerge in the economy: higher emissions aggravate the initial condition of the next period. The next generation would be compensated by increasing their consumption further, and this makes the excess emissions problem more serious and so on. It is assumed that individuals are not unwise to be allured by such a devastating consumption explosion.
, the value of which possibly exceeds unity, the following vicious cycle would emerge in the economy: higher emissions aggravate the initial condition of the next period. The next generation would be compensated by increasing their consumption further, and this makes the excess emissions problem more serious and so on. It is assumed that individuals are not unwise to be allured by such a devastating consumption explosion.
![]()
5Otaki (2013) [4] shows that if an economy can converges to the optimal stationary state, the optimal social discount rate becomes zero.