Joule Heating and Thermal Radiation Effects on MHD Boundary Layer Flow of a Nanofluid over an Exponentially Stretching Sheet in a Porous Medium ()
1. Introduction
The industrial processes like hot rolling, wire drawing, spinning of filaments, metal extrusion, crystal growing, glass fibre production, paper production, cooling of a large metallic plate in a bath, which may be an electrolyte, etc. to require the study of flow and heat transfer over a stretching surface. In all these cases, the quality of final product depends on the surface heat transfer rate and the skin friction coefficient. So this study has gained considerable attention in the recent years. Choi [1] was the first to sort heat transfer enhancement upon the invention of “nanofluid”. These fluids are engineered colloidal suspensions composed of nanoparticles in a base fluid. Eastman [2] observed thermal conductivity enhancement in nanofluids. Metals (Al, Cu), oxides (Al2O3, TiO2 and CuO), carbides (SiC), nitrides (AlN, SiN), or nonmetals (graphite, carbon nanotubes) and conductive fluids, such as water or ethylene glycol, or oil, other lubricants, bio-fluids, polymer solutions as base fluids are used in the manufacturing of nanofluids. 5% volume fraction of nanoparticles in these fluids ensure effective heat transfer enhancements which help them to exhibit enhanced thermal conductivity and the convective heat transfer coefficient compared with the base fluid. Routbort [3] found that the typical thermal conductivity enhancements and heat transfer coefficient enhancements are in the range of 15% - 40% and up to 40% over the base fluids. But still there must be other mechanisms to attribute to higher thermal conductivity. Increase in thermal conductivity cannot be considered as the sole reason. Here a survey conducted by Buongiorno [4] on convective transport in nanofluids implied that energy transfer by dispersion of nanoparticles was negligible. His model could not explain the abnormal heat transfer coefficients. The boundary layer has different properties due to the effect of temperature and thermophoresis. There may be a decrease in viscosity in the boundary layer, which will lead to heat transfer enhancement. Many other literatures support Buongiorno’s explanation. An excellent assessment of nanofluid physics and developments had been provided by Cheng [5] and Ali [6] . Buongiorno and Hu [7] observed that although convective heat transfer enhancement had been suggested to be due to the dispersion of the suspended nanoparticles, this effect was too small to explain the observed enhancement.
It is often assumed in the problems of boundary layer flow over a stretching surface that the velocity of the stretching surface is linearly proportional to distance from the fixed origin. However, Gupta [8] had argued against the linearity condition. In the real world problem, the stretching of plastic sheet may not necessarily be linear. For example an exponentially stretching sheet was considered by Sanjayanand [9] . Heat and mass transfer on its boundary layers are investigated. Suction and heat transfer characteristics were addressed by Youn [10] . Heat transfer in a viscoelastic boundary layer flow over a stretching sheet with viscous dissipation and non-uniform heat source was studied by Subhas [11] . Thermal radiation effect on the flow was examined by Sohail Nadeem [12] . Anuar Ishak [13] studied the MHD boundary layer flow due to an exponentially stretching surface having the effect of radiation. Effect of magnetic field on boundary layer flow and heat transfer of a dusty fluid with an exponential temperature distribution on the exponentially stretching sheet was considered by Al-odat [14] .
Hitesh Kumar [15] worked on the heat transfer MHD boundary-layer flow through a porous medium. Gopi Chand [16] considered an unsteady stretching surface in a porous medium and explained the viscous dissipation and Radiation effects on MHD flow over it. Flow through a porous medium bounded by a vertical surface in presence of hall current was explained by Sudhakar [17] . joules DISSIPATION over a nonlinear vertical stretching porous sheet was introduced by Subhas Abel [18] . M.M. Hamza [19] provided the study of Oscillatory Flow through a porous medium. P.R. Sharma [20] worked on a porous stretching sheet.
This paper provides the solution to the problem of flow and heat transfer of a nanofluid over an exponentially stretching porous sheet by considering the effect of chemical reaction, joule heating and thermal radiation parameters along with the suction parameter by adopting the Keller Box method.
2. Formulation of the Problem
The present problem is based on a steady two-dimensional incompressible viscous laminar flow of an electrically conducting nanofluid over a permeable exponentially stretching sheet in a porous medium as shown in Figure 1. The X-axis is taken along the stretching surface in the direction of motion and the Y-axis is perpendicular to it. The flow is confined to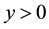 . Two equal and opposite forces are applied along the X-axis. Keeping the origin fixed, the sheet is then stretched with a velocity
. Two equal and opposite forces are applied along the X-axis. Keeping the origin fixed, the sheet is then stretched with a velocity , varying exponentially with the distance from the slit. It is assumed that the surface temperature
, varying exponentially with the distance from the slit. It is assumed that the surface temperature 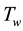 and nanoparticle fraction
and nanoparticle fraction 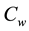 are constants and they differ from the ambient values of temperature and nanoparticle fraction
are constants and they differ from the ambient values of temperature and nanoparticle fraction 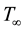 and
and , respectively. The usual boundary layer approximations are still applicable. The governing equations of continuity, momentum, energy and concentration in Cartesian coordinates x and y are:
, respectively. The usual boundary layer approximations are still applicable. The governing equations of continuity, momentum, energy and concentration in Cartesian coordinates x and y are:
 (1)
(1)
![]()
Figure 1. Physical modal and coordinate system.
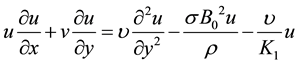 (2)
(2)
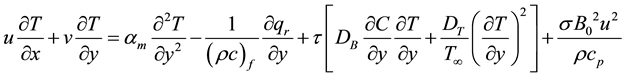 (3)
(3)
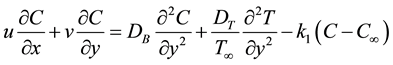 (4)
(4)
where, u & v are the velocity components in X and Y-directions respectively, ρ-density of the nanofluid, B0-in- duced magnetic field, σ-electrical conductivity, υ-kinematic viscosity, K1-thermal conductivity, αm-thermal diffusivity parameter, (ρc)f-the heat capacitance of the base fluid, τ-ratio between the effective heat capacity of the nanoparticle material and heat capacity of the nanofluid, DB-the Brownian diffusion coefficient, DT-the thermophoresis coefficient, qγ-radiative heat flux, k1-chemical reaction parameter, cp-specific heat capacity of the nanoparticle, γ-chemical reaction parameter, α-the chemical reaction coefficient, T-temperature of the nanofluid, C-concentration of the nanofluid, Tw and Cw-the temperature and concentration along the stretching sheet, 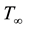 and
and 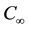 -the ambient temperature and concentration.
-the ambient temperature and concentration.
The boundary conditions are:
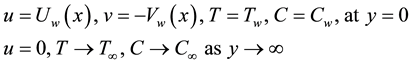 (5)
(5)
By using the Rosseland approximation for radiative heat flux is defined as:
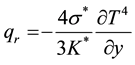 (6)
(6)
where 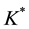 is the mean absorption coefficient and
is the mean absorption coefficient and ![]() is the Stefan-Boltzmann constant. Since the temperature differences within the flow field are assumed to be small, and then we linearize and expand
is the Stefan-Boltzmann constant. Since the temperature differences within the flow field are assumed to be small, and then we linearize and expand ![]() into the Taylor series about
into the Taylor series about![]() , which after neglecting higher order forms takes the form.
, which after neglecting higher order forms takes the form.
![]() (7)
(7)
To examine the flow, the following transformations are used:
![]() (8)
(8)
To determine the velocity, temperature distribution and rate of heat and mass transfer in the above boundary layer (5), we solve the equations related to the stretching sheet problem to obtain the following similarity equations using (8). In deriving these equations, the external electric field is assumed to be zero and the electric field due to polarization of charges in negligible.
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
The transformed boundary conditions take the following forms:
![]() (12)
(12)
where,
![]() (13)
(13)
For the type of boundary layer flow, the skin-friction coefficient, heat transfer coefficient and mass transfer coefficients are important physical parameters.
They defined as:
![]() (14)
(14)
The dimensionless forms of these parameters are:
![]() (15)
(15)
where the surface shear stress![]() , the surface heat flux
, the surface heat flux![]() , the surface mass flux
, the surface mass flux ![]() and
and ![]() is the Reynolds number with
is the Reynolds number with ![]() and
and ![]() being the dynamic viscosity
being the dynamic viscosity
and the thermal conductivity, respectively. The numerical values of![]() ,
, ![]() and
and ![]() are proportional to the local skin-friction coefficient, local Nusselt number and local Sherwood number respectively and these are presented by Table 1 for the values of the physical parameters.
are proportional to the local skin-friction coefficient, local Nusselt number and local Sherwood number respectively and these are presented by Table 1 for the values of the physical parameters.
3. Numerical Solution
Equations (9)-(11) subjected to the boundary conditions (12) are solved numerically using implicit finite difference method that is known as Keller Box in combination with the Newton’s techniques as described by Cebeci and Bradshaw [21] . This method is unconditionally stable and has second order accuracy.
![]()
Table 1. Comparison of results for ![]() with previous published works.
with previous published works.
The principal steps in using the Keller Box method are:
1) Reducing higher order ODEs (systems of ODES) in to systems of first order ODEs;
2) Writing the systems of first order ODEs into difference equations using central differencing scheme;
3) Linearizing the difference equations using Newton’s method and wring it in vector form;
4) Solving the system of equations using block elimination method.
In order to solve the above differential equations numerically, we adopt Matlab software which is very efficient in using the well known Keller Box method. In accordance with the boundary layer analysis, the boundary condition (12) at ![]() is replaced by
is replaced by![]() , and the step size
, and the step size ![]() is used to obtain numerical solu-
is used to obtain numerical solu-
tion with five decimal place accuracy as the criterion of convergence. Obtained coupled ordinary non-linear Equations (9)-(11) are solved by Keller Box method for boundary condition (12). Accuracy of this numericalmethod shown in Table 1 is being validated by direct comparison with the numerical results reported by N.G. Rudraswamy [22] , Meraj Mustafa et al. [23] . The numerical comparisons of, ![]() ,
, ![]() and
and ![]() for the values of Pr, Le, S, γ, R, Nt, Nb, M, G and H are shown in Table 2.
for the values of Pr, Le, S, γ, R, Nt, Nb, M, G and H are shown in Table 2.
4. Results and Discussion
Referring from Figure 2 larger Prandtl number has a relatively lower thermal diffusivity. This is because Pris defined as the ration of kinematic viscosity to thermal diffusivity. Thus an increase in Pr reduces thermal diffusivity; it decreases the thermal boundary layer thickness. Consequently, increases rate of heat transfer, and thereby increases the variation in the thermal characteristics. As expected, the variation in the temperature is more pronounced for smaller values of Pr than its larger values.
Figures 3-5 depict the effects of suction parameter S on velocity, temperature and concentration profiles, respectively at the boundary for exponentially stretching sheet. It is observed that velocity decreases significantly with increasing suction parameter where as fluid velocity is found to increase with blowing. It is observed that, when the wall suction (S > 0) is considered, this causes a decrease in the boundary layer thickness and the velocity field is reduced. Opposite behaviour is noted for blowing S < 0. In Figure 4, it is seen that temperature decreases with increasing suction parameter where as it increases due to blowing. Temperature overshoot is noted for blowing (S < 0) this feature prevails up to certain heights and then the process slowed down and at a far distance from the wall temperature vanishes. In Figure 5, it is observed that concentration decreases with increasing suction parameter where as it increases due to blowing.
Figure 6 shows the effect of Le on the dimensionless concentration for fixed values of other parameters. It is observed that for larger values of Le suppress the concentration profile i.e. inhibit nanoparticle species diffusion, as observed. There will be a much greater reduction in the concentration boundary layer thickness.
Figures 7-10 show that an abnormal increase in the concentration ![]() is found for a weaker Brownian motion Nb in fact an over shoot in the concentration function occurs Nt increases gradually. The effect is seen in the case of temperature profile. An appreciable increase in temperature profile is found for increasing values of Nt. In this case, an increase in temperature is found with increasing values of Nb.
is found for a weaker Brownian motion Nb in fact an over shoot in the concentration function occurs Nt increases gradually. The effect is seen in the case of temperature profile. An appreciable increase in temperature profile is found for increasing values of Nt. In this case, an increase in temperature is found with increasing values of Nb.
Figure 11 and Figure 12 exhibits the nature of velocity field for the variation of magnetic parameter M. With increasing M, velocity is found to decrease but the temperature increases. As the Lorentz force opposes the motion of the fluid, much fluid is not entering to the boundary layer. It enforces the thickening of thermal layer.
As shown in Figure 13, it is observed that the nanoparicle volume fraction decreases with increasing values of chemical reaction parameter whereas the velocity and temperature profiles are not significant with the chemical reaction parameter.
As depicted in Figure 14, it is noticed that an increase in R yields an increase in the nanofluid’s temperature,
![]()
Table 2. Showing results of![]() ,
, ![]() and
and ![]() for the values of Pr, M, S, Le, R, γ, G, H, Nt, and Nb.
for the values of Pr, M, S, Le, R, γ, G, H, Nt, and Nb.
which leads to decrease in the heat transfer rate. Thus, the radiation should be at its minimum in order to facilitate the cooling process. All these physical behaviour are due to the combined effects of the strength of the Brownian motion and thermophoresis particle deposition.
Figure 15 and Figure 16, show effect of porosity parameter G on the temperature and velocity profiles, respectively. It is observed that the presence of the porous medium. The temperature profile whereas is reduces the velocity profile. This is because the porous medium inhibits the fluid not to move freely through the boundary layer. This leads the flow to increase thermal boundary layer thickness.
As shown in Figure 17 and Figure 18, it is observed that an increase in joule heating parameter H the
![]()
Figure 2. Variation of temperature θ(η) with η for several values of Prandtl number Pr.
![]()
Figure 3. Variation of velocity ![]() with η for several values of suction parameter S.
with η for several values of suction parameter S.
![]()
Figure 4. Variation of θ(η) with η for several values of suction parameter S.
![]()
Figure 5. Variation of concentration ϕ(η) with η for several values of suction of S.
![]()
Figure 6. Variation of concentration ϕ(η) for with η for several values of Lewis number Le.
![]()
Figure 7. Variation of temperature θ(η) with ηseveral values of thermophoresis parameter Nt.
![]()
Figure 8. Variation of temperature θ(η) with η for several values of Brownian motion Nb.
![]()
Figure 9. Variation of concentration of ϕ(η) with η for several values of thermophoresis parameter Nt.
![]()
Figure 10. Variation of concentration of ϕ(η) with η for several values of Brownian motion parameter Nb.
![]()
Figure 11. Variation of temperature θ(η) with η for several values of magnetic parameter M.
![]()
Figure 12. Variation of velocity ![]() with η with several values of Magnetic parameter M.
with η with several values of Magnetic parameter M.
![]()
Figure 13. Variation of concentration ϕ(η) with η for several values of chemical reaction parameter γ.
![]()
Figure 14. Variation of temperature θ(η) with η for several values of thermal radiation parameter R.
![]()
Figure 15. Variation of temperature θ(η) with η for several values of porosity parameter G.
![]()
Figure 16. Variation of velocity ![]() with η for several values of porosity parameter G.
with η for several values of porosity parameter G.
![]()
Figure 17. Variation of concentration (η) with η for several values of joule heating effect H.
![]()
Figure 18. Variation of temperature θ(η) with η for several values of joule heating effect H.
profiles for temperature and concentration are decreasing.
5. Conclusions
A numerical study corresponding to the flow and heat transfer in a steady flow region of nanofluid over an exponential stretching surface and effects of chemical reaction, thermal radiation, magnetic, suction parameter, porosity parameter and joule heating parameters is examined and discussed in detail. The main observations of the present study are as follows.
An increase in suction parameter leads the velocity, temperature and concentration profiles to decrease. For larger values of Le suppress the concentration profile i.e. inhibit nanoparticle species diffusion, as observed. There will be a much greater reduction in the concentration boundary layer thickness. As Nt increases, temperature profile increases but the concentration profile decreases. With increasing values of Nb, both temperature and concentrations profiles increase. As increase in chemical reaction paramter γ leads the concentration profiles to decrease. The impact of porosity parameter shows that velocity profile is decreasing and temperature profile is increasing. This is because the porous medium inhibits the fluid not to move freely through the boundary layer. This leads the flow to increase thermal boundary layer thickness. Joule heating parameter reduces the temperature and concentration of nanofluid.