Economic Load Dispatch Based on Efficient Population Utilization Strategy for Particle Swarm Optimization ()
1. Introduction
Economic load dispatch is one of the important fundamental issues in power systems operation and planning. From solving that problem, fuel cost can be reduced and the reliability of the power system can be improved. The fundamental objective of the optimization problem is to minimize the cost of power generation by determine the output power of generating units with satisfying the load demand, operational requirement and other constraints. From past researches, we can know that due to the existing of valve point effect [1] , the unit input-output curves of generators is with characteristics of non-linear, non-convex and non-derivable. Taking the distribution network transmission capacity constraints and system stability requirements into account, the formula of ELD problems turns non-differentiable and non-derivable [2] . What’s more, there are a larger number of units in distribution system, and making the input-output function of units has higher dimension and lots of local optimization solutions [3] . Therefore, in order to maintain multidimensional and high accuracy, the classical assignment optimization algorithm, such as Dynamic Programming [4] , Linear Programming [5] etc, have already been unable to solve ELD optimization problems well.
In recent years, various kinds of intelligent algorithms are widely used in ELD optimization because of their good global convergence and non-restricting by the object function, which include ant colony algorithm, simulated annealing algorithm, chaos algorithm and so on (Thesis [3] considers the constrained optimization of the non-convex nonlinear system, which can apply the generalized ant colony algorithm to the problem of ELD optimization successfully, and proves the convergence of the algorithm. Thesis [6] applies self-adjusting particle swarm optimization algorithm to ELD optimization problems, overcomes the premature convergence of PSO and improves the accuracy of the optimal solution. Thesis [7] introduces the chaos optimization method to the ELD optimization problem).
Particle swarm optimization (PSO) was a biological evolution method which was proposed by Kennedy and Eberhart in 1995 [8] . It has many advantages that include the fast speed of convergence, and the need for the parameters is less and easy to achieve. However, when PSO is applied to the multidimensional and complex optimization problem, it will be easy to converge and fall into local optima. For this reason, significant researches have been conducted on PSO and many improved algorithms have been proposed. In this paper, we propose to use an EPUSPSO to solve the ELD problem which has the advantages in global convergence, making the particles to be effective in locating the optimal point, and better convergence effect. It is proved successfully in comparing with other PSO optimization under different dimensional conditions and simulating of IEEE 3, 13 and 40 units system with considering of valve point effect.
2. Economic Load Dispatch Problem Formulation
In power systems, Economic load dispatch (ELD) is a method to schedule the power generator outputs with respect to the system constraints. Power system has to be optimized in such a way that it finally supplies all the loads with minimum fuel costs. Mathematically, the economic load dispatch problem function can be summarized as follows:
 (1)
(1)
where,
F = total fuel cost;
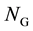 = the number of generators in the system;
= the number of generators in the system;
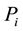 = the output active power of i-th generator;
= the output active power of i-th generator;
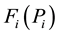 = the cost function of i-th generator.
= the cost function of i-th generator.
In the unit “heat run” testing stage, the cost function of single generator can be obtained, which can be presented by a quadratic cost function as follows:
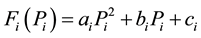 (2)
(2)
where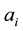 ,
, 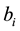 and
and  denote the cost coefficients of the i-th generator.
denote the cost coefficients of the i-th generator.
When the turbine admission valve at low level starts to open, the effect of wire drawing produce a rippling effect on the unit, this is called the valve point effect. If the valve point effect is neglected, there will be significantly affect the accuracy of the solution. When taking the ripples to valve point effect into consideration, the cost function becomes:
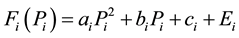 (3)
(3)
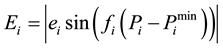 (4)
(4)
where,
 = the change influenced by valve point effect;
= the change influenced by valve point effect;
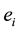 ,
, 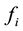 = cost coefficients of i-th generator corresponding to valve point loading;
= cost coefficients of i-th generator corresponding to valve point loading;
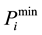 = the minimum operating output of i-th generator.
= the minimum operating output of i-th generator.
Generator capacity should be satisfied:
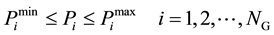 (5)
(5)
where, 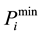 and
and ![]() are the minimum and maximum power outputs of unit i.
are the minimum and maximum power outputs of unit i.
The power balance must meet the constraints as follows:
![]() (6)
(6)
where,
![]() = the transmission loss;
= the transmission loss; ![]() = the system load demand.
= the system load demand.
In this paper, distribution network in the power system are concentrated, so the transmission losses can be neglected. As the system is a multi-unit power system with high dimension in this paper, the constraint can be simplified as follows:
![]() (7)
(7)
3. EPUSPSO Approach
3.1. PSO
Particle swarm optimization (PSO) is a biological evolution method inspired by the social behavior of animals (flock of birds), PSO is based on the concept of swarms and their intelligence and movement. A swam of particles represent a potential solution to the optimization problem. In the iterative process, each particle adjusts its position in term of its own experience, and the experience of its neighborhood particles at each time step. In other words, in PSO algorithm, particles can share information among individuals, start with a random population initialization and end with fast convergence to acceptable solution in the search space.
3.2. EPUSPSO
Efficient population utilization strategy for particle swarm optimization (EPUSPSO) [9] is a kind of enhanced particle swarm optimization by using variable particles in swarms to strength the searching ability. In this paper, the EPUSPSO is proposed to solve the ELD problems in power system. In order to overcome the difficulties of different ELD problems the appropriate adjustments and improvements are done in the programming. The algorithm begins by initializing a group of random particles (random solutions), and then find the optimal solution through an iterative process. In every step of iteration, each particle adjusts its position according to two extreme values. One optimal solution find by its own experience, which is called Pbest. The other optimal solution got by experience of its neighborhood particles, which is called Gbest.
![]() (8)
(8)
![]() (9)
(9)
where, x means the current position of individuals, and v means the current velocity of individuals. i and j mean the j-th dimension of the i-th particle. s and w are set as the current number of iterations and the weight parameter respectively, c is set as the learning factor and r is a random number between 0 and 1.
Equation (8) is the speed function, it means that each particle in the iterative process in accordance with two extreme values of the optimal solution to update their own pace. Equation (9) is the location function, by which particles update their location and got the optimal solution after numbers of iteration.
Although the PSO algorithm can solve multi-variable optimization problem, but it is easy to fall into local optima in solving problems of high complexity, usually in later iterations, ordinary particle swarm algorithm can’t obtain a faster convergence effect. But the EPUSPSO can finish good optimization without these problems.
EPUSPSO algorithm is an enhanced particle swarm algorithm using variable particles and the biggest improvement is to change the number of particles effectively by changing global optimization values. This method is called solution-sharing strategy. Content rules are as follows:
1) If the fitness value of global optimal solution has not been updated in two consecutive generations, then add a particle in the population.
![]() (10)
(10)
Coefficient ![]() and
and ![]() are the serial number of the two particles selected from the current population randomly.
are the serial number of the two particles selected from the current population randomly.
2) If the fitness value of global optimal solution is updated in two consecutive generations. It means the existing particles are enough to handle the current solution searching procedures and then remove the particle from swarm population which has lower fitness value.
In addition, the algorithm adopts searching range sharing strategy and solution sharing strategy. In order to prevent the particles from falling into the local minimum, the activation probability of the search range sharing strategy could be defined as Pr(s) and the formula is as follows:
![]() (11)
(11)
where, iteration in the formula means the maximum iteration.
The search range sharing strategy is used to reset all dimensions of individual particles’ current positions in the solution space. It can be divided into two different kinds of patterns according to the different searching space, that is the global pattern and the local pattern. In the global pattern, particles are restricted in the search boundary as (xmin, xmax) initially. In the local pattern, searching space boundary is restricted in past best solution (Pbestmin, Pbestmax). Selected from the individual optimal solution, Pbestmax is the maximum solution and the Pbestmin is the minimal solution.
At the same time, the singularity the existing particle velocity update process has improved by the setting of solution sharing strategy and the calculation formula is as follows:
![]() (12)
(12)
In the formula, coefficient a represents a random serial number of a particle from the population and rand is a random number between 0 and 1. The formula Psi is as follows:
![]() (13)
(13)
where, D is the dimension of the particle.
4. Numerical Results
For evaluating the advantages and applicability of the proposed EPUSPSO method in dealing with different- dimensional, non-convex, non-conducting and multi-constrained optimization problems, tests are made through three different dimensions of typical ELD problems. Of all the test cases, valve-point loading effect of the ripple curve is considered and the transmission loss is neglected. For this work, MATLAB R2013a is used, all parameter of generators in cases below can be obtained in reference [10] , and every result of the cases will be compared with other intelligent algorithms [11] [12] , such as IGA [13] , MPSO [14] , and CEP [10] [15] . The algorithm are tested 100 times separately under the same condition in the different ELD cases, the maximum cost (Fmax), the minimum cost (Fmin), and the average cost (Fmean) are acquired from the tests, and the results from other algorithms can be acquired from the references.
Case 1: The first test system consists of 3 thermal generating units with 6 bus bars by simulation. The expected load demand for this test case is 850 MW. The value of population size is 64. The dimension of the test is set to 3. Different methods are tested on the same system. Comparison of cost and the convergence characteristics are illustrated in Figure 1 and Table 1.
In Figure 1, we can see that the EPUSPSO converges faster when deals with 3-generator ELD problem. In Table 1, EPUSPSO cost less compared to other intelligent algorithms, indicating that the algorithm have at an optimal solution on solving low-dimensional problems.
Case 2: The proposed method is also tested on the 13-unit system. The difference is that the expected load demand for this test case is 1800 MW, and the dimension is 13. Other parameters are the same as Case 1. The comparison of the convergence characteristics of various methods is demonstrated as follow, simulation results are shown in Figure 2, and different methods tested on the same system are also compared and illustrated in Table 2.
It can be seen in Table 2, the convergence rate of EPUSPSO algorithm is faster than other algorithms when the dimension is higher. Comparison of the data in Table 2 reveals that the optimal solution is better and reliability of EPUSPSO algorithm is higher.
Case 3: In this section, EPUSPSO method is applied to a 40-generator system. The expected load demand for this test case is equal to 10,500 MW, and the dimension is 40. Other parameters are the same as Case 1. Figure 3 presented the convergence characteristics and Table 3 demonstrates the solutions in comparison with the other approaches available in references.
The data in Figure 3 shows that the ability of the EPUSPSO in finding the optimization solution is more efficient. The comparison in Table 3 reveals that EPUSPSO performed better, and can be applied to engineering projects.
From three cases above, we can see that EPUSPSO outperformed both accuracy and convergence speed of solution. No matter the dimension is lower or higher, EPUSPSO has good stability. With its advantages, the EPUSPSO algorithm is suitable for solving the optimization problems of ELD in large power systems.
![]()
Table 1. Results comparison of Case 1.
![]()
Table 2. Results comparison of Case 2.
![]()
Table 3. Results comparison of Case 3.
![]()
Figure 1. Convergence comparison of EPUSPSO and PSO in this Case 1.
![]()
Figure 2. Convergence comparison of EPUSPSO and PSO in this Case 2.
![]()
Figure 3. Convergence comparison of EPUSPSO and PSO in this Case 3.
5. Conclusion
In this paper, we use EPUSPSO to solve different-dimensional and non-convex and nonlinear constraints problems in ELD. Compare with the traditional PSO, the algorithm overcomes the shortcomings of PSO algorithm that is easy to fall into local optima and the global optimal solution can be found in the optimization problem to a large extent. In the meantime, EPUSPSO has the faster speed of convergence, the higher accuracy and it is easy to achieve. Then we put this algorithm in an actual ELD problem to simulation which is considered the valve point effect, line capacity constraint and system stability constraints of generator units and the results demonstrate the feasibility and effectiveness of the proposed algorithm. We can also use this algorithm to other complex optimization problems in virtue of its universal property.