Serial Genetic Algorithm Decoder for Low Density Parity Check Codes ()
1. Introduction
The current large development and deployment of wireless and digital communication encourage the research activities in the domain of error correcting codes. The latter is used to improve the reliability of data transmitted over communication channels susceptible to noise. Coding techniques create codewords by adding redundant information to the user information vectors. Decoding algorithms try to find the most likely transmitted codewords related to the received one as depicted in Figure 1.
Decoding algorithms are classified into two categories: hard decision and soft decision algorithms. Hard decision algorithms work on a binary form of the received information. In contrast, soft decision algorithms work directly on the received symbols [1] . Soft-decision decoding is a NP-hard problem and has been approached in different ways. Recently artificial intelligence techniques were introduced to solve this problem. Among the related works, the decoding of linear block codes uses algorithm A* [2] , genetic algorithms [1] [3] and neural networks [4] .
LDPC codes were invented by Gallager [5] in his PhD thesis. Soon after their invention, they were largely
forgotten, and reinvented several times for the next 30 years. Their comeback is one of the most intriguing aspects of their history, since two different communities’ reinvented codes are similar to Gallager’s LDPC codes at roughly the same time, but for entirely different reasons.
Low Density Parity Check (LDPC) codes are a class of linear block codes. The name comes from the characteristic of their parity-check matrix which contains only a few 1’s in comparison to the amount of 0’s. Their main advantage is that they provide a performance which is very close to the capacity for a lot of different channels and linear time complex algorithms for decoding. Furthermore, they are suited for implementations that make heavy use of parallelism [6] .
LDPC codes have emerged as the best error correcting codes close to the theoretical Shannon limit performance. When these codes are decoded using Gallager’s iterative probabilistic decoding method, also known as the sum-product algorithm or belief propagation algorithm, their empirical BER performance is found to be excellent [7] - [9] . This is true when the length of the code vector is large enough.
The LDPC sum-product decoding algorithm [5] [10] makes an estimation of the A Posteriori Probability (APP) of each symbol as a function of the received symbol and the properties of the channel. In this sense, the decoding algorithm is required to know the signal-to-noise ratio in the channel.
In this article we introduce a new Serial Genetic Algorithm Decoder (SGAD) LDPC codes. In effect, a comparison with sum-product decoder, which is currently the most successful algorithm for LDPC, shows its efficiency, and gives the higher performances.
This paper is organized as follows. In Section II, we introduce Genetic algorithm; in Section III, we present SGAD (our decoder) and analyze the performances. Finally, Section IV presents the conclusion and future trends.
2. Genetic Algorithm
Genetic algorithms are heuristic search algorithms premised on the natural selection and genetic [3] [11] [12] . It is a non-mathematical, non-deterministic, but stochastic process or algorithm for solving optimization problems. The concept of genetic algorithm was introduced by Holland [13] in 1975, it is defined by:
・ Individual or chromosome: a potential solution of the problem, it’s a sequence of genes.
・ Population: a set of points of the research space.
・ Environment: the space of research.
・ Fitness function: the function to maximise/minimise.
・ Encoding of chromosomes: it depends on the treated problem, the famous known schemes of coding are: binary encoding, permutation encoding, value encoding and tree encoding.
・ Operators of evolution:
Selection: It permits to select the best individuals to insert in the intermediate generation.
Crossover: For a pair of parents (p1; p2) it permits to create two children (ch1; ch2), with a crossover probability Pc.
Mutation: The genes of the individual are muted according to the mutation rate mr and the mutation probability Pm. The typical steps in the design of genetic algorithm are described below and illustrated in Figure 2:
![]()
Figure 2. A simplified model of a genetic algorithm.
3. Serial Genetic Algorithm Decoder (SGAD)
This work is a serialization of the genetic algorithm, the decoder computes the syndrome of the received vector, so if the syndrome is null, the decoder returns the decoded vector equal to the binary decision of received one, else the decoder turn the first execution of GA with an initial population randomly generated (PoP), in the second execution of GA, the decoder inserts a subpopulation (SubPoP) (a some elites of the last generation for first GA execution) in the initial population (PoP). Then the decoder returns the best individuals as a decoded word. The pseudo code of SGAD is shown in Figure 3. The parameters are the population size (Ni); the subpopulation size (p), the number of generation (Ng).
3.1. The SGAD Decoder
Let C a Low Density Parity Check (LDPC) code, and let 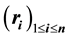 be the received sequence over a communication channel with noise variance
be the received sequence over a communication channel with noise variance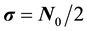 , where
, where  is noise power spectral density.
is noise power spectral density.
Let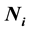 ,
, 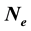 and
and 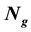 respectively, the population size, the number of elite members, the number of generations
respectively, the population size, the number of elite members, the number of generations
Let P the size of the subpopulation.
Let 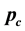 and
and 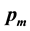 be the crossover and the mutation rates.
be the crossover and the mutation rates.
Let U = [0,1] and 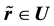 is the received vector transformed into [0,1] using the hyperbolic tangent sigmoidal function (Equation (3)).
is the received vector transformed into [0,1] using the hyperbolic tangent sigmoidal function (Equation (3)).
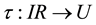 (1)
(1)
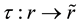 (2)
(2)
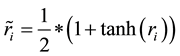 (3)
(3)
The decoding-based on serial genetic algorithm is depicted in Figure 3. The steps of the decoder based on SGA are as follows:
Step 1. The decoder calculates de syndrome of de received vector (Equation (4)).
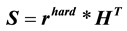 (4)
(4)
where 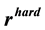 is the hard decision of
is the hard decision of ![]() (Equation (5)), and
(Equation (5)), and ![]() is the transpose of the matrix
is the transpose of the matrix![]() .
.
![]() (5)
(5)
If![]() , then a valid code vector
, then a valid code vector ![]() is obtained by
is obtained by![]() . Otherwise we apply the steps of GA:
. Otherwise we apply the steps of GA:
Step 2. Generate an initial random subpopulation (SubPoP) of ![]() soft vectors
soft vectors ![]() of
of ![]() components (
components (![]() ).
).
Step 3. For i from 1 to 2.
Substep 3.1. Generate an initial random population (PoP) of ![]() soft vectors
soft vectors ![]() of
of ![]() components (
components (![]() ).
).
Substep 3.2. Insert the subpopulation (SubPoP) in the initial population (PoP).
Substep 3.3. Compute the fitness of each individual in the population:
The fitness function is the syndrome weight of de candidate, and the distance between the candidate vector and the received one (Equation (2)).
![]() (6)
(6)
where
![]() (7)
(7)
and
![]() (8)
(8)
z is the solution provided by GA.
![]() and
and![]() , denote, respectively, the number of rows of the parity check matrix
, denote, respectively, the number of rows of the parity check matrix![]() , the code vector length.
, the code vector length.
Substep 3.4. The population is sorted in ascending order of member’s fitness defined by (6).
Substep 3.5. The best two members (![]() ) of each generation are inserted in the next one.
) of each generation are inserted in the next one.
Substep 3.6. The other ![]() members of the next generation are generated as follows:
members of the next generation are generated as follows:
Subsubstep 3.6.1. Selection operation: a selection operation that uses the tournament selection method is applied in order to identify the best parents![]() , on which the reproduction operators are applied.
, on which the reproduction operators are applied.
Subsubstep 3.6.2. Crossover operation: Create new vectors ![]() “children”, with a given probability rate
“children”, with a given probability rate![]() . We use Ring Crossover (RC) [14] .
. We use Ring Crossover (RC) [14] .
Subsubstep 3.6.3. Mutation operator: To complete the new generation, children are mutated by introducing random changes with a given probability rate ![]() to single parent.
to single parent.
The P best member from the last generation for the first execution of GA are inserted in the subpopulation (SupPoP).
Step 4. The decoder decision is z the best member from the last generation after two GA runs.
3.2. Simulation Results and Discussions Related to SGAD
In order to prove the effectiveness of SGAD, we do intensive simulations.
The simulations where made with default parameters outlined in Table 1. The performances are given in terms of BER (bit error rate) as a function of SNR (Signal to Noise Ratio Eb/N0).
3.2.1. Effect of the Subpopulation Size on the Performance
The number of size of the subpopulation (the number of the elites members of the last generation inserted in the initial population for second execution of GA) used in our decoder has an effect in the performances quality. Figure 4 shows this effect.
Figure 4 shows that the performance improves by increasing the number of size of the subpopulation until 20, after, the performance decrease by increasing this number. So the number of size of the subpopulation must be chosen carefully to give good impact into the performances of our decoder.
3.2.2. Comparison with Sum-Product Decoder
Our new decoder has been compared with the Sum-Product Decoder for regular LDPC (63,37), LDPC (73,45) and
![]()
Figure 4. Performance of our decoder for different size of the subpopulation.
LDPC (96,48) codes. The results are given in Figures 5-7:
Figure 5 shows that the SGAD provides good performances compared to sum-product decoder for regular LDPC (63,37) code. The gain between the SGAD and sum-product decoder is 1.5 dB at 10−4.
Figure 6 compares the performances of SGAD with sum-product decoder for regular LDPC (73,45) code. We remark that the SGAD is better than sum-product decoder. The gain between the SGAD and sum-product decoder is 1.5 dB at 10−4.
Figure 7 compares the performances of SGAD with sum-product decoder. We remark that the SGAD is better than sum-product decoder for regular LDPC (96,48) code. The gain between the SGAD and sum-product decoder is 1 dB at 10−3.
3.2.3. Study of Hyperbolic Tangent Sigmoidal Function
We have used the hyperbolic tangent function (Equation (3)) in our decoder based on serial genetic algorithm for transform the values of the received vector (r) in domain [0,1]. We have taken the value of the received word r in the interval [−4,4], and we have plotted the transformation using the hyperbolic tangent function (Figure 8).
From this figure we can say that the tangent hyperbolic function, applied component wise, is to map the components of the received vector ![]() into [0,1] Also, shows that for one r lower than zero, when we increase the factor
into [0,1] Also, shows that for one r lower than zero, when we increase the factor![]() ,
, ![]() close to zero, and for one r is greater than 0, when we increase the factor
close to zero, and for one r is greater than 0, when we increase the factor![]() ,
, ![]() close to one. we can conclude that, by reducing the value of the factor
close to one. we can conclude that, by reducing the value of the factor ![]() we increase the diversity of the received sequence component. For this, we have study the influence of the factor
we increase the diversity of the received sequence component. For this, we have study the influence of the factor ![]() (Equation (9)) on the performances. Figure 9 shows this influence on the performances.
(Equation (9)) on the performances. Figure 9 shows this influence on the performances.
![]() (9)
(9)
Figure 9 emphasizes the influence of values factor of the hyperbolic tangent function on the performance of SGAD. Decreasing this factor from 1 to 0.5, we can gain 1.5 dB at 10−4.
4. Conclusion
In this paper, we have proposed a new decoder based on serial GA for LDPC codes. The simulations applied on some LDPC code show that the proposed algorithm is an efficient algorithm. The comparison between our SGAD and sum-product decoder shows that our decoder is better in terms of performances. We have shown that the performances must be improved by the factor of the sigmoidal function. The obtained results will open new
![]()
Figure 5. Performance of SGAD compared to sum-product decoder for a regular LDPC (63,37) code.
![]()
Figure 6. Performance of SGAD compared to sum-product decoder for a regular LDPC (73,45) code.
![]()
Figure 7. Performance of SGAD compared to sum-product decoder for a regular LDPC (96,48) code.
![]()
Figure 8. ![]() according to r , by varying the factor ω.
according to r , by varying the factor ω.
![]()
Figure 9. Performance of SDAG decoder varying the factor values ω in the hyperbolic tangent function for LDPC (63,37) code.
horizons for the artificial intelligence algorithms in the coding theory field.