Quantum Entanglement in Coupled Lossy Waveguides Using SU(2) and SU(1, 1) Thermo-Algebras ()
1. Introduction
Recently, there has been a lot of interest in studying entanglement using coupled waveguides [1] [2] . Specially designed photonic waveguides have provided a laboratory tool for analyzing coherent quantum phenomena and have a possible application in quantum computation [3] . The entanglement between waveguide modes is at the heart of many of these experiments and has been widely studied [4] . Using coupled silica waveguides Politi et al. [5] have reported control of multiphoton entanglement directly on-chip and demonstrated integrated quantum metrology opening the way for new quantum technologies. They have been able to generate two and four photon NOON states on the chip and observe quantum interference, which further enhances the capabilities for quantum interference and quantum computing. Among various types of entangled states, NOON states are special with two orthogonal states in maximal super position thus enhancing their use in quantum information processing [6] .
For the efficient use of these waveguides in the field of quantum information, the generated entanglement should not decohere with time [7] . It is well known that the losses have a substantial effect on the wave guides; therefore, the time evolution of the entanglement has to be determined and thus it is of interest in the context of quantum information processing using lossy waveguides. The entanglement between waveguide modes and how loss affects this entanglement has recently been studied by Rai et al. [4] , by using a quantum Liouville equation. In this paper, we approach this problem from the viewpoint of thermofield dynamics [8] . This formalism has the advantage of solving the master equation for both pure and mixed states, converting thermal averages into quantum mechanical expectation values, by doubling the Hilbert space. The formalism thus makes it simpler to calculate the effects of noise and decoherence in the coupled two-mode waveguide system. We look at the effect of different type of input states and show the efficiency of the states for quantum information theory.
Thermofield Dynamics
Thermofield dynamics (TFD) [8] -[12] is a finite temperature field theory. It has been applied to many branches of high energy physics and many-body systems. TFD has been used to solve the master equation, which helps in studying the temporal evolution of entanglement. In particular, it has been used to study entanglement in the presence of a Kerr medium using an SU(1, 1) disentanglement theorem for arbitrary initial conditions by reducing it to a Schrodinger-like equation [13] [14] . Thus, all the techniques available to solve the Schrodinger equation can be used to solve the master equation. We derive the effect of losses giving rise to decoherence by solving the master equation exactly, using TFD, and then compute the decoherence and entanglement properties of some two-mode waveguide systems.
The basic formalism of TFD is as follows: corresponding to the creation and annihilation operators 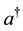 and a, which act on the physical space
and a, which act on the physical space , we introduce “thermal or tildian” operators
, we introduce “thermal or tildian” operators 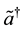 and
and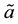 , which act on an augmented (fictitious) space
, which act on an augmented (fictitious) space 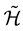 [15] -[17] . The operators a and
[15] -[17] . The operators a and 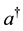 commute with
commute with 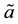 and
and 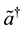 and the sets of basis vectors
and the sets of basis vectors  and
and 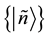 span the Hilbert spaces
span the Hilbert spaces  and
and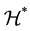 , respectively, and
, respectively, and  are the basis operators of the doubled Hilbert space, such that the identity operator is
are the basis operators of the doubled Hilbert space, such that the identity operator is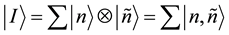 . We define a temperature dependent “thermal vacuum state”,
. We define a temperature dependent “thermal vacuum state”,
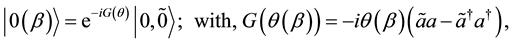 (1)
(1)
where, 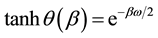 and the corresponding thermal number distribution is
and the corresponding thermal number distribution is![]() . The statistical average of any operator is equal to the vacuum expectation value of the operator with respect to the thermal vacuum. In particular, the density operator
. The statistical average of any operator is equal to the vacuum expectation value of the operator with respect to the thermal vacuum. In particular, the density operator ![]() acting on a Hilbert space
acting on a Hilbert space ![]() is a state vector
is a state vector![]() ,
,
![]() in the extended Hilbert space so that averages of operators with respect to
in the extended Hilbert space so that averages of operators with respect to ![]() acquire the properties of a scalar product.
acquire the properties of a scalar product.
![]() (2)
(2)
where the state ![]() and
and![]() . We work with the
. We work with the ![]() formalism such that
formalism such that ![]()
In TFD, the master equation is
![]() (3)
(3)
where, ![]() is a vector in the extended Hilbert space
is a vector in the extended Hilbert space ![]() and
and![]() , L is the Liouville term. Thus, the problem of solving master equation is reduced to solving a Schrodinger like equation. Symmetries associated with the Hamiltonian (such as SU(2) and SU(1, 1) symmetries) can be exploited to solve the master equation. This makes the study of entanglement in lossy systems very tractable.
, L is the Liouville term. Thus, the problem of solving master equation is reduced to solving a Schrodinger like equation. Symmetries associated with the Hamiltonian (such as SU(2) and SU(1, 1) symmetries) can be exploited to solve the master equation. This makes the study of entanglement in lossy systems very tractable.
2. Coupled Waveguide System
In optical communications, coupled waveguides are used as transmission medium. The linear coupling between two wave guides is used to transfer the power one wave guide to another. To study the decoherence and entanglement properties of the two coupled waveguides, the model of Rai and Agarwal [4] is used.
The Hamiltonian described by,
![]() (4)
(4)
where mode a corresponds to first wave guide and mode b corresponds to the second waveguide. The mode a and b obey bosonic commutation relations. The evanescent coupling in terms of distance between the two wave guide is given by J. The density operator has a time evolution given by
![]() (5)
(5)
In the presence of a damping term (system reservoir interaction), the evolution equations are governed by the Liouville equation
![]() (6)
(6)
where,
![]() (7)
(7)
where ![]() is dissipation in the material of the waveguide.
is dissipation in the material of the waveguide.
In absence of loss, the Heisenberg Equations for the field operators give their time evolution as,
![]()
To study the entanglement and decoherence properties as function of time for the coupled wave guide system, we solve the exactly master Equation (7) using TFD. This allows us to study the response to the coupling of different input states such as number, NOON and thermal states, in the coupled waveguide system. In particular, we will show that in the absence of damping, an input vacuum state evolves into a two mode SU(2) coherent state. In the presence of damping, we show that the vacuum state evolves into a two mode squeezed state and a thermal state into a thermal squeezed state.
2.1. Two Coupled Waveguides without Damping (g = 0)
The time evolution of the density operator corresponding to the two coupled waveguides without damping consisting of fields in the modes a and b from Equations (4), (5) is determined by,
![]() (8)
(8)
Now we apply the TFD-formalism (Equation (3)), by doubling the Hilbert space and get the Schrodinger type wave equation
![]() (9)
(9)
here, the Hamiltonian ![]() is given by
is given by
![]() (10)
(10)
and can be decoupled into non-tildian and tildian parts:
![]() ,
,
where,
![]() (11)
(11)
![]() (12)
(12)
Then the solution of Equation (9) is given by
![]() (13)
(13)
where, ![]() is an intial state in
is an intial state in![]() .
.
It is clear from the above that, the two Hamiltonians H and ![]() are independent. Hence, we can work with one of the Hamiltonians but since we are only interested in the physical states, we trace over the tilde states.
are independent. Hence, we can work with one of the Hamiltonians but since we are only interested in the physical states, we trace over the tilde states.
To calculate the decoherence and entanglement properties of the coupled lossy wave guide as a master Equation (8), (equivalently, the Schrodinger like Equation (9)), the underlying symmetries associated with the Hamiltonians (Equations (11), (12)) are used. To see this symmetries explicitly we define the following operators.
![]() (14)
(14)
which satisfy the SU(2) algebra,
![]() (15)
(15)
with number operator,![]() .
.
The Hamiltonian from Equation (11) in terms of the SU(2) generators is,
![]() (16)
(16)
Hence, the underlying symmetry of the Schrodinger like Equation (9) is ![]() and
and ![]() is given by
is given by
![]() (17)
(17)
Using the disentanglement formula [18] [19] , and taking the initial state ![]() as the vacuum state, the solution (17) reduces to,
as the vacuum state, the solution (17) reduces to,
![]() (18)
(18)
here, ![]()
The density matrix in the number state basis is given by
![]()
where,
![]() (19)
(19)
The entanglement properties are calculated by taking the partial transpose of ![]() and calculating the eigenvalues of the resulting matrix [20] :
and calculating the eigenvalues of the resulting matrix [20] :
![]() (20)
(20)
![]() (21)
(21)
The eigenvalues are
![]() (22)
(22)
![]() (23)
(23)
Entanglement Properties of the System
For a bipartite system, the entropy is defined as the von-Neumann entropy of the reduced density matrix traced with respect to one of the systems as
![]() (24)
(24)
such that ![]() and
and ![]() correspond to the set of eigenvalues of the reduced density operator. For the general number state, with the eigenvalues given by Equations (22), (23) the entropy is
correspond to the set of eigenvalues of the reduced density operator. For the general number state, with the eigenvalues given by Equations (22), (23) the entropy is
![]() (25)
(25)
We can also quantify the entanglement of the system by studying the time evolution for the logarithmic negativity [21] , which is an easily computable measure of distillable entanglement. For a bipartite system described by the density matrix, ![]() the log negativity is,
the log negativity is,
![]() (26)
(26)
where ![]() is the partial transpose of
is the partial transpose of ![]() and the symbol
and the symbol ![]() denotes the trace norm. Since
denotes the trace norm. Since
![]() therefore
therefore![]() . The log negativity is a non-negative quantity and a non-zero value of
. The log negativity is a non-negative quantity and a non-zero value of ![]() would mean that the state is entangled.
would mean that the state is entangled.
Now we consider various cases of optical input states.
Case-1: For two photon system as an input (i.e., N = 2):
The entropy of entanglement of the two photon input state (both ![]() and
and![]() ) is
) is
![]() (27)
(27)
which is shown in dotdashed curve of Figure 1(d). In this case, at time t = 0, we begin with a separable input state and thus the value of Entropy of entanglement (S) is zero. Then the value of “S” increases and attains a maximum value of 1.5 at Jt = 0.785212. Then decreases and eventually becomes equal to zero at Jt = 1.57061. Thus the state becomes disentangled at this point of time. At later times we see a periodic behavior and the system gets entangled and disentangled periodically. We do not see any interference effects.
Now we consider the logarithmic negativity of the various two photon states, as this is different for various two photon states, unlike the entropy.
Case-1 (a). If we take the input state as![]() , the possible output state will be
, the possible output state will be ![]() where,
where, ![]()
![]()
![]() Then we can write the log negativity entanglement of this system (from Equation (26)) as,
Then we can write the log negativity entanglement of this system (from Equation (26)) as,
![]() (28)
(28)
which is shown in thick curve of Figure 1(a). At time t = 0, we begin with a separable input state and thus the value of log negativity is zero. EN increases with time and attains a maximum value of 1.32875 for Jt = 0.42879, this is the maximally entangled state. Further, for Jt = 0.785212 we get the dips at EN = 1 (the coincidence rate of the output modes of the beam splitter will drop to zero, when the identical input photons overlap perfectly in time), due to Hong-Ou-Mandel interference [22] and for Jt = 1.57061, EN vanishes. At later times, we see a periodic behavior, attributed to the inter-waveguide coupling (J).
Case-1 (b). Now we take the input state as![]() , the possible output state will be
, the possible output state will be ![]() here,
here, ![]() ,
, ![]() ,
,![]() . The En- tanglement for this system is,
. The En- tanglement for this system is,
![]() (29)
(29)
which is shown in dotted curve of Figure 1(a). In this case, EN increases and attains a maximum value of 1.32193 at Jt = 0.785212, then decreases and eventually becomes equal to zero at Jt = 1.57061. Thus the state
becomes disentangled at this point of time. At later times we see a periodic behavior and the system gets entangled and disentangled periodically. Unlike the earlier case for the ![]() input state, we do not see any interference effects. Clearly the entanglement dynamics of the states
input state, we do not see any interference effects. Clearly the entanglement dynamics of the states ![]() and
and ![]() are different.
are different.
Case-1 (c). For two photon input NOON state: ![]() the output state will be,
the output state will be,
![]() where
where![]() ,
,
Then the logarithmic negativity of this state is
![]() (30)
(30)
which is shown in thick curve of Figure 1(c). At time t = 0, we begin with an entangled ![]() state as input and thus the value of log negativity is one. We see periodic dips due to the Hong-Ou-Mandel interference, which is characteristic of NOON states. EN increases with time and attains a maximum value of 1.32875 for Jt = 0.356988, which is the point of maximal entanglement. Further, for Jt = 0.785212, EN vanishes (we will see later that as we increase the number of photons in the NOON state, the entanglement does not vanish). At later times, we see a periodic behavior, attributed to the inter-waveguide coupling (J).
state as input and thus the value of log negativity is one. We see periodic dips due to the Hong-Ou-Mandel interference, which is characteristic of NOON states. EN increases with time and attains a maximum value of 1.32875 for Jt = 0.356988, which is the point of maximal entanglement. Further, for Jt = 0.785212, EN vanishes (we will see later that as we increase the number of photons in the NOON state, the entanglement does not vanish). At later times, we see a periodic behavior, attributed to the inter-waveguide coupling (J).
Case-2: For four photon system as an input (i.e., N = 4):
The entropy of entanglement for four photon system:
![]() (31)
(31)
This is shown in dotted curve of Figure 1(d). In this case, at time t = 0, we begin with a separable input state (Entropy of entanglement (S) = 0) after which the value of “S” increases and attains a maximum value of 2.03064 at Jt = 0.785212, it then decreases and eventually becomes equal to zero at Jt = 1.57061. Thus the state becomes disentangled at this point of time. At later times we see a periodic behavior and the system gets entangled and disentangled periodically.
Now we consider the logarithmic negativity for each of the four photon states
![]() .
.
Case-2 (a). For the input state as![]() , the possible output states are,
, the possible output states are, ![]() where,
where, ![]() , with,
, with,
![]() ,
,![]() ,
,
![]() , and
, and![]()
Then the log negativity entanglement of this system is,
![]() (32)
(32)
which is shown in thick curve of Figure 1(b). The system starts at t = 0, with a separable input state and log negativity zero, which increases at Jt = 0.200242 to EN = 1.15181 and for Jt = 0.325477 dips at EN = 1 due to Hong-Ou-Mandel interference [22] . The EN increases with time and attains a value of 1.77519 for Jt = 0.601094, this is the maximally entangled state, and for Jt = 0.785212 again we get dips at EN = 1.7277 due to Hong-Ou- Mandel interference. At later times, we see a periodic behaviorr, attributed to the inter-waveguide coupling (J). Because of involvement of four photons, we can see the double the interference effect of the two photon system.
Case-2 (b). For the input state as![]() , the possible output states are
, the possible output states are ![]() where,
where, ![]()
![]()
![]()
![]() and
and![]()
The Entanglement for this system is,
![]() (33)
(33)
which is shown in dotted curve of Figure 1(b).
Case-2 (c). Now we take the input state as![]() , the possible output state will be
, the possible output state will be
![]() here,
here, ![]()
![]()
![]()
![]() and
and![]()
The Entanglement for this system is,
![]() (34)
(34)
which is shown in thin curve of Figure 1(b).
Case-2 (d). For four photon input NOON state: ![]() the output state will be,
the output state will be,
![]() here
here![]() ,
,![]()
![]()
![]() and
and![]()
The logarithmic negativity for this system is,
![]() (35)
(35)
which is shown in dotdashed curve of Figure 1(c). In this case, unlike for the two photon NOON state, the entanglement never goes to zero. This means that increasing the number of photons in a NOON state gives a more robust entanglement which is sustained at large times. To show this we calculate the entropy for entanglement and Logarithmic negativity for a 3-photon and a five photon NOON state. The entropy of entanglement for three photon system is shown in thin curve of Figure 1(d). For three photon input NOON state the entanglement is,
![]() (36)
(36)
where, ![]()
![]()
![]()
![]() and is shown in dotted
and is shown in dotted
curve of Figure 1(c). Similarly for a five photon system as an input (i.e., N = 5): he entropy of entanglement for five photon system is, shown in thick curve of Figure 1(d).
For five photon input NOON state, the entanglement for this system is,
![]() (37)
(37)
![]()
![]()
![]()
![]()
![]()
and
![]()
The Logarithmic entropy is shown in thin curve of Figure 1(c). We see that as the photon number increases the NOON state gets more and more robust and shows that “high-noon” states can be used for more precision measurements. These results are relevant in light of the recent experimental detection of entangled 5-photon “NOON” states [23] .
2.2. Entanglement Properties for Input Thermal States
Now we consider the initial state ![]() to be the two mode thermal state. Then, in the TFD formalism, one can define the time evolved state
to be the two mode thermal state. Then, in the TFD formalism, one can define the time evolved state ![]() as
as
![]() (38)
(38)
![]() (39)
(39)
where, ![]() and
and ![]() and
and ![]() are thermal distribution functions.
are thermal distribution functions.
![]() and
and![]()
The entanglement properties are calculated by taking the partial transpose of ![]() and finding its eigenvalues
and finding its eigenvalues
![]() (40)
(40)
![]() (41)
(41)
The von-Neumann entropy of the reduced density matrix in terms of ![]() the eigenvalues of the reduced density operator is:
the eigenvalues of the reduced density operator is:
![]() (42)
(42)
Case-3 (a). For two photon system as an input (i.e., N = 2):
The entropy of entanglement for two photon is
![]() (43)
(43)
which is shown in Figures 2(a)-(c).
Case-3 (b). For four photon system as an input (i.e., N = 4):
Then the entropy of entanglement for four photon system is
![]() (44)
(44)
which is shown in Figures 2(d)-(f).
These figures show that for low values of ![]() and
and![]() , the system sustains entanglement, but as the system gets more thermalized, it decoheres and the entropy of entanglement tends to zero. The thermal effect mimics a damping effect in the system.
, the system sustains entanglement, but as the system gets more thermalized, it decoheres and the entropy of entanglement tends to zero. The thermal effect mimics a damping effect in the system.
2.3. Two Coupled Waveguides with Damping (g ¹ 0)
We consider now, losses in the coupled waveguides due to system-reservoir interaction with “g” as the rate of loss due to the material of the waveguide. The time evolution of the density operator equation is
![]() (45)
(45)
with,
![]() (46)
(46)
the following transformations,
![]() (47)
(47)
![]() (48)
(48)
gives
![]() (49)
(49)
We diagonalise this Hamiltonian by applying a squeezing (Bogolubov) transformation mixing the real and tilde fields.
![]() (50)
(50)
![]() (51)
(51)
where,
![]() (52)
(52)
![]() (53)
(53)
and ![]() and
and ![]() are the squeezing parameters and
are the squeezing parameters and ![]() and
and ![]() The final Hamiltonian is written as,
The final Hamiltonian is written as,
![]() (54)
(54)
where,
![]() (55)
(55)
![]() (56)
(56)
and![]() ,
, ![]() ,
, ![]() ,
, ![]() ; the generators of the SU(1, 1) algebra in terms of the modes A and B are given by
; the generators of the SU(1, 1) algebra in terms of the modes A and B are given by
![]() (57)
(57)
![]() (58)
(58)
and satisfy the commutation relations
![]() (59)
(59)
The Casimir operators are
![]() (60)
(60)
Then the solution of Equation (45) becomes
![]() (61)
(61)
where,
![]() (62)
(62)
By using the SU(1, 1) disentanglement formula [18] , one can write Equation (61) as,
![]() (63)
(63)
here,
![]() (64)
(64)
with
![]() (65)
(65)
subscript i labels A, B.
We consider an initial state![]() , in TFD notation. This gives us an exact solution of the density matrix:
, in TFD notation. This gives us an exact solution of the density matrix:
![]() (66)
(66)
where ![]() is an overall phase factor due to
is an overall phase factor due to ![]()
2.3.1. Calculation of Entanglement of the System for g ¹ 0
The entanglement properties are calculated by first taking trace of ![]() over the tilde space and then taking the partial transpose of
over the tilde space and then taking the partial transpose of ![]() and calculating the eigenvalues of the resulting matrix similar to the case without damping. The eigenvalues are
and calculating the eigenvalues of the resulting matrix similar to the case without damping. The eigenvalues are
![]() (67)
(67)
![]() (68)
(68)
The entropy of entanglement of the the system is
![]() (69)
(69)
Thus, for two photon state as an input state, the entropy of entanglement of the system is
![]() (70)
(70)
which is shown in thin curves of Figures 3(a)-(d).
For four photon state as an input state, the entropy of entanglement of the system,
![]()
Figure 3. The time evolution of entropy (S) for two photons (shown in thick curve) and four photons (shown in thin curve): (a) For γ = 0 (without damping); (b) For γ = 0.01; (c) For γ = 0.03; (d) For γ = 0.05, with J = 0.5.
![]() (71)
(71)
which is shown in thick curves of Figures 3(a)-(d). When ![]() goes to zero, we get the same entropy in Figure 1(d) (without damping). When we increase the value of
goes to zero, we get the same entropy in Figure 1(d) (without damping). When we increase the value of![]() , one can see the damping effect, for four photon system there is more damping than the two photon system. So, one can say that as we increase the input photons, the system will decohere more. This can also be seen by calculating the decoherence parameter.
, one can see the damping effect, for four photon system there is more damping than the two photon system. So, one can say that as we increase the input photons, the system will decohere more. This can also be seen by calculating the decoherence parameter.
Since the state is Gaussian, we can use the covariance matrix method to calculate the entanglement of the sys- tem by using Simon’s criterion [24] . The density matrix can be written as![]() , where
, where ![]() is the squeezing matrix and
is the squeezing matrix and ![]() is the rotation matrix mixing real and tilde fields. In our case, θ = 45˚ (see in Equations (47), (48)) and “r” is squeezing parameter (see in Equations (52), (53)), and
is the rotation matrix mixing real and tilde fields. In our case, θ = 45˚ (see in Equations (47), (48)) and “r” is squeezing parameter (see in Equations (52), (53)), and ![]() is the initial state of two mode system. One can clearly see that this is a product of two mode squeezed states of the four mode Hilbert space. Now we take the initial state
is the initial state of two mode system. One can clearly see that this is a product of two mode squeezed states of the four mode Hilbert space. Now we take the initial state ![]() to be the two mode vacuum state,
to be the two mode vacuum state, ![]() . To calculate the entanglement of the time evolved state
. To calculate the entanglement of the time evolved state ![]() we go over to phase space description by following transformations,
we go over to phase space description by following transformations,
![]() (72)
(72)
Then, the covariance matrix is:
![]() (73)
(73)
where, ![]() ,
, ![]() ,
,![]()
![]() .
.
Since the tildian fields are fictitious, we trace over them to get the covariance matrix for the physical modes,
![]() (74)
(74)
The canonical form of covariance matrix is given by,
![]() (75)
(75)
where,
![]() (76)
(76)
Then the separablility condition [24] for any two mode state is
![]() (77)
(77)
The symplectic eigenvalues are defined as,
![]() (78)
(78)
where,
![]()
and
![]()
The entanglement of the system is
![]() (79)
(79)
For![]() , the entanglement for two mode vacuum states without damping (i.e.,
, the entanglement for two mode vacuum states without damping (i.e.,![]() ) is shown in Fig- ure 4(a) and with damping (i.e.,
) is shown in Fig- ure 4(a) and with damping (i.e.,![]() ) is shown in Figure 4(b). We see that as damping increases the entanglement decreases, but, for low damping, the system seems to sustain entanglement to a large extent, so that it is quite robust for applications.
) is shown in Figure 4(b). We see that as damping increases the entanglement decreases, but, for low damping, the system seems to sustain entanglement to a large extent, so that it is quite robust for applications.
In order to quantify the decoherence effects, we compute ![]() as
as
![]() (80)
(80)
The behaviour of decoherence is plotted Figure 5. We have considered two cases Figure 5(a), shows the variation of decoherence with time for strong coupling for various values of ![]() and Figure 5(b), shows the evolution of decoherence with weak coupling. For strong coupling, the system decoheres in an oscillatory fashion and saturates to a non-zero value, while for weak coupling, one that for even short times, as the value of damping coefficient increases the system decoheres, to a very low value, very fast.
and Figure 5(b), shows the evolution of decoherence with weak coupling. For strong coupling, the system decoheres in an oscillatory fashion and saturates to a non-zero value, while for weak coupling, one that for even short times, as the value of damping coefficient increases the system decoheres, to a very low value, very fast.
2.3.2. Entanglement for Two Mode Thermal State with Damping g ¹ 0
Taking the initial state ![]() to be the two mode thermal vacuum state, the covariance matrix is given by,
to be the two mode thermal vacuum state, the covariance matrix is given by,
![]()
Figure 4. (a) Shows the time evolution of entanglement (EN) without damping (γ = 0); (b) Shows the time evolution of entanglement with damping (for different values of γ) with r = 0.25, J = 0.5.
![]() (81)
(81)
where,
![]() ,
,![]() ,
,![]() and
and![]() .
.
Applying Simon’s criterion Equation (77) we see that the system is entangled iff
![]() (82)
(82)
For![]() , and
, and![]() , this condition is satisfied for the values of r given in the Figure 6, in which we plot the logarithmic negativity as a function of
, this condition is satisfied for the values of r given in the Figure 6, in which we plot the logarithmic negativity as a function of![]() , for different values of r. We see that as the system not only gets less entangled for high values of γ (quantified by r), but also for large n (external heat bath). So that in the presence of a heat bath the effect of damping increases and both have to be considered when generating entanglement in the lab by using coupled cavities.
, for different values of r. We see that as the system not only gets less entangled for high values of γ (quantified by r), but also for large n (external heat bath). So that in the presence of a heat bath the effect of damping increases and both have to be considered when generating entanglement in the lab by using coupled cavities.
3. Conclusion
In this paper, we have shown that the formalism of thermofield dynamics is a powerful tool for exact studies of coupled waveguide systems. Indeed, we have exactly solved the master equation associated with SU(2) and
![]()
Figure 5. (a) Shows the time evolution of Decoherence for different values of γ with J = 3 and (b) for J = 0.25.
![]()
Figure 6. Shows entanglement (EN) vs. thermal distribution function (![]() ) for different values of r.
) for different values of r.
SU(1, 1) symmetries for coupled lossy waveguides with and without damping. For coupled waveguides without damping, special attention has been given to the time evolution of the NOON states as inputs and we have shown that as we increase the photon number, the entanglement of the NOON states survives with time, thus making them extremely suitable for quantum information. The solution for damped systems was obtained by transforming the master equation to a Schrodinger type equation and applying the disentanglement formulae for SU(2) and SU(1, 1). Our work extends that of Rai et al. [4] , as it gives the exact solution for the master equation, and, in addition shows how the entanglement behaves for input thermal states. Our results have also shown that the entanglement of the system can withstand a certain amount of damping, suggesting that it can be used for applications such as quantum computation, even if the waveguides are lossy. Furthermore, we have shown the effect of an external heat bath on the system, by applying our methods to thermal input states. Our method shows the usefulness of thermofield dynamics in quantum entanglement problems, quite orthogonal to the approach given in Ref. [25] , and allows us to handle damping in entanglement generation properties. We propose to apply this formalism to coupled light-atom systems, to shed further light on the effect of damping on the generation of entanglement.
Acknowledgements
M.N.K. wishes to acknowledge CSIR-UGC for a JRF fellowship. KVSSC acknowledges the Department of Science and technology, Govt of India, (fast track scheme (D. O. No: SR/FTP/PS-139/2012)) for financial support. We wish to thank Prof. C. Mukku and Prof. S. Chaturvedi for insightful comments. We also wish to thank V. Srinivasan for introducing us to the details of thermofield dynamics.