1. Introduction
This note is devoted to formulas for calculation of integrals over the n-dimensional hypercube centered at 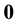
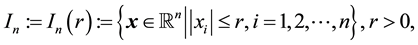
and its boundary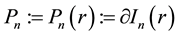 , based on integration over hyperplanar subsets of
, based on integration over hyperplanar subsets of 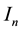 and exact for harmonic or polyharmonic functions. They are presented in Section 2 and can be considered as natural analogues on
and exact for harmonic or polyharmonic functions. They are presented in Section 2 and can be considered as natural analogues on 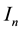 of Gauss surface and volume mean-value formulas for harmonic functions ([1] ) and Pizzetti formula [2] , ( [3] , Part IV, Ch. 3, pp. 287-288) for polyharmonic functions on the ball in Rn. Section 3 deals with the best one-sided L1-approximation by harmonic functions.
of Gauss surface and volume mean-value formulas for harmonic functions ([1] ) and Pizzetti formula [2] , ( [3] , Part IV, Ch. 3, pp. 287-288) for polyharmonic functions on the ball in Rn. Section 3 deals with the best one-sided L1-approximation by harmonic functions.
Let us remind that a real-valued function f is said to be harmonic ( polyharmonic of degree ) in a given domain
) in a given domain 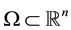 if
if 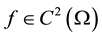
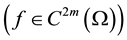 and
and 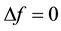
![]() on
on![]() , where
, where ![]() is the Laplace operator and
is the Laplace operator and ![]() is its m-th iterate
is its m-th iterate
![]()
For any set![]() , denote by
, denote by ![]()
![]() the linear space of all functions that are har- monic (polyharmonic of degree m) in a domain containing D. The notation
the linear space of all functions that are har- monic (polyharmonic of degree m) in a domain containing D. The notation ![]() will stand for the Lebesgue measure in
will stand for the Lebesgue measure in![]() .
.
2. Mean-Value Theorems
Let ![]() and
and ![]() be the ball and the hypersphere in
be the ball and the hypersphere in
![]() with center
with center ![]() and radius r. The following famous formulas are basic tools in harmonic function theory and state that for any function h which is harmonic on
and radius r. The following famous formulas are basic tools in harmonic function theory and state that for any function h which is harmonic on ![]() both the average over
both the average over ![]() and the average over
and the average over ![]() are equal to
are equal to![]() .
.
The surface mean-value theorem. If![]() , then
, then
![]() (1)
(1)
where ![]() is the
is the ![]() -dimensional surface measure on the hypersphere
-dimensional surface measure on the hypersphere![]() .
.
The volume mean-value theorem. If![]() , then
, then
![]() (2)
(2)
The balls are known to be the only sets in ![]() satisfying the surface or the volume mean-value theorem. This means that if
satisfying the surface or the volume mean-value theorem. This means that if ![]() is a nonvoid domain with a finite Lebesgue measure and if there exists a point
is a nonvoid domain with a finite Lebesgue measure and if there exists a point ![]()
such that ![]() for every function h which is harmonic and integrable on
for every function h which is harmonic and integrable on![]() , then
, then ![]() is an
is an
open ball centered at ![]() (see [4] ). The mean-value properties can also be reformulated in terms of quadrature domains [5] . Recall that
(see [4] ). The mean-value properties can also be reformulated in terms of quadrature domains [5] . Recall that ![]() is said to be a quadrature domain for
is said to be a quadrature domain for![]() , if
, if ![]() is a connected open set
is a connected open set
and there is a Borel measure ![]() with a compact support
with a compact support ![]() such that
such that ![]() for every
for every ![]() -
-
integrable harmonic function f on![]() . Using the concept of quadrature domains, the volume mean-value property is equivalent to the statement that any open ball in
. Using the concept of quadrature domains, the volume mean-value property is equivalent to the statement that any open ball in ![]() is a quadrature domain and the measure
is a quadrature domain and the measure ![]() is the Dirac measure supported at its center. On the other hand, no domains having “corners” are quadrature domains [6] . From this point of view, the open hypercube
is the Dirac measure supported at its center. On the other hand, no domains having “corners” are quadrature domains [6] . From this point of view, the open hypercube ![]() is not a quadrature domain. Nevertheless, it is proved in Theorem 1 below that the closed hypercube
is not a quadrature domain. Nevertheless, it is proved in Theorem 1 below that the closed hypercube ![]() is a quadrature set in an extended sense, that is, we find explicitly a measure
is a quadrature set in an extended sense, that is, we find explicitly a measure ![]() with a compact support
with a compact support ![]() having the above property with
having the above property with ![]() replaced by
replaced by ![]() but the condition
but the condition ![]() is violated exactly at the “corners” (for the existence of quadrature sets see [7] ). This property of
is violated exactly at the “corners” (for the existence of quadrature sets see [7] ). This property of ![]() is of crucial importance for the best one-sided L1-approximation with respect to
is of crucial importance for the best one-sided L1-approximation with respect to ![]() (Section 3).
(Section 3).
Let us denote by ![]() the
the ![]() -dimensional hyperplanar segments of
-dimensional hyperplanar segments of ![]() defined by
defined by
![]()
(see Figure 1). Denote also
![]()
and![]() . It can be calculated that
. It can be calculated that
![]()
and
![]()
The following holds true.
Theorem 1 If![]() , then h satisfies:
, then h satisfies:
(i) Surface mean-value formula for the hypercube
![]() (3)
(3)
(ii) Volume mean-value formula for the hypercube
![]() (4)
(4)
In particular, both surface and volume mean values of h are attained on![]() .
.
Proof. Set
![]()
and
![]()
Using the harmonicity of h, we get for ![]()
![]()
Hence, we have
![]() (5)
(5)
if ![]() and
and
![]() (6)
(6)
if![]() .
.
Clearly, (5) is equivalent to (3) and from (6) it follows
![]() (7)
(7)
which is equivalent to (4). □
Let![]() . Analogously to the proof of Theorem 1 (ii), Equation (7) is generalized to:
. Analogously to the proof of Theorem 1 (ii), Equation (7) is generalized to:
Corollary 1 If ![]() and
and ![]() is such that
is such that ![]() and
and![]() , then
, then
![]() (8)
(8)
The volume mean-value formula (2) was extended by P. Pizzetti to the following [2] [3] [8] .
The Pizzetti formula. If![]() , then
, then
![]()
Here, we present a similar formula for polyharmonic functions on the hypercube based on integration over the set![]() .
.
Theorem 2 If![]() ,
, ![]() , and
, and ![]() is such that
is such that![]() ,
, ![]() , then the following identity holds true for any
, then the following identity holds true for any![]() :
:
![]() (9)
(9)
where![]() .
.
Proof. Equation (9) is a direct consequence from (8):
![]()
3. A Relation to Best One-Sided L1-Approximation by Harmonic Functions
Theorem 1 suggests that for a certain positive cone in ![]() the set
the set ![]() is a characteristic set for the best one-sided L1-approximation with respect to
is a characteristic set for the best one-sided L1-approximation with respect to ![]() as it is explained and illustrated by the examples presented below.
as it is explained and illustrated by the examples presented below.
For a given![]() , let us introduce the following subset of
, let us introduce the following subset of![]() :
:
![]()
A harmonic function ![]() is said to be a best one-sided L1-approximant from below to f with respect to
is said to be a best one-sided L1-approximant from below to f with respect to ![]() if
if
![]()
where
![]()
Theorem 1 (ii) readily implies the following ([6] [9] ).
Theorem 3 Let ![]() and
and![]() . Assume further that the set
. Assume further that the set ![]() belongs to the zero set of the function
belongs to the zero set of the function![]() . Then
. Then ![]() is a best one-sided L1-approximant from below to f with respect to
is a best one-sided L1-approximant from below to f with respect to![]() .
.
Corollary 2 If![]() , any solution h of the problem
, any solution h of the problem
![]() (10)
(10)
is a best one-sided L1-approximant from below to f with respect to![]() .
.
Corollary 3 If![]() , where
, where ![]() and
and ![]() on
on![]() , then
, then ![]() is
is
a best one-sided L1-approximant from below to f with respect to![]() .
.
Example 1 Let![]() ,
, ![]() and
and![]() . By Corollary 2, the solution
. By Corollary 2, the solution
![]() of the interpolation problem (10) with
of the interpolation problem (10) with ![]() is a best one-sided L1-
is a best one-sided L1-
appro-ximant from below to f1 with respect to ![]() and
and![]() . Since the function
. Since the function ![]() belongs
belongs
to the positive cone of the partial differential operator ![]() (that is,
(that is,![]() ), one can compare
), one can compare
the best harmonic one-sided L1-approximation to f1 with the corresponding approximation from the linear sub- space of![]() :
:
![]()
The possibility for explicit constructions of best one-sided L1-approximants from![]() , is studied in [10] . The functions
, is studied in [10] . The functions ![]() and
and![]() , where
, where ![]() and
and ![]() are the unique best one-sided L1-approximants to f1 with respect to
are the unique best one-sided L1-approximants to f1 with respect to ![]() from below and above, respectively, play the role of basic error functions of the cano- nical one-sided L1-approximation by elements of
from below and above, respectively, play the role of basic error functions of the cano- nical one-sided L1-approximation by elements of![]() . For instance,
. For instance, ![]() can be constructed as the unique interpolant to f1 on the boundary
can be constructed as the unique interpolant to f1 on the boundary ![]() of the inscribed square and
of the inscribed square and
![]() (Figure 2).
(Figure 2).
Example 2 Let![]() ,
, ![]() and
and![]() . The solution
. The solution
![]() of (10) with
of (10) with ![]() is a best one-sided L1-approximant from
is a best one-sided L1-approximant from
below to ![]() with respect to
with respect to ![]() and
and![]() . It can also be verified that
. It can also be verified that ![]() (see Figure 3).
(see Figure 3).
Remark 1 Let ![]() is such that
is such that![]() ,
, ![]() , and
, and![]() ,
, ![]() on
on![]() . It follows from (8) that Theorem 3 also holds for the best weighted L1-approximation from below with respect to
. It follows from (8) that Theorem 3 also holds for the best weighted L1-approximation from below with respect to ![]() with weight
with weight![]() . The smoothness requirements were used for brevity and wherever possible they can be weakened in a natural way.
. The smoothness requirements were used for brevity and wherever possible they can be weakened in a natural way.