First-Principles Calculations on the Half-Metallicity of Rock-Salt Ferromagnetic FeO ()
1. Introduction
Half-metallic ferromagnets (HMFs), whose spin-polarization is theoretically ±100% at the Fermi level, are very important spintronic materials. These materials have huge application potential in spintronic devices such as magnetoresistance random access memory (MRAM), read-write magnetic head, spin transistors and magnetic sensors [1] -[3] . Furthermore, they are selected as high quality magnetic electrodes, through which the highly spin-polarized current may be injected into semiconductors. Then spintronic semiconductor devices may be manufactured [4] . FeO, as one oxide of late transition metals, is the classic example of strongly correlated materials. It is very necessary to carry on theoretical, experimental and application studies on FeO, although it is very difficult to prepare pure FeO sample due to Fe segregation [5] . Firstly, the partially filled d-shell of Fe-ions makes FeO challenging for electronic structure theory. Secondly, it is very important component of many spintronic materials prepared successfully. In 2010, magnetic nanocomposites with (NiFe2O4/CuO/FeO) crystal phases were prepared using the sol-gel method [6] . In 2011, nanoparticles composed of magnetite and wustite were successfully synthesized using the pulsed laser irradiation [7] . In 2014, FeO/Ni0.5Mn0.5Re2O4 nano-composite was prepared using glycine assisted combustion method [8] . In 2015, CoFe2O4/FeCo-FeO core-shell nanoparticles were prepared [9] . On the other hand, stoichiometric FeO had been prepared with the high pressure (similar to 5.5 GPa) by Yoshikawa et al. [10] . This shows that it is possible to prepare pure FeO with the development of experimental technique in future. Therefore, more and more attention is attracted on pure FeO or its composites, especially the first-principles calculations based on the density function theory, which are used to design new materials and calculate their physical properties including magnetic, electric and luminescent properties [11] - [14] . The geometric and electronic structures of the FeO/Pt (111) surface, and edges of FeO/Pt (111) interface were first-principles studied by Zhang et al. [11] [12] . In 2011 the ground and excited states of FeO, FeO+, and FeO− were studied by Sakellaris [13] . Screened exchange band structures for FeO were calculated by first-principles method [14] . Although many successes had been gotten about FeO and its composites, magnetic and electric properties of FeO, their micro-mechanisms are not still well understood. In this paper, the magnetic orders were studied based on the first-principles calculations.
2. Model and Calculation Method
For probing the magnetic sequence, the FeO supercell with the NaCl structure containing four Fe-ions and four O-ions was selected and shown in Figure 1(a), where these ions were signed by the corresponding element symbols. The space group was Fm3-m. The initial magnetic moment configurations of Fe-ions were set as (1) One up and three down, (2) two up and two down and (3) all up. Then their geometrical structures were optimized. The optimization was performed by the module “castep” based on density functional theory. The optimi- zation quality “fine” was elected, corresponding to the cutoff energy 340 eV and the k-point set 5 × 5 × 5. The wave functions in the software were expanded with plane-wave pseudo-potentials, and the exchange correlation functions were the Perdew-Burke-Ernzerh functions (PBE) of three nonlocal gradient-corrected exchange-cor- relations (GGA). The calculated electronic structures of the corresponding isolated atoms were Fe 3d64s2 and O 2s22p4, respectively. The minimum energy was −5205.076, −5204.952, −5205.852 eV for these three spin configurations (1), (2) and (3), respectively. This means that the ferromagnetic state, namely the spin configuration (3) is most stable for NaCl structure FeO. Therefore, the ferromagnetic state was studied in detail in this paper.
For studying magnetic and electric properties of ferromagnetic FeO, the bigger supercell containing eight Fe-ions and eight O-ions was optimized and shown in Figure 1(b). The optimized crystal constants under the ferromagnetic state are a = b = c = 0.609 nm, which are 0.97% smaller than the experimental values a = b = c = 0.615 nm. This shows that optimized results agree with experimental values. Then magnetic and electric properties of the optimized supercell were calculated in detail.
3. Results and Discussions
3.1. Total Spin-Polarized State Densities
The spin-polarized total state densities (TDOS) of ferromagnetic FeO is shown in Figure 2, where the solid and the dashed lines show the TDOS of up-spin and down-spin subbands, respectively. From Figure 2, the spin- polarization rate of FeO at the Fermi level is absolutely −100% because there are only down-spin state densities (−13.4 electrons/eV) at the Fermi level. This shows that ferromagnetic FeO is a kind of half-metallic ferromagnet. Energy areas of up-spin subbands are signed as a1 (−20.7, −18.6 eV), a2 (−8.9, −0.1 eV) and a3 (0.39, 14.8 eV), respectively. For down-spin subbands, there are four energy areas signed as b1 (−20.1, −18.1 eV), b2 (−7.8, −2.6 eV), b3 (−2.6, 3.9 eV) and b4 (3.9, 15.3 eV), respectively. Only the down-spin subband goes through the Fermi surface, so all conducted electrons are down-spin in ferromagnetic FeO. The subband a1 and b1 have certain relative energy displacement each other. However, their energy is both far smaller than the Fermi level and they have same number of electrons. Therefore, they cause no influence on magnetic and electric properties of FeO. The up-spin subband a2 and down-spin subband b2 are not axially symmetric about the horizontal x-axis, namely up-spin electrons are more than down-spin electrons. This shows that they can cause important effects on magnetic properties of materials. Down-spin subband b3 goes through the Fermi surface, which results in the conductivity and the half-metallicity of FeO. However, the subband b3 is sharp and narrow, so the conductivity of the material is very small.
3.2. Partial and Local State Densities of Ferromagnetic FeO
Partial and local state densities of ferromagnetic FeO are also calculated and shown in Figure 3 and Figure 4, respectively. Figures 3(a)-(c) correspond to the s, p and d-orbits, respectively. Figure 4(a) and Figure 4(b) correspond to one Fe-ion and O-ion, respectively. From Figure 2 to Figure 4, subbands al and b1 of TDOS are from O 2s-orbits whose energy is much lower than other orbits. Subbands a2 and b2 of TDOS are mainly from O 2p-orbits and Fe 3d-orbits. Up-spin and down-spin local densities of states (LDOS) of O-ions are not axially symmetric about the x-axis. This shows there is spin polarization in O 2p-orbits caused by the crystal field in ferromagnetic FeO. Therefore, the O-ions have some influence on the magnetic properties of FeO. On the other hand, there is evident spin polarization for 3d-robit of Fe-ions, and only down-spin state densities lie on the Fermi lever. Therefore, they cause main influence on the magnetic properties, and then the half-metallicity of ferromagnetic FeO are mainly from spin polarized Fe 3d-orbits. Furthermore, the energy of Fe 4s-orbits is
![]()
Figure 2. The spin-polarized total state densities of ferromagnetic FeO.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 3. Partial state densities of ferromagnetic FeO.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Localized state densities of ferromagnetic FeO.
evidently higher than the Fermi level. This shows that there are hybrid orbits from Fe 3d and O 2p orbits. Fe 4s electrons enter into these hybrid orbits and the electronic structure of Fe is Fe2+ 3d6.
Some calculated magnetic and electric parameters of ferromagnetic FeO are shown in Table 1. Here, parameters of only one Fe-ion and one O-ion are given in Table 1 in that all Fe-ions and O-ions have same magnetic and electric parameters based on our calculations, respectively. From Table 1, magnetic moments of one Fe-ion and one O-ion are 3.64 and 0.36 μB, respectively. The magnetic moment sum is 4.00 μB, the integer magnetic moments. This shows that ferromagnetic FeO is half-metallic ferromagnet again. On the other hand, magnetic moments of a Fe-ion are much larger than those of an O-ion. Therefore, magnetic moments of ferromagnetic FeO mainly come from Fe-ions and partially from O-ions. From the ligand field theory [14] -[16] , there are six
![]()
Table 1. Some calculated parameters of ferromagnetic FeO.
O-ligands around one Fe-ion, and then they form the coordinate compound ML6. There is strong octahedral crystal field in ML6, which results in that 3d-orbits of Fe-ions are splitted into bonding orbits containing two eg and three t
2g
-orbits with lower energy, and their corresponding anti-bonding orbits containing two 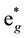 and three
and three  -orbits with higher energy. Furthermore, the energy of the eg-orbits is higher than that of the t
2g
-orbits in octahedral crystal field. Fe-ion has six 3d-electrons. Two electrons enter into eg-orbits and three electrons enter into t2g-orbits. One electron enters into one
-orbits with higher energy. Furthermore, the energy of the eg-orbits is higher than that of the t
2g
-orbits in octahedral crystal field. Fe-ion has six 3d-electrons. Two electrons enter into eg-orbits and three electrons enter into t2g-orbits. One electron enters into one 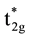 -orbits based on lowest energy principle. Therefore the electronic structure of Fe-ion is Fe2+t2g3↑eg2↑t*2g1↓.
-orbits based on lowest energy principle. Therefore the electronic structure of Fe-ion is Fe2+t2g3↑eg2↑t*2g1↓.
4. Conclusion
From our calculation, ferromagnetic FeO is a kind of half-metallic ferromagnet. Its primitive magnetic moments are 4.00 μB, which arise from spin polarization of Fe 3d-orbits. The electronic structures of Fe-ions are Fe2+t2g3↑eg2↑t*2g1↓.