Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer ()
1. Introduction
Peristalsis is a form of fluid transport induced by a progressive wave of area contraction or expansion along the walls of distensible duct containing a liquid or mixture. A peristaltic pump is a device for pumping fluids, generally from a region of lower to higher pressure, by means of a contraction wave traveling along a tube like structure. Shapiro et al. [1] explained the basic principles and brought out clearly the significances of the various parameters governing the flow. The non-Newtonian effects in peristaltic motion were included in Kaimal [2] . Later several mathematical and experimental models have been developed to understand the fluid mechanical aspects of peristaltic motion. A large body of work already exists on mathematical and experimental models containing a Newtonian or non-Newtonian fluid in a channel.
Peristalsis also have industrial and biological applications like sanitary fluid transport blood pumps in heart lungs machines and peristaltic transport of toxic liquid is used in nuclear industries. Some recent investigations made to discuss the mechanism of peristalsis include the works. Radhakrishnamacharya and Srinivasulu [3] studied the influence of wall properties on peristaltic transport with heat transfer. Mekheimer and Abd Elmaboud [4] analyzed the influence of heat transfer and magnetic field on peristaltic transport of Newtonian fluid in a vertical annulus. Hayat et al. [5] studied the effect of heat transfer on the peristaltic flow of an electrically conducting fluid in a porous space. Krishna Kumari et al. [6] studied the peristaltic pumping of a magnetohydrodynamic Casson fluid in an inclined channel. Ravi Kumar et al. [7] considered power-law fluid in the study of peristaltic transport.
The effect of porous medium on the motion of the fluid has been studied by many authors. Elshehawey et al. [8] studied the effect of porous medium on peristaltic motion of a Newtonian fluid. Eldabe [9] studied magnetohydrodynamic flow through a porous medium fluid at a rear stagnation point. Eldabe et al. [8] studied MHD flow and heat transfer in a viscoelastic incompressible fluid confined between a horizontal stretching sheet and a parallel porous wall. Elshehawey et al. [9] studied the peristaltic motion of a Generalized Newtonian fluid through a porous medium. El-Dabe et al. [10] studied the magnetohydrodynamic flow and heat transfer for a peristaltic motion of Carreau fluid through a porous medium.
The study of the influence of mass and heat transfer on Newtonian and non-Newtonian fluids has become important in the last few years. This importance is due to a number of industrial processes. Examples are food-processing, biochemical operations and transport in polymers. Eldabe et al. [11] studied the heat and mass transfer in hydromagnetic flow of the non-Newtonian fluid with heat source over an accelerating surface through a porous medium. Srinivas and Kothandapani [12] dealt with peristalsis and heat transfer. Hayat et al. [13] - [15] analyzed the peristaltic mechanism with heat transfer. Eldabe et al. [16] studied the effect of couple stresses on the MHD of a non-Newtonian unsteady flow between two parallel porous plates. The main aim of this study is to investigate the problem of the peristaltic flow of a conducting Sisko fluid in a porous channel with heat and mass transfer; the system of non-linear partial differential equations which describe this motion with heat and mass transfer subjected to the appropriate boundary conditions is solved analytically by using perturbation method. The expressions of the velocity, the temperature and the concentration are determined. The effects of different parameters on these expressions are discussed through graphs.
2. Basic Equations
The basic equations governing the flow of an incompressible fluid are expressed as follows:
The continuity equation
 (1)
(1)
The momentum equation
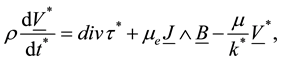 (2)
(2)
where 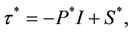 and
and
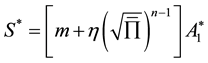 , (3)
, (3)
where  and
and 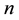 are the material parameters of the fluid. Note that for
are the material parameters of the fluid. Note that for 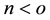 the fluid describes shear thinning, for
the fluid describes shear thinning, for 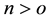 the fluid describes shear thicking, for
the fluid describes shear thicking, for 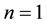 the Newtonian fluid is recovered and for
the Newtonian fluid is recovered and for  the generalized power-law model can be obtained.
the generalized power-law model can be obtained.
The temperature equation
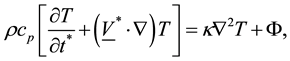 (4)
(4)
The concentration equation
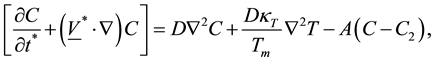 (5)
(5)
The dissipation function 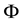
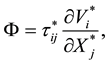 (6)
(6)
Maxwell s equations
 (7)
(7)
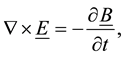
![]()
Ohm’s equation
![]() (8)
(8)
where ![]() is the velocity vector,
is the velocity vector, ![]() is the density,
is the density, ![]() is the material time derivative,
is the material time derivative, ![]() is the permea-
is the permea-
bility, ![]() is the current density,
is the current density, ![]() is the electrical conductivity,
is the electrical conductivity, ![]() is the magnetic permeability,
is the magnetic permeability, ![]()
is the electric field and ![]() is the Cauchy stress, T and C are temperature and concentration of the fluid,
is the Cauchy stress, T and C are temperature and concentration of the fluid, ![]() is the thermal conductivity,
is the thermal conductivity, ![]() is the specific heat capacity at constant pressure, D is the coefficient of mass diffusivity,
is the specific heat capacity at constant pressure, D is the coefficient of mass diffusivity, ![]() is the thermal diffusion ratio,
is the thermal diffusion ratio, ![]() is the mean fluid temperature and A is the reaction rate constant.
is the mean fluid temperature and A is the reaction rate constant.
3. Mathematical Formulation
Consider the two-dimensional motion of an incompressible Sisko fluid in an infinite channel of width![]() , see Figure 1. In the upper wall we assume an infinite sinusoidal wave train moving ahead with constant velocity c along it while the lower plate is fixed at
, see Figure 1. In the upper wall we assume an infinite sinusoidal wave train moving ahead with constant velocity c along it while the lower plate is fixed at![]() . The wavy surface is defined as
. The wavy surface is defined as
![]() (9)
(9)
where b is the wave amplitude, ![]() is the wave length and
is the wave length and ![]() is the time.
is the time.
Now, Equations (2)-(6) can be written in two-dimensional ![]() as follows:
as follows:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
where
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Subjected to the following appropriate boundary conditions:
![]() (19)
(19)
Choose the wave frame ![]() moving with speed c, where
moving with speed c, where
![]() (20)
(20)
In which ![]() are components of the velocity in the moving coordinates system.
are components of the velocity in the moving coordinates system.
Then, the Equations (10)-(19) can be written as:
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
where
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
The boundary conditions are:
![]() (29)
(29)
In order to simplify the governing equations of the motion, we may introduce the following dimensionless transformations:
![]() (30)
(30)
where, ![]() and
and ![]() are the temperature and the concentration of the fluid at the lower wall of the channel,
are the temperature and the concentration of the fluid at the lower wall of the channel, ![]() and
and ![]() are the temperature and the concentration of the fluid at the upper wall of the channel.
are the temperature and the concentration of the fluid at the upper wall of the channel.
Substituting (30) into Equations (21)-(29) we obtain the following non-dimensional equations after dropping the star mark:
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
The boundary conditions are:
![]() (39)
(39)
where, the dimensionless parameters are defined by:
![]() is the Wave number,
is the Wave number, ![]() is the Reynolds number,
is the Reynolds number, ![]() is the Darcy number,
is the Darcy number, ![]() is the Magnetic field parameter,
is the Magnetic field parameter, ![]() is the Non-Newtonian parameter,
is the Non-Newtonian parameter, ![]() is the Prandtle number,
is the Prandtle number, ![]() is the Eckert number,
is the Eckert number, ![]() is the Schmidt number,
is the Schmidt number, ![]() is the Soret number and
is the Soret number and ![]() is the chemical reaction parameter.
is the chemical reaction parameter.
By using the following definition of stream function ![]() as:
as:
![]() (40)
(40)
The system of Equations (3.30)-(3.38) can be written as:
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
The boundary conditions for the dimensionless stream function in the moving frame are given by:
![]() (47)
(47)
The dimensionless form of the surface of the peristaltic wall can be written as:
![]()
where ![]() is the amplitude ratio or the occlusion. and
is the amplitude ratio or the occlusion. and
![]() is the total flux number (48)
is the total flux number (48)
4. Solution of the Problem
According to long wavelength approximation ![]() [1] , Equations (41)-(46) after eliminating the pressure gradient become:
[1] , Equations (41)-(46) after eliminating the pressure gradient become:
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
In order to solve the Equations (49)-(51) subjected to the boundary conditions, we suppose the following perturbation for small non-Newtonian parameter![]() :
:
![]() (55)
(55)
Substituting (55) into (49)-(54) and comparing the coefficient of zero and first order of ![]() we get.
we get.
4.1. Zero Order System of h
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
With the respective boundary conditions
![]() (59)
(59)
4.2. First Order System of h
We shall consider the case of Dielatent fluids when n > 1, and we choose (n = 3), then we have the following system of first order of ![]()
![]() (60)
(60)
![]() (61)
(61)
![]() (62)
(62)
with the respective boundary conditions
![]() (63)
(63)
4.3. Solution for System of Zero Order
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
4.4. Solution for System of First Order
![]() (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
5. Results and Discussions
The problem of the peristaltic flow of a Sisko fluid through a porous medium with heat and mass transfer has been discussed. The effects of non-Newtonian dissipation and chemical reaction on the fluid flow have been considered. We obtained the solutions of the momentum, heat and mass equations analytically by using the perturbation technique for small non-Newtonian parameter ![]() after considering the long wave approximations.
after considering the long wave approximations.
Figure 2 illustrates the relation between the value of stream function ![]() and the magnetic parameter
and the magnetic parameter![]() , it is clear that
, it is clear that ![]() increases with increasing the magnetic parameter, while it decreases with increasing the permeability parameter
increases with increasing the magnetic parameter, while it decreases with increasing the permeability parameter ![]() which seen through Figure 3.
which seen through Figure 3.
In Figure 4, the relation between the value of stream function ![]() and the amplitude ratio
and the amplitude ratio ![]() has been illustrated. it is clear that
has been illustrated. it is clear that ![]() decreases with the decrease of
decreases with the decrease of![]() .
.
Figure 5, illustrates the relation between the value of temperature ![]() and the magnetic parameter
and the magnetic parameter![]() , it is clear that increases with increasing the magnetic parameter.
, it is clear that increases with increasing the magnetic parameter.
In Figure 6, we can observe that the value of temperature increases with increasing the Prandtle number parameter![]() , while in Figure 7, the relation between the value of temperature
, while in Figure 7, the relation between the value of temperature ![]() and the Eckert number
and the Eckert number ![]() has been illustrated. It is clear that
has been illustrated. It is clear that ![]() increases with the increase of
increases with the increase of![]() .
.
![]()
Figure 2. Stream function profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 3. Stream function profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 4. Stream function profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 5. Temperature profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 6. Temperature profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 7. Temperature profiles ![]() for some values of
for some values of![]() .
.
In Figure 8, the relation between the value of concentration ![]() and the magnetic parameter
and the magnetic parameter![]() , it is clear that
, it is clear that ![]() decreases with increasing the magnetic parameter. But we can observe from Figure 9 that
decreases with increasing the magnetic parameter. But we can observe from Figure 9 that ![]() decreases with increasing the Schmidt parameter
decreases with increasing the Schmidt parameter![]() , also in Figure 10, the relation between the value of concentration function
, also in Figure 10, the relation between the value of concentration function ![]() and the Soret value
and the Soret value ![]() has been illustrated. It is clear that
has been illustrated. It is clear that ![]() increases with the increase of
increases with the increase of ![]() as in Figure 11.
as in Figure 11.
6. Conclusion and Applications
In this work, we study the peristaltic motion of magneto-hydrodynamics flow with heat and mass transfer for incompressible non-Newtonian fluid through a porous medium. The governing partial differential equations of this problem, subjected to the boundary conditions are solved analytically by using perturbation technique. The
![]()
Figure 8. Concentration profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 9. Concentration profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 10. Concentration profiles ![]() for some values of
for some values of![]() .
.
![]()
Figure 11. Concentration profiles ![]() for some values of
for some values of![]() .
.
analytical forms for the stream distribution![]() , the temperature
, the temperature ![]() and the concentration
and the concentration ![]() are obtained. The effects of various physical parameters of the problem on these formulas are discussed and have been shown graphically. It is seen that the
are obtained. The effects of various physical parameters of the problem on these formulas are discussed and have been shown graphically. It is seen that the ![]() increases with increasing the magnetic parameter
increases with increasing the magnetic parameter![]() , while it decreases with increasing the permeability parameter
, while it decreases with increasing the permeability parameter![]() . Also it is clear that
. Also it is clear that ![]() increases with the increase of
increases with the increase of![]() ,
,
The study of this phenomenon is very important, because the study of flow through porous medium has many applications. It has an important role in agricultural, extracting pure petrol from crude oil and chemical engineering. There are examples of natural porous media such as wood, filter paper, cotton, leather and plastics. As a good biological example on the porous medium, the human lung galls bladder and the walls of vessels. The peristaltic motion has been found to involve in many biological organs such as esophagus, small and large intestine, stomach, the human ureter, lymphatic vessels and small blood vessels. Also, peristaltic transport occurs in many practical applications involving biomechanical systems such as finger pumps.
Appendix
![]()
![]()
![]()
![]()
![]()
![]()