New Localization Technique for Mobile Wireless Sensor Networks Using Sectorized Antenna ()
1. Introduction
Mobile wireless sensor networks (MWSNs) are a particular class of wireless sensor network (WSN) in which mobility plays a key role in the execution of the application. In recent years, mobility has become an important area of research for the WSN community. Although WSN deployments were never envisioned to be fully static, mobility was initially regarded as having several challenges that needed to be overcome, including connectivity, coverage, and energy consumption, among others. However, recent studies have been showing mobility in a more favorable light [1] . Rather than complicating these issues, it has been demonstrated that the introduction of mobile entities can resolve some of these problems [2] . One of the most significant challenges for MWSNs is the need for localization. In order to understand sensor data in a spatial context, or for proper navigation throughout a sensing region, sensor position must be known. Because sensor nodes may be deployed dynamically, or may change their positions during run-time, there may be no way of knowing the exact location of each sensor node at any given time. On the other hand, mobile sensors must frequently estimate their positions, which take time and energy, and consume other resources needed by the sensing application. Furthermore, localization schemes that provide high-accuracy positioning information in WSNs cannot be employed by mobile sensors, because they typically require centralized processing, take too long to run, or make assumptions about the environment or network topology that do not apply to dynamic networks.
There are three visible advantages of knowing the location information of sensor nodes. First, location information is needed to identify the location of an event of interest. For instance, the location of an intruder, the location of a fire, or the location of enemy tanks in a battlefield is of critical importance for deploying rescue and relief troops. Second, location awareness facilitates numerous application services, such as location directory services that provide doctors with the information of nearby medical equipment and personnel in a smart hospital, target-tracking applications for locating survivors in debris, or enemy tanks in a battlefield. Third, location information can assist in various system functionalities, such as geographical routing [3] - [10] , network coverage, network routing, perimeter finding, and topology checking [11] - [21] , and location-based information querying [22] . Hence, with these advantages and much more, it is natural for location-aware sensor devices to become the defector standard in WSNs in all application domains that provide location-based service.
Recently some localization techniques have been proposed to allow sensor nodes to estimate their locations using information transmitted by a set of seeds that know their own locations (for example, the seeds can have GPS receivers). They all suffer from one or both of the following problems: 1) Dependence on special hardware: Techniques that depend on measuring ranging information from signal strength [23] , the time of arrival [24] , time difference of arrival [25] , and angle of arrival [26] require hardware that is typically not available on sensor nodes. Adding the required hardware increases the cost and size of the sensor nodes; 2) Requirement for particular network topologies: Most techniques require seed nodes to be numerous and evenly distributed so they can cover the whole network. But prior deployment of seeds is not possible in many sensor network applications (for example, sensor nodes drop from plane over a hostile territory). Hop count based techniques [27] [28] avoid the need for a large number of seeds, but instead require dense and uniform node distribution
In this paper, we propose a new distributed range free technique to localize sensor nodes with the help of seeds that attached with sectorized antenna. The seeds enable the sensor node with unknown location to know the sector that it locates with respect to neighbor seeds. The location can be obtained by calculating the area of intersection of the sectors and calculate the centroid of this area (node location). Our proposed technique has the following advantages: 1) It does not require special hardware except some beacon seeds, 2) It works in a very low seed density which is really cost effective, 3) It does not require particular network topologies, and 4) It increases the accuracy of the location by decreasing the expected location area.
The rest of the paper is organized as follows: Section 2 briefly discusses the related of existing localization approaches to our proposed technique. Section 3 presents information regarding the sectorized antenna systems. Section 4 describes the details of the proposed technique. In Section 5, simulation results are reported and a comparative study of the localization performance is conducted. Finally, Section 6 concludes our work.
2. Related Work
Extensive research has been done on localization for WSNs. Some general surveys can be found in [29] - [31] . The approaches taken to achieve localization in WSNs differ in their assumptions about the network deployment and the hardware’s capabilities. There are many proposed techniques in the literature for static and mobile WSNs.
Centralized localization techniques depend on sensor nodes transmitting data to a central location, where computation is performed to determine the location of each sensor node [32] . Distributed localization methods do not require centralized computation, and rely on each sensor node to determine its location with only limited communication with nearby nodes. These methods can be classified as range-based and range-free.
Range-based techniques use distance estimates or angle estimates in location calculations, while a range-free solution depends only on the contents of received messages. Many range-based techniques are developed based on using special hardware to estimate time of arrival [33] , received signal strength [23] [34] time difference of arrival of two different signals (TDOA) [35] , and angle of arrival (AOA) [25] . Though they can reach fine resolution, either the required hardware is expensive (ultrasound device for TDOA, antenna arrays for AOA) or the results depend on other unrealistic assumptions about signal propagation (for example, the actual received signal strengths of radio signals can vary when the surrounding environment changes).
As opposed to range-based methods, range-free ones only use the content of messages received from neighbor sensor nodes, in order to estimate their locations. DV-Hop in [36] is a range-free version of APS in which nodes propagate hop count distance to landmarks. The idea of DV-Hop has been used by several other schemes, such as the amorphous localization algorithm [37] and the Probability Grid [38] . These schemes waste the time and the energy of the sensor nodes by the propagation of hop count distance to landmarks and the hop count distance requires the path between the landmarks and the sensor node to be direct which do not simulate the real condition (zigzag path). Two more range-free schemes are the Centroid method [39] , where each sensor node estimates its location by calculating the center of the locations of the landmarks it hears, and the APIT method [40] , it divides the deployment area in triangular regions between landmarks, and uses a grid algorithm to estimate the largest area in which a sensor node is likely to be found. The work in [39] [40] requires a special density and deployment of reference nodes. In [39] , the sensor node cannot determine the direction of itself with respect to the landmarks so more than one node can share the same location because of the hearing of the same landmarks as shown in Figure 1. In [40] , a signal strength measurement is required for PIT test.
To reduce the total costs in terms of needed hardware and deployment effort, a number of papers had been proposed using mobile anchors to help in localizing nodes [41] -[44] . A mobile anchor performs the same task as a static anchor broadcasting its accurate location but can take the form of a human-carried PDA or a robot. The anchor in motion improves the accuracy in resource-poor networks where typically few anchors are available. By letting an anchor moves, the percentage of nodes receiving anchor messages usually increases. A mobile anchor therefore represents many virtual static anchors. In [45] , to determine the best path, an anchor has to follow to maximize the improvement in location-estimation accuracy. In this paper, in addition to the mobility of sensor nodes, the seeds are moving uncontrollably all the time. We do not require special hardware to estimate time of arrival, received signal strength, time difference of arrival of two different signals (TDOA), or angle of arrival (AOA), also we neither require nodes or seeds to be manually deployed in special position nor a special density of seeds because we use the help of sensor nodes that recently computed their positions.
Several protocols have been proposed for MWSNs [46] - [50] . In [46] , MCL is designed for MWSNs based on the sequential Monte Carlo method. The key idea of the sequential Monte Carlo Localization is to represent the posterior distribution of sensor nodes possible locations using a set of weighted samples. Localization happens
![]()
Figure 1. S1, S2 and S3 have the same locations.
in two steps. First, the prediction step leads to choosing a set of samples representing the belief of the node regarding its location. During the prediction step, a sensor node picks random locations within the deployment area, possibly constrained by its maximum speed and the previous location samples. Second, the filtering step aims at removing the impossible locations from the set of samples. The filtering is done using information obtained from the environment, such as the location of the anchors in the case of a sensor node or the detection of landmarks in the case of a mobile robot. The process will be repeated and the sensor or robot is able to update its position estimation. The accuracy of MCL depends on the speeds of the seeds and nodes. A range-based version of MCL has also been proposed [47] , which combines range-based and range-free location information to reduce the estimation error. In [48] , Baggio et al. improved the MCL scheme by reducing the sample prediction area. Their work, called MCB, draws valid samples faster and reduces the number of iterations necessary to fill the sample set. Computation overhead is reduced by this mechanism, but it still depends on specific parameters such as the fixed radio transmission range. The original MCL algorithm uses information about one-hop and two-hop anchors at filtering time only, for rejecting impossible samples. In MCB, the information about the anchors heard to constrain the area from which the samples are drawn. In [49] , Hsieh et al. proposed a localization algorithm which dynamically updates and makes use of reference information for cost-efficiency, and has a feasible solution for nodes receiving insufficient anchor information. In [50] , the authors proposed a coordinated localization algorithm for MWSNs with camera sensors to operate under global positioning system (GPS) denied areas or indoor environments. In this paper, we use the sectorized antenna that can determine the direction of the node, improve the communication, and conserve the energy. We determine the smallest region that the node is expected to be there by computing the intersection of the sectors. We benefit from the cooperation between seeds and neighbor sensor nodes that achieved high localization performance. Our seeds are moving uncontrollably all the time and our scheme can be executed with a low density of seeds. The sensor information is used to reduce even more the prediction area, thus reducing the estimation error of the non-seed nodes. Our scheme belongs to the range-free category of localization algorithms.
3. Sectorized Antenna Systems
The main function of the used antennas in any communication system is to compensate for the loss of signal strength that occurs when a signal is transmitted from the source to the destination (and vice versa). Most antennas are resonant devices, which operate efficiently over a relatively narrow frequency band. An antenna must be tuned to the same frequency band that the radio system to which it is connected operates in, otherwise reception and/or transmission is impaired. Physical designs of antenna can vary greatly. Sectorized antenna systems take a traditional cellular area and operationally each sector is treated as a different cell. Sectorized antennas increase the possible reuse of a frequency channel in such cellular systems by reducing potential interference across theoriginal cell, and they are widely used for this purpose. Six sectors per cell have been used in practical service. When combining more than one of these directional antennas, the base station can cover all directions [51] .
In our work, we assume that each seed is attached with sectorized antenna to make the sensor of unknown location aware of the sector it locates with respect to other known location sensors. These antenna systems are extensively used in cellular systems where a base station divides the traditional cellular area into independent sectors, and each of these sectors treated as a sub-cell. By using sectorized antennas, the range of each sector is increased. Also, sectorized antennas increase the possibility of channel reuse and reduce the interference. We use sectorized antennas in the localization to reduce the intersection area of transmission ranges by calculating the intersections of the transmission range sectors. So the diameter of the estimated area in which a node resides can be reduced, this provides a good location estimate.
4. Localization Algorithm
In this section, we introduce our proposed technique for mobile sensors localization, where we consider a network in which a small fraction of seeds are equipped with hardware, e.g., GPSs, which allow them to know their locations all times; all other sensors are identical. Our protocol can handle heterogeneity in radio range, but for ease of exposition, we assume that each sensor node has the same ideal radio range r. We assume that sensor nodes are equipped with omnidirectional antennas and transmit with a power Pn, while Seeds are equipped with M directional antennas with a directivity gain G > 1, and can transmit with a power Ps > Pn. In MWSN, every sensor node knows whether other sensor node is in its transmission range by broadcasting a message to its one-hop neighbors and check the feedback (if one node is in the transmission range of other, the distance between them will not exceed the transmission range r), this can naturally offer static constraint obtained from transmission range.
We assume that the time is divided into discrete time units. Since a node may move away from its previous location, it needs to determine its location in each time unit. The mobility provides a special feature of MWSN: velocity constraint. For example, we assume that every sensor node can move within a maximum distance Vmax at one time slot, so the new location of the sensor node cannot be out of the circle that has last location as center and radius Vmax (see Figure 2).
In the time duration between two consecutive localization points, the error in the estimate of the location increases as the sensor node moves (on average) increasingly further from its last location estimate. In order to control this error, localization must be repeated with enough frequency to ensure that the estimated location meets some application-level error requirements (e.g., the estimate remains within a pre-specified threshold from the actual location). However, carrying out localization with high frequency drains the node’s energy. Solutions to this problem must balance the need to bound error with the cost of carrying out localization. Note that dynamic control of localization is needed whether localization is carried out on demand (i.e., the node queries neighbors or fixed localization nodes for localization information) or proactively (e.g., by having localization nodes periodically transmit localization beacons, or using GPS). We can assume that the time duration between two consecutive localization points can be determined by the node using the proposed protocols in [52] based on the proposed application. The main localization process is divided into three phases: initialization, predicting localization, and filtering the prediction.
Initialization phase: In initialization phase, the sensors and the seeds are randomly distributed in the deployment region with density ρn and ρs. Sensor nodes and the seeds are allowed to move freely within the deploymentarea A.
Prediction phase: In prediction phase, the localization of the unknown sensor node v at time t is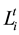 , as a result, the sensor node v must be in the circle whose center is
, as a result, the sensor node v must be in the circle whose center is 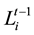 and radius is Vmax.
and radius is Vmax.
Filtering phase: In filtering phase, the node filters the impossible localizations based on observations information. We assume that time is discrete and all messages are received instantly. Hence, at time t, every node within sector area of a seed will hear localization information from that seed. This phase is composed of two steps: in the first step, the sensor node discovers the neighbors which know their locations (the neighbors can be seeds or nodes that recently calculated their locations with the help of seeds to increase the confidence of location computation), and in the second step, the sensor node determines the expected area by calculating the area of intersections of Vmax circle and the neighbors transmission range sectors that the sensor node locates inside (as shown in Figure 3). The accuracy of the localization increases as the sector angle decreases (will be covered in
![]()
Figure 2. The dashed area is the intersection area of sectors and Vmax circle location determination.
![]()
Figure 3. The dashed area is the intersection area of sectors and Vmax circle.
the next subsection).
To allow sensor nodes to re-estimate their location, seeds need to periodically broadcast new beacons with their coordinates and sector information. Sensors determine their location based on the beacon information transmitted by the seeds and the neighbor sensor nodes, which recently computed their locations. Each seed transmits different beacons at each antenna sector. Each beacon contains:
1) Locator’s coordinates, and
2) Angles of the antenna boundary lines with respect to a common global axis.
If a sensor node receives a beacon transmitted at a specific antenna sector of a seed Si, it has to be included within that sector.
Given the communication range r, the coordinates of the transmitting locators, and the sector boundary lines provided by the beacons, each sensor node determines its location as the center of gravity (CoG) of the overlapping region of the different sectors. The CoG is the least square error solution given that a sensor node can lie with equal probability at any point in the overlapping region.
The sensor node determines a search area where it will attempt to locate itself inside a circle with previous node’s location as center and Vmax as radius. Sensor node places points of equally spaced within the circular search area. Initially, all the points have a zero score. If a point is included in a sector the sensor node increments its score by one. Otherwise, no change in its score. Let the coordinates of a point g be denoted as (xg,yg), point g is included in a sector originating from seed if it satisfies two conditions:
1) g has to lie within the communication range of a seed (locator).
2) The angle of the line connecting seed’s location and g has to lie within the sector.
In this case, the number of seeds that heard by the sensor must be at least two. If it is the first time for the sensor node to determine its location, the sensor node computes a search area as rectangular search area with corners of the minimum Xmin, Ymin and maximum Xmax, Ymax seeds coordinates that it can hear. If there is only one seed heard the searched area will be its communication circle.
The sensor node determines its location as the centroid of all the points that define the overlapping region:
 (1)
(1)
where n is the number of points of the overlapping region, and (xpi, ypi) are the coordinates of the points.
Algorithm outlines
Every sensor node that wants to estimate its location in the MWSN will execute the following steps:
1) At every time slot, send a request message to every neighbor sensor node in your transmission range asking for location and the sector’s angle from which it received the message (see Figure 3).
2) Up on the reception of reply messages from neighbor sensor nodes and up on hearing the beacons transmitted by the seeds. The sensor node will extract the following information from every message:
a) The angle of the antenna boundary lines with respect to a common global axis (from seed).
b) The location of the neighbor (seed or non-seed node).
c) The accuracy degree if the message received from a non-seed node.
3) If the number of seeds is not enough, include the locations of non-seed nodes with high accuracy degree.
4) Determine the intersection area of the sectors and the circle of previous node’s location as center and Vmax as radius (if it is not the first time to be localized) and the located neighbor sensor nodes’ communication circles (see Figure 3).
5) Compute the estimated location by taking the centroid or the center of gravity (COG)(average of X coordinates and Y coordinates of the overlapped points with high score) of the area (COG of polygon).
6) If you receive a request message, and you are not a seed, reply with your location and the accuracy degree (the number of seeds that you are used to localize yourself). The sensor nodes with high accuracy degree will be used for the new localization.
In this protocol, each sensor node that wants to relocate itself discovers its communication neighbor sensor nodes by sending its location information along with its ID to its neighbors. If n is the total number of nodes in the network and Navg is the average neighbors of each sensor node, therefore, the total number of exchanged messages for each time slot will be n * Navg.
5. Simulation Results
The key metric for evaluating a localization technique is the accuracy of the location estimates versus the communication and deployment costs. In general, increasing the density of seeds or the frequency of location announcements should improve accuracy. In this section, we evaluate the proposed technique by measuring how its estimated location errors vary with various network and algorithm parameters. In addition, we compare our results with existing localization techniques, namely Centroid [32] and MCL [46] techniques described in Section 2. Our simulation experiments were conducted using ns2. Experimental results are the average of 10 executions with different pseudorandom number generator seeds.
In our experiments, we vary parameters of both the sensor network and sensor nodes, and the proposed technique. For all of our experiments, sensor nodes are randomly distributed in an obstacle-free region of 200 m × 200 m rectangular region. We assume a fixed transmission range, r, of 50 m for both nodes and seeds and the sectorized antenna’s angle is 90˚. The network and node parameters we vary are: Speed of the sensor nodes and seeds. We represent the speed as the moving distance per time unit. A node’s speed and seed’s speed are randomly chosen. We consider the impact of speeds, node density, and the Sectorized antenna’s angle on accuracy.
In our experiments, we characterize the accuracy of the estimate by the following defined localization error LE:

where (xest,yest) is the estimation position and (xa,ya) is the actual position.Unlike the proposed technique, the Centroid localization techniques do not exploit past information, so it does not improve over the time. Figure 4 shows the comparison of the localization error between the proposed and the Centroid techniques (distance between the actual position and the estimated one of 80 unknown nodes). The accuracy of the proposed technique improves quickly.
Increasing the density of seeds makes localization easier, but increases network and deployment costs. Figure 5 shows the impact of seeds density on the estimated error in case of the proposed, the centroid, and MCL techniques. As shown in the figure, the performance of the Centroid and MCL techniques are clearly improved as the number of seeds increases however, the performance of the proposed technique is a little affected by the increasing of the seeds number and this is because our technique does not depend only on the number of seeds but also on the number of non-seed nodes that have high accuracy localization.
Figure 6 shows the impact of nodes density on the estimated error in case of the proposed and Centroid techniques. From the figure, both techniques are little affected by nodes density, however our proposed technique requires a threshold node density in order for requesting node to receive location information from enough neighbors. Figure 7 shows the impact of sectorized antenna’s angle on the localization error in our proposed
![]()
Figure 4. The error comparison between the proposed and the Centroid techniques (Vmax = smax = r).
![]()
Figure 5. The impact of seeds density on the Estimated Error in case of the proposed, the centroid, and MCL techniques (Vmax = smax = r).
technique. From the figure, the localization error will be decreased as the Sectorized antenna’s angledecreases and this is because as the sector angle decreases the intersection area of the sectors will be reduced and then it will reduce the estimated error.
Node speed impacts the localization process in two ways. The increased speed makes the predicted locations less accurate since the next possible locations fall into a larger region. On the other hand, faster movement leads to more new observations in each time step, and hence more impossible locations can be filtered. Varying node
![]()
Figure 6. The impact of nodes density on the Estimated Error in case of the proposed and Centroid techniques (Vmax = smax = r).
![]()
Figure 7. The Impact of Sectorized antenna’s angle on the estimated error of the proposed technique (Vmax = smax = r).
speed is similar to varying the time between location announcements. If announcements are more frequent, localization is more accurate but communication overhead increases. We measure maximum node speed as Vmax and distribute actual node speeds between 0 and Vmax [53] . Figure 8 shows the impact of node speed on the converged localization error as the distance travelled per announcement time unit increases from 0.1 r to 2 r in the proposed and MCL techniques. In MCL, the error is least when nodes are slowest, and then increases gradually as node speed increases. At slow speeds, sensor nodes are thus more often producing location estimates without being able to use beacon locations. This increases the inaccuracy of the set of samples over time. In the worst
![]()
Figure 8. The Impact of node speed on the estimated error in case of the proposed and MCL techniques).
case, sensor nodes are localized in the middle of the deployment area if no valid sample can be drawn once a beacon is heard again.
For larger values of Vmax, such as 0.8 r and above, the motion of the sensor nodes allows them to hear beacons more often and this limits the decay of the sample set. However, since the distance a sensor node can travel in a time unit is larger, the area from which the random samples are drawn also increases. This affects the accuracy in a negative way. The behavior of our algorithm is not as dramatically affected by the maximum node speed as it is the case with MCL. This is because the prediction area is not affected by large value of Vmax so much as MCL.
6. Conclusion and Future Work
Many wireless sensor network applications depend on nodes being able to accurately determine their locations. With the limitation of sensor capability, we proposed a range-free solution to localize mobile sensor nodes using sectorized antenna for the scenario that both sensor nodes and seeds move uncontrollably. The core observation of our work is the usage of sector information as the estimation of the node’s orientation. All the previous techniques use only neighbor seeds’ locations in their computations that need a special density, which is not the case in our proposed technique where the high accuracy locations of the nodes that are recently computed can be used to help their neighbor nodes to compute their locations. Our simulation experiments reveal that our proposed technique can provide accurate localization better than the existing techniques even when the seed density is low. Many issues remain to be explored in future work including how well our assumptions hold in different mobile sensor network applications, how different types of motion affect localization, and how our technique can be extended to provide security.