Selection for Eldana saccharina Borer Resistance in Early Stages of Sugarcane Breeding in South Africa ()
1. Introduction
Eldana saccharina (eldana) is an indigenous lepidopteran insect pest of sugarcane in Southern Africa. Its natural habitat is sedges among riverine vegetation [1] . Eldana is the most damaging borer of sugarcane causing yield losses estimated at US$90 million in South Africa [2] . In South Africa, it was first recorded in variety POJ2725 in 1939 and later in NCo376 in 1970 [3] - [5] along the KwaZulu-Natal coast. Currently, the pest is managed in highly infested regions of South Africa by using an Integrated Pest Management (IPM) approach combining chemical control [6] , trash burning [7] , reduced harvest age, biological control, sterile insect technology [8] - [10] , push-pull technology [11] [12] and the cultivation of resistant varieties [13] .
Eldana has since spread from the coastal to hinterland sugarcane growing areas [1] . Recently, eldana damage has been recorded in the Midlands and irrigated regions of South Africa. The high altitude and cooler Midlands regions were known to experience no damage from eldana. The irrigated areas where sugarcane was harvested at 12 months also experienced little or no damage. Previous recommendations for reducing yield losses to eldana included harvesting younger crops [13] . There is increasing eldana damage in irrigated and Midlands regions as well as in younger crops, indicating the need to explore higher levels of varietal resistance.
Breeding for resistance started in the 1980s when eldana was elevated to pest status [14] [15] . Crosses were generated from parents with known high resistance and selected genotypes planted in advanced variety trials were screened in inoculation trials. Despite these efforts, few cultivars that possess high levels of resistance have been released in recent years, indicating the need to review current eldana resistance breeding strategy. To enhance the recurrent selection for eldana resistance, evaluating families in early stages is being explored [16] .
Family selection in sugarcane involves positive selection of whole populations of seedlings based on data derived from family plots [17] . Family selection in the seedling stage (Stage I) is widely practiced to different extents for cane yield and sucrose content in Australia [18] , USA [19] , India [20] and Brazil [21] , South Africa [22] . Family data can also be used to evaluate parents. Family selection has produced larger gains compared to individual genotype selection for sugarcane yield and sucrose content [23] [24] . Family selection has not been explored for pest resistance. The reported slow progress, complex and possibly quantitative genetic control of resistance, implies family section may be valuable.
In Stage II of sugarcane breeding in South Africa, genotypes selected from stage I are planted in un-replicated single row plots. Yield estimates subjected to logistic regression analysis [25] and visual field assessment are used to determine genotypes to advance. With the increased levels of eldana in the industry and the need to develop resistance, it is logical to focus intensive selection for eldana in early stages of selection (Stages I and II) where variability for damage is expected to be high and also large numbers of genotypes provide opportunity to identify genotypes that combine high values for eldana resistance in addition to other traits of economic importance.
The study objectives were to examine the potential of evaluating sugarcane families and parents by using data collected from the seedling stage (Stage I) of sugarcane breeding programmes and determine the potential of using logistic regression models for selecting for eldana resistance in non-replicated early stage genotype plots in Stage II.
2. Materials and Methods
2.1. Experimental Materials
Data were collected from Stage I (Mini-lines) and Stage II (Single lines) trials. Mini-lines trials are planted from seedlings in a tramline design while single lines are planted as single row plots of 8 metres per genotypes. Two mini-lines trials, BML12 and FML13 were used in this study. Trial BML12 was established as 1 m row plots from seedlings at Bruyns Hill research station (1012 m above sea level; 29.42S, 30.68E) the Midlands region of South Africa in 2012. Trial FML13 was established as 1 m row plots from seedlings at Pongola research station (308 m.a.s.l; 27.42S, 31.59E) in the irrigated region of South Africa in 2013. The single lines trial, BSL12 was established as 8 m single row plots at Bruyns Hill research station in 2012 and SSL12 was established as 10 m single row plots at Glenside research station (997 m.a.s.l; 29.35S, 30.77E), both in the Midlands region. Bruyns Hill research station is located on humic soils with high organic matter while Glenside research station is located on sandy soils. Pongola research station is situated on sandy clay loam soils. The long term average rainfall in the Midlands is 850 mm while in Pongola the average rainfall is 600 mm. Because of low rainfall, Pongola crop was irrigated while the Midlands is rainfed.
2.2. Data Collection
Data for BML12 and FM13 were collected in 2014. At crop maturity, 20 stalks were randomly cut from the first 20 mini-lines in a family plot. The stalks were then examined by experts in pest damage for eldana entry and exit holes and the number of damaged stalks was recorded for each family plot. In the single line trials, BSL12 and SSL12, 12 stalks were randomly cut from each genotype plot. The stalks were examined for eldana entry and exit holes and the number of damaged stalks was recorded.
2.3. Data Analysis
The data from mini-lines trials, BML12 and FML13 were subjected to analysis of variance in SAS [26] using the linear mixed model [27] ,
 (1)
(1)
where Yij is the number of eldana bored stalks of the jth family in the ith replication; Ri is the random effect of the ith replication; Fj is the effect of the jth family; FRij is the random interaction effect of the ith replication by the jth family. All variables were treated as random because the populations were a sample of the populations to be planted in these two breeding programs. The data analysis generated variance components. Variance components were generated using the COVTEST option of SAS in the model statement [27] .
The estimate of broad-sense heritability (H) for families was calculated as [28] :
 (2)
(2)
where 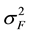 is the variance component of family effects;
is the variance component of family effects;  is the variance component of the interaction effect of replication by family; r is the number of replications. Selection gains (Gs) were estimated using the formula [29] :
is the variance component of the interaction effect of replication by family; r is the number of replications. Selection gains (Gs) were estimated using the formula [29] :
 (3)
(3)
where k is family selection intensity which is assumed to be 30% [24] and σ is the phenotypic standard deviation.
The parental effects were analyzed in SAS using the linear mixed model [28] :
 (4)
(4)
where Yijk is the number of eldana bored stalks in the jth female by the kth male parents in the ith replication; Ri is the fixed effect of the ith replication; Pj is the jth fixed effect of the jth female parent; Mk is the fixed effect of the kth male parent; PMjk is the fixed interaction effect of the jth female parent by the kth male parent; RPMijk is the random interaction effects of the ith replication by the jth female parent by the kth male parent and was the residual error.
The data for single lines trials, BSL12 and SSL12 were subjected to analysis using the logistic regression model [29] :
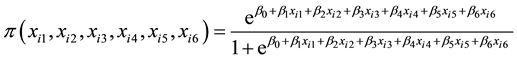 (5)
(5)
where  is the probability of selecting the ith genotype; xi1 is the ith genotype stalk
is the probability of selecting the ith genotype; xi1 is the ith genotype stalk
number; xi2 is the stalk height of the ith genotype; xi3 is the stalk number of the ith genotype; xi4 is the ERC % cane of the ith genotype; xi5 is the Fibre % cane of the ith genotype; xi6 is the eldana percent bored stalks of the ith genotype; β0 is the intercept of linear equation; β1 is the coefficient of stalk number; β2 is the coefficient of stalk height; β3 is the coefficient of stalk diameter; β4 is the coefficient of ERC % cane; β5 is coefficient of Fibre % cane; β6 coefficient of percent eldana bored stalks.
The data were analyzed using the logistic procedure of SAS. The data were divided into the training data set (10%) and prediction data set (90%). Simulations with 1% to 20% training data randomly extracted from the whole data set showed that 10% was optimum. More than 10% produced very little gains in parameter estimates while less than 10 % produced unstable parameter estimates. The prediction data had the values of the response variable coded as missing. The training data set was used to produce the parameters that were used to build the logistic regression cumulative distribution functions. The parameters generated from the training data were plugged in Equation (5). The probability of selecting a genotype was calculated by plugging in the values of stalk number, stalk height, stalk diameter, ERC % cane, Fibre % cane and percent eldana bored stalks in Equation (5), together with the variable parameters.
3. Results
Family variance for BML12 (P = 0.0144) and FML13 (P = 0.0878) were significant (Table 1). The trials produced similar estimated broad sense heritability of 0.52 (BML12) and 0.51 (FML13). The predicted gains to selection were 19.93% for BSL12 and 68.89% for FML13. The BML12 trial data produced R2 of 0.47 and FML13 produced R2 of 0.73. The BML12 trial data produced CV% of 39.6 and FML13 produced CV% of 88.9.
There were significant family effects F-values for number of eldana bored stalks for both BML12 (F value = 1.57; P = 0.0029) and FML13 (F value = 1.72; P = 0.0003) (Table 2). There were significant female effect F-values for BML12 (F value = 2.01; P = 0.0017) and FML13 (F value = 1.63; P = 0.0041). Male effects were non-significant for BML12 (F value = 1.41; P = 0.088) and FML13 (F value = 1.33; P = 0.1464). The female x male interaction effects F values were non-significant (F value = 1.39; P = 0.1532) for BML12 and significant (F value = 1.62; P = 0.0442) for FML13.
The LRM analysis produced highly significant (P < 0.0001) chi-square values for the Likelihood Ratio, Score and Wald tests (Table 3). The likelihood ratio test produced the largest chi-square value while the Wald test produced the lowest. The statistics for the BSL12 trial were larger than those for the SSL12 trial.
Analysis for the BSL12 data produced significant (P < 0.05) chi-square values for all trait values except Fibre % cane (P = 0.4914) (Table 4). The stalks, height, diameter and eldana were highly significant (0.0001) while ERC % cane was significant (P = 0.0389). The chi-square value for eldana was almost as large as that for stalk
![]()
Table 1. Variance components, broad sense heritability (H), predicted selection gains (Gs), trial mean, R2 and CV% for percent eldana bored stalks in trials BML12 and FML13.
![]()
Table 2. The F-values and their P-values for Family, Female, Male, Female x Male effects for percent eldana bored stalks in trials BML12 and FML13.
![]()
Table 3. The Likelihood Ratio, Score and Wald Chi-Square tests and their P-values for number of eldana bored stalks in trials BSL12 and SSL12.
![]()
Table 4. The logistic regression coefficients (Estimate), their standard error, Wald Chi-Square and probability of a larger value (Pr > ChiSq) for number of eldana bored stalks in trial BSL12.
height. The logistic regression coefficients in Table 4 were used the build the cumulative logistic regression cumulative distribution function in Equation (6) because it provided the best fit to data during analysis. The probability of selecting a genotype is calculated by plugging in the values of stalk number, stalk height, stalk diameter, ERC % cane, Fibre % cane and eldana bored stalks in Equation (6).
 (6)
(6)
The SSL12 data produced significant (0.05) chi-square values for all except ERC % cane (P = 0.1815) and Fibre % cane (P = 0.0825) (Table 5). Stalk numbers and stalk diameter produced highly significant (P < 0.0001) chi-square values while stalk height (P = 0.0008) and eldana (P = 0.0232) were significant. Eldana numbers produced lower chi-square and significant values in SSL12 compared to BSL12. The cumulative logistic regression distribution function is shown in Equation (7).
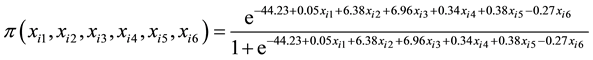 (7)
(7)
A sensitive analysis was used to determine the potential accuracy of selection using the logistic regression Equations (6) and (7), constructed from the data analysis (Figure 1). The BSL12 data produced more sensitive and more typical logistic regression trends than that of SSL12 when eldana number of bored stalks was varied from 0 to 12. For trial BSL12, using a threshold selection probability of 0.5, genotypes with more than seven eldana bored stalks will not be selection while for SSL12, a threshold selection probability of 0.8 will eliminate genotypes with more than seven eldana bored stalks.
4. Discussion
The high significant family effects indicate that eldana borer damage data collected from Stage I can be used to determine differences among sugarcane families. The significant differences among families also mean that superior families that possess low levels of eldana damage can be identified. The families with significantly low
![]()
Figure 1. Simulation of decrease in Probability of selection with increase in number of eldana bored stalks for trials BSL12 and SSL12.
![]()
Table 5. The logistic regression coefficients (Estimate), their standard error, Wald Chi-Square and probability of a larger value (Pr > ChiSq) for number of eldana bored stalks in trial SSL12.
eldana damage are expected to be made up of progenies that have low levels of eldana damage and thus possess higher levels of eldana borer resistance. Both trials produced similar and high levels of H indicating the effectiveness of selecting for superior families that possess lower levels of eldana-borer damage and thus higher levels of resistance. The similar values of H may suggest that the discriminating ability for eldana-borer damage among families was likely to be similar across these breeding populations [25] . The Midlands breeding population produced lower predicted selection gains than the irrigated population suggesting that differences for selection gains for eldana borer damage exist among breeding populations.
From this study, the Midlands population, where higher levels of eldana borer damage has been observed in commercial crops produced lower predicted selection gains than the irrigated breeding populations. Because more damage exists naturally in the Midlands, the result may suggest that natural selection exists in these populations compared to the irrigated population. The Midlands trials are harvested at 24 months crop age providing sufficient time for eldana populations to build-up and cause damage that would reduce yield. The irrigated populations are harvested at 12 months, well before natural infestation has set in and therefore are always subjected to low levels of eldana. Harvesting younger crops [14] has been recommended to control and manage eldana in commercial crops. Further, the high predicted gains could be evidence of the inherent high variability in an unselected population, suggesting that active selection against eldana damage will be effective to reduce damage even under low levels of infestation that exist in the irrigated regions. The high R2 values for the irrigated population compared to the midlands suggest that the model accounted for most of the variability in the irrigated than the Midlands. The higher CV% of the irrigated than the Midlands population suggests the larger variability in the irrigated than the Midlands population [17] .
The female parent effects for both populations were highly significant while the male parent effects were not significant indicating that maternal effects were stronger than paternal effects. This result may also be a reflection of the complexity of sugarcane flowering and flower synchronization during crossing. The result of the challenge caused by variability in flowering in sugarcane parental populations results in many of the crossing designs being melting pots or poly-crosses where one female is pollinated by several males. The result is that little is known of the contribution of the males because of lack of identity of males in crosses. The contribution to pollination of the male parents is determined by the flowering percent, percent pollen production and percentage of pollen produced that is viable as well as the length of time the produced pollen remains viable. Further, sugarcane is a complex polyploid and during meiosis, chromosomes get passed on the gametes in different fractions and can significantly deviate from the expected 1:1 ratio. In certain cases, some chromosomes get lost or transmitted in whole. This and the complexity associated with pollen viability, sensitivity and quantities further acts to reduce the contribution from male parents. The Male parents of the Midlands had smaller P-value than that of the irrigated indicated potential greater contribution of males in irrigated families. The significant Female effects indicates the potential existence of general combining ability, a results alluded to in previous studies [17] . The result suggest that the selection of parents particularly the female parent maybe more important in developing eldana resistant populations. The irrigated trial produced significant Female*Male effects, indicating the potential existence of specific combining ability. This result suggests that certain parent combinations are likely to produce better progenies when crossed. The result suggests that strategies for breeding for eldana need to include both additive and dominance effects with more emphasis on additive genetic effects. Selecting among populations for resistant genotypes for future use as parents would lead to recurrent selection for parents and lead to overall higher levels of resistance within populations. At the same time, analysis should also aim to identify combinations of parents that produce progenies with higher levels of resistance than expected to capitalise on dominance and other gene interactions.
Logistic regression models produced significant contribution of eldana damage to the selection probability. This means that selecting for eldana would be effected in non-replicated genotypes trials. Further, the result also suggests the presence of sufficient variability to be capitalized during the selection at this stage. For the Midlands population, the chi-square value of eldana damage was as large as the other yield traits such as stalk height, indicating that selection for eldana should be given equal weighting to selecting for yield and quality. Eldana bored stalks coefficient was negative indicating that as the number of eldana bored stalks increased, the probability of selecting a given genotype decreased. The result also demonstrated the importance and superiority of LRM as a selection aid [26] . Generally, the selection of a genotype would then be a balance of the important traits and their combination providing a non-biased guide to selection that combines all traits of economic importance in a population. The chi-square for eldana damage was larger than that for ERC % cane and fibre % cane indicating that within these populations, gains are expected to be larger when selecting for eldana than for quality traits. With the high levels of eldana observed in the commercial crop and the expected large yield and economic losses expected the result further highlight the importance of eldana damage in reducing yield and thus its influence of sugarcane genotype selection.
Sensitivity analysis was done to compare the selection differential between the two Midlands populations. The better fit of the humic soils population to the logistic theoretical curve compared to the sandy soils populations suggests the higher precision associated with selection for eldana among the humic soils population [26] . Less precision is expected from the sandy soils population. The variability maybe explained by the variability in the trial locations for the two breeding programmes. The sandy soils location was more variable for both slope and soil in a given field compared to the humic soils. The larger variability within a field would result in larger variability in levels of infestation of eldana. Field areas with poorer growth are likely to experience more crop stress and thus get more prone to build up of eldana than areas with good soils and better growth. Further studies may be required to quantify the field variability and accommodate them during experimental design.
5. Conclusion
Family selection would be effective in identifying families that possess higher proportions of resistant genotypes. Female parents were more significantly associated with low levels of eldana damage suggesting the additive genetic control. The significant Female x Male effects suggested existence of non-additive genetic interactions. Parent evaluation and selection would be enhanced by using family data and is expected to increase genetic gains for eldana breeding. Logistic regression showed significant contribution of eldana damage to genotype selection. Combination of family and parent evaluation and logistic regression is expected to increase efficiency of breeding for resistance to eldana borer.