1. Introduction
The offshore structures are used for various operations (drilling, breakwaters, embankments etc) in various water depths and environments.
The self-elevating unit (or jack up structure) is an offshore structure of the floating platform type equipped with three or four legs, with which the unit can lift itself up upon in order to get the hull away from the wave zone. The legs are separated and fitted with special footings designed for fixing and eventually penetration of the sea bed. The unit has to have the possibility to:
-transit, when is moving from one location to another by pushing or towing with pushers or tug boats, with the legs retracted;
-installation, in which the unit installs itself by positioning (fixing) its legs on the seabed. In this case the self lifting of the platform safely away from the wave zone is a very important operation;
-operation, when the unit is fixed on location in an elevated position with its platform above the wave zone and capable to do the designed operations;
-retrieval, when the unit retracts its legs from the seabed and is getting ready to move to other location.
Such unit, shown in Figure 1, used for Black Sea near shore all-year operations, such as quay constructions, is analyzed in the paper. In spite of diminished environmental conditions, the unit is designed so that to fulfill all requirements requested for all stages.
Design criteria of the unit have to be based on the regulations given by the Maritime Rules, such as Det Norske Veritas [1] and American Bureau of Shipping [2] requirements that have been used in this work. Generally speaking, the offshore construction project includes the certain phases [3] : concept design, structure strength calculation, basic design, detailed design, fabrication of steel structures, transportation and installation operations. In the present case, to obtain a self-elevating unit for nearshore operations, the conversion of an existing ship hull structure is performing.
The quantifying of the risk contribution from errors is one of the most important items during design phase of the maritime platform [4] . The errors can be related to structural integrity and it is necessary to consider the most critical elements that may govern the probability of error occurring for the unit.
This maritime jack up structure is loaded by static loads (the structure weight, the weights of installations, equipments and material placed on deck etc.) and dynamic loads (waves, wind, marine currents, earthquake and the operational forces provided by the equipments etc.).
The analysis of the maritime jack up type platform’s behavior during operations consists of: static, dynamic and fatigue resistance. The static calculus of the maritime platform is done in two steps: the global strength calculus and the local strength calculus, to obtain the local stresses from the global loading results (see Figure 2).
1.1. General Characteristics
The general characteristics of the jack up platform are referring to the main dimensions of the platform (treated as a ship), legs characteristics and lifting system characteristics. According to [5] , these characteristics have the values:
![]()
Figure 2. The jack up analysis flow chart.
-Main dimensions
Length over all 30.30 m
Hull length 30.00 m
Breadth 14.00 m
Depth 3.20 m
Draught 1.60 m
Lightship 300 t
Displacement 400 t
Deadweight 100 tdw
-Leg characteristics
Diameter 1.2 m
Length of lower section 20 m
Length of upper section 15 m
Allowable load on leg 150 t
-Characteristics of lifting system
Lifting speed 10 m/s
Lifting step 1.4 m
1.2. Operational Conditions
The operational conditions of the jack up platform are referring to the environmental, working, survival and navigation conditions during transit, when is moving from one location to another by pushing or towing, [5] .
-General environmental conditions
Air temperature 5˚C - 40˚C
Relative humidity (max.) 95%
Water temperature 0˚C - 35˚C
Current max. 0.35 m/s
Maximum water depth 25 m
-Working conditions
Wind speed max. 13.9 m/s (50 km/h)
Wave height in lifting position max. 2 m
Wave height during relocation max. 0.5 m
-Survival conditions
Wind speed max. 28.5 m/s (93 km/h)
Wave height in lifting position max. 5 m
-Navigation condition
Wind speed max. 14.0 m/s (50 km/h)
Wave height max. 2 m
-Legs lowered at 5 m under bottom
Rolling amplitude max. 3 deg
Pitch amplitude max. 2 deg
2. Jack up Structure Analysis
The typical offshore structure, supported by legs, normally has a deck structure that includes the certain number of decks and a helideck. In the case of the platform operating nearshore, the structure includes bottom, main deck, sides and longitudinal and transversal bulkheads. The platform structure is supported by legs through a hydraulic lifting system whose the basically components are connected to the piles as shown in Figure 3. The self elevating system is concerning of an input-output lock structure acted by the actuators provided for each leg. The local structural model consists of joints definition.
The design and analysis of a near shore jack up platform have to be done taking into consideration many factors, including the important parameters such as environmental, soil characteristics, water depth, wave and wind loads, Rules requirements, intensity level of consequences of failure.
The initial structure of the unit hull (in fact a former inland floating crane) was strengthened to be converted into the self elevating maritime platform with four tubular legs. The reinforcements have been performed in the areas of the cases for self elevating systems and the area of working equipment.
During the operating period, the platform is supported by the four tubular legs provided with lifting structure. The FEM model includes all structural members of the platform structure.
3. Environmental Loading Modeling
The loads acting on the jack up structure (Figure 4) are: platform weight (G), wind pressure (Fwind), wave action (Fwave) and current pressure (Fcurrent).
The estimation of each loading component is performed according to [1] .
The loads provided by the environmental loading are estimated using the sea state model. This model is defined by a stationary wave of short duration. The loading provided by the sea state occurs from waves, currents and wind. The sea state is selected according to the expected largest wave amplitude from the location. In Figure 3 the loading contributions within the sea state is illustrated.
Determination of wave loading is performed by using a stochastic approach or by using a deterministic approach.
According to a sea state, the stochastic approach uses a wave spectrum, characterized by a significant wave height Hs, spectral peak period Tp and a spectral peakedness parameter γ.
![]()
Figure 3. The base component of the lifting system.
![]()
Figure 4. The loads acting on the jack up structure.
The deterministic approach is characterized by the loading known at all instants of time.
In this case, the wave loading is obtained by using a single periodic extreme wave passing through the structure. This is a usual approach in analyzing the jack up units. The water particle kinematics is frequently repre- sented by a higher order wave theory.
The current loading comprises components due to tidal current, storm surge current and wind driven current.
3.1. Hydrodynamic Loading
According to the modified version of the Morison’s equation, hydrodynamic forces are composed of a nonlinear drag component and an inertia force component:
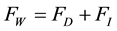 (1)
(1)
where:
FD―drag force;
FI―inertia force;
 (2)
(2)
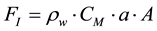 (3)
(3)
In the Equations (2) and (3) ρw is mass density of water (1025 kg/m3 for sea water), D is effective diameter (1.2 m in the case of studied unit), CD is drag coefficient (for Reynold number greater than 1 × 106, for circular section, CD is taken 1.05), v is liquid particle velocity, normal to the member, a is liquid particle acceleration, normal to the member, CM is inertia coefficient (for Reynold number > 1 × 106, for circle section, it should take CM = 1.8) and A is area of member (for the circular cylindrical leg, A = 1.1304 m2).
For the quasi-static analysis under regular sinusoidal wave action, the horizontal speed and acceleration of the liquid particle are calculated with formulas:
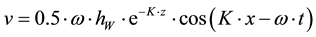 (4)
(4)
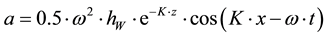 (5)
(5)
where:
z―vertical coordinate from water surface;
x―horizontal coordinate;
hW―wave height;
T―wave period.
For jack up unit location, hW = 5 m and T = 6 s.
w―wave pulsation
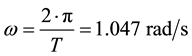 (6)
(6)
l―wave lenght, determined with the equation
 (7)
(7)
K―wave number, determined with the equation
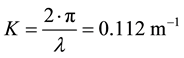 (8)
(8)
g = 9.81 m/s2―gravity acceleration.
In the working location the water depth is h = 25 m. In this case, the total drag force on the leg is determined by integrating Equation (2) along the leg axis:
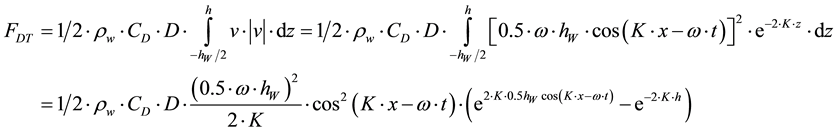 (9)
(9)
Maximum value of this force appears for unity value of cosine. Therefore
 (10)
(10)
The total inertia force on the leg is determined by integrating Equation (3) along the leg axis:
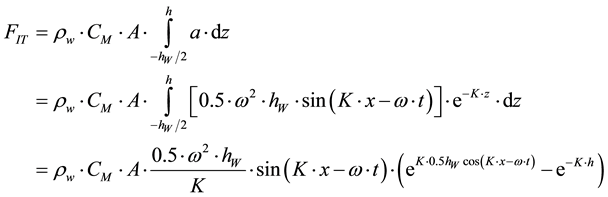 (11)
(11)
Maximum value of this force appears for unity value of sine. Therefore
 (12)
(12)
The resultant force induced by wave, FWT, has maximum value of 109.45 kN when![]() .
.
3.2. Wind Loading
The total wind force is determined by summing the wind loading acting over all structural components.
The wind loading is obtained by multiplying the pressure by the i-th projected structural component area
![]() (13)
(13)
where Aw,i is the normal projected area of the member surface and pi is the wind pressure at the element centre, given by
![]() (14)
(14)
where Cs is shape coefficient, ρa is the mass density of the air (1.225 kg/m3) and vz,i is the wind velocity in the element centre.
The resultant force induced by wind, FV, for all platform lifted to 4m above water surface under a wind of 25.6 m/s, has value of 73.4 kN.
3.3. Current Loading
The current loading comprises components due to tidal current, storm surge current and wind driven current.
The current force per unit length of legs is given by the Morison’s formula:
![]() (15)
(15)
where:
VC is current speed, determined with the equation
![]() (16)
(16)
VT is tidal current speed ;
VW is wind current speed, determined by the equation
![]()
VR1 is wind speed at 10 m above water surface for a period of one minute;
h0 is conventional depth of water for wind current (h0 = 50 m);
z is vertical distance from water surface;
h is actual depth of water.
In Black Sea area there is not tidal current (VT = 0) and for a wind speed of 20 m/s, wind current speed is VW = 0.34 m/s.
For all leg lenghts, a water depth of 25 m and wave with height of 5 m, the total current force is given by formula:
![]() (17)
(17)
3.4. The Horizontal Reactions of the Sea Bed and of the Leg Bearing
It is considered that this reactions occurs due to action of wind, wave and current (see Figure 5).
The sea bed reaction is given by the formula
![]()
and the leg bearing reactions are given by formulas
![]()
![]()
where: l = 30 m; d = 3 m; h = 25 m.
DAF is dynamic amplification factor of wave loads. Its calculated value is 1.26.
![]()
Figure 5. The external loads and reactions on leg.
4. Structural Modeling
The structural model of the platform is developed normally using a common software package developed for the steel structures. In this case the licensed CAD system was used. In Figure 6, the FEM structural model of the jack up platform is shown.
This model is suitable to perform the global strength analyses. The second step was the performing of a more detailed analysis of the single leg model to check the strength of the leg structure. The detailed leg model is related with the reactions at the spudcan and the pressures occurred in the guides, obtained from the global model.
The third step was to analyze the static and dynamic behavior of the jack up system (platform and legs).
The all structural elements of the jack up system have been modeled with shell elements.
4.1. Global Quasi-Static Analysis
The loading acting in the quasi-static analysis are:
-Gravity loads applied on all structural elements;
-Wind loads applied at hull;
-Operational forces, occurred from the working equipment (7 cases).
The seven cases are:
-Case 1―Punctual forces at each frame between frame 50 and frame 59, at 1750 mm from CL;
-Case 2―Punctual forces at each frame between frame 50 and frame 59, at 750 mm from CL;
-Case 3―Distributed forces on a surfaces of 1 m2 around the point placed at frame 42, at 1500 mm from CL, in Port side;
-Case 4―Punctual forces at frame C42, at 1500 mm from CL, in Port side;
-Case 5―Punctual forces at frame C42, at 1750 mm from CL, in Port side;
-Case 6―Punctual forces at frame C57, at 1500 mm from CL, in Port side;
-Case 7―Punctual forces at frame C57, at 1750 mm from CL, in Port side.
Since the only the global behavior of the platform hull is interested in the first step, the platform was considered as supported in the areas of the legs guides.
In Table 1, the maximum stresses are presented. For the cases where the maximum stresses exceed the permissible stresses, certain restrictions are imposes.
![]()
Table 1. Maximum stresses and permissible stresses occurred in platform structural elements.
![]()
Figure 6. The structural model of the jack up platform.
4.2. Leg Structure Strength Analysis
Various versions of the leg structure (geometry of structure, guide positions on the legs etc.) have been analysed.
In Figure 7 the final configuration of the leg geometry and loading case of the leg analysis is illustrated.
The final configuration of the FEM model is concerning: the leg length of 35 m supported by the both guides (the upper guide at 32.5 m and the lower guide at 29.5 m from the lower end of the leg). At the lower section of the leg the transversal force of 155.5 kN and longitudinal force of 2000 kN are acting. These loads occur from the reactive forces provided by the soil. In the upper end of the leg the longitudinal displacement is blocked.
The maximum equivalent stresses, of 253.37 MPa have been occurred in the cylindrical shell of the leg, in the lower guide. The same value has been obtained in the correspondence of the longerons and circular transverses, in the same transversal section. The maps of equivalent stresses occurred in leg structure are illustrated in Figure 8 (structure with shell) and Figure 9 (structure without shell). The maximum transversal displacement is of 0.516 m.
4.3. Static and Dynamic Behavior of the Jack up System
4.3.1. FEM Model
FEM analysis has been used for checking the strength and stiffness of the unit system (platform and legs).
The system has been loaded by the structure and equipment weight (2000 kN) and the environment loads (155.5 kN on each leg). To check the global behaviour of the system platform-legs, the platform has been considered as a solide structure, having the geometry and rigidity as the real structure.
4.3.2. Structural Modeling of the Jack up Unit
For a fast FEM calculus of the global structure, the simplified (equivalent) model of the legs structures has been analysed.
To simplify the leg structure (denotes with s) only longitudinal structural elements are taken into calculus.
Only elements loaded in leg general bending are considered-shell and longerons. The stresses occurred in transversal elements (web transverses) are participating at strain energy of the leg. If these elements should disappear the real strain energy of the real leg structure (jotted with r) should decrease and therefore the global rigidity of the leg should decrease.
To have the same rigidity for the real structure and the simplified structure, the shell thickness was increased. In the FEM bending calculus the maximum deflection of the real leg is 0.7 m. To have the same deflection for the simplified structure the thickness of the shell was increased with 35.6%.
The new shell thicknesses of the leg sections are:
-lower section: real thickness―16mm; new thickness for simplified model―21.7 mm.
-upper section: real thickness―18mm; new thickness for simplified model―24.3 mm.
The new leg structure has the same deflection of 0.514 mm as the real leg structure for a transversal force of 155.5 kN
The rigidity of the platform structure is bigger than the rigidity of the legs structure. Therefore, for FEM analysis of the behaviour of the jack up unit (platform on legs), the platform structure was considered as a very rigid body connected with the legs having the real rigidity.
![]()
Figure 8. Leg structure: the map of the equivalent stresses.
![]()
Figure 9. Leg structure, without shell: the map of the equivalent stresses.
4.3.3. Loading on Simplified Model
The jack up unit structure has been loaded with platform weight acting vertical (8000 kN) and environment force acting horizontal (622 kN).
The jack up unit system has been considered hinged on the level of sectional contact between legs and sea bed.
4.3.4. The Deformed Shape of the Simplified Model
In Figure 10 the deformed shape of the simplified model of the jack up unit (platform on legs) is illustrated.
The maximum displacement of the system is of 96 mm and occurs toward the horisontal forces action.
This value demonstrates that the jack up unit (platform on legs) system is stiffer than teach leg, separatelly considered, due to the compound effect of the all legs through the platform structure.
4.3.5. Reactions in the Contact Sections Legs-Sea Bed
The reactive forces values from sea bed are:
In each leg from wind direction (fore)
-vertical reaction: 1390 kN
-horisontal reaction: 156 kN
In each leg under wind direction (aft)
-vertical reaction: 2611 kN
-horisontal reaction: 156 kN.
4.3.6. Natural Vibrations
Due to the equipment acting on platform and due to the environment forces, it is necessary to know the natural frequencies of the jack up system. Therefore, a dynamic calculus to determine the natural frequencies and modal shapes have been performed. In the Table 2, the natural frequencies and the corresponding modal shapes are presented.
In Figures 11-13 the modal shapes according to the natural frequencies of the jack up rig are illustrated.
![]()
![]() (a) (b)
(a) (b)
Figure 10. The deformed shape of the jack up unit ((a) 3D view; (b) 2D view in the plane of the external forces).
![]()
Table 2. The first three global natural modal vibrations.
![]()
Figure 11. First global torsion mode (f = 0.207 Hz).
![]()
Figure 12. First global bending mode in plane YZ (f = 3.019 Hz).
![]()
Figure 13. First global bending mode in plane XZ (f = 5.001 Hz).
5. Conclusions
The objective of this paper is to present a method of global and local strength assessments analysis by which it is be possible to perform a retrofit of an old floating crane structure into a maritime self-elevating platform.
Taking into account the life cycle of the initial structure (25 years) the criteria used for the platform design were penalized with heavy factors [6] .
Various parametric analyses have been performed for the platform structure, leg structure and their sensi- tiveness to the various responses have been estimated. The parameters considered are variations in water depth airgaps and structural modifications (dimensions and geometry).
After a set of calculations, including the changing of the geometry, the acceptable stresses have been obtained in the leg structures and platform structures.
Results from the parametric analyses showed that the “tailor-made” jack up unit studied has to be strengthened in order to satisfy the Rules requirements.
The hull structure design and calculus criteria fulfill the ABS Rules requirements for the operational conditions.
The operation loads determined according to the DNV Rules are adequate to the work conditions (operational profile).
The final geometry of the platform structural elements has been obtained after an iterative calculus procedure.
The stress states in all loading cases show maximum values not exceeding the permissible stresses in the following certain conditions:
-The moving working equipment (excavator) mass will not exceed 100 tons;
-In the deck working area a wood pad of 50 mm thickness will be provided, so that the loads transmitted by the caterpillar chain to be uniform distributed on deck structure and to avoid the equipment lifting. These remarks are followed by the results obtained in cases 6 and 7;
-Certain details on the excavator working procedure should be provided;
-It is forbidden to operate in the area between frames 37 and 48 (according to the results obtained in cases 3, 4 and 5).
Acknowledgements
The work has been performed in the scope of the Romanian Project 650/2015/University Dunarea de Jos of Galati, Romania.
NOTES
*Corresponding author.