Structural Deformation Monitoring and Analysis of Highway Bridge Using Accurate Geodetic Techniques ()
1. Introduction
Structural health monitoring is the term that describes the range of systems implemented on various civil infrastructures, which inform operators whether the structural deformation is the same as those the structure was designed to tolerate or not [1] . The demand for structural health monitoring systems for bridges has grown over the last few decades [2] . In order to know the safeties of bridges, monitoring their real-time displacement and recording their fatigue history are very important.
The measuring techniques and instrumentation for geometrical monitoring of structural deformations have traditionally been categorized into two groups according to the two main groups of professionals who use the techniques [3] :
1) Geodetic surveying, which includes Global Position System (GPS), close range Photogrammetry, terrestrial surveying (leveling, theodolite, total station and very long base line interferometer) and satellite laser ranging.
2) Geotechnical structural measurements of local deformations using tilt meters, strain meters, extensometers, joint meters, laser distance gauge method, etc.
Each type of the measurements has its own advantages and drawbacks [1] . The acceleration integration method integrates the acceleration, which is measured by acceleration gauge, to obtain the displacement. But its error is relatively large. The laser distance gauge method is often influenced by the weather. Furthermore, the geotechnical structural measurements often need to stop the traffic, which brings a lot of costs. So these methods are suitable for some structures whose survey distance is relatively short and the displacement is relatively small. But to structures such bridges, these methods are difficult to use.
Geodetic surveys, through a network of points interconnected by angles and distances measurements, usually supply a sufficient redundancy of observations, for the statistical evaluation of their quality and for detection of errors [4] [5] . They give global information on the behavior of the deformable object. Recent advances in technology have made it possible to use accurate surveying equipments to measure and monitor the deformation of structural members. The emergence of reflectorless accurate total station allows working without special reflectors (prisms). It is now possible to measure without long and tedious search of prisms to lift the reflector under the roof of buildings. The principle of work of reflectorless total station is the same as that of a simple total station [6] .
The surveillance of an object involved in a deformation process requires the object as well as the process to be modeled. Conventionally, geodetic modeling the object (and its surrounding) means dissecting the continuum by discrete points in such a way that the points characterize the object, and that the movements of the points represent the movements and distortions of the object. This means that (only) the geometry of the object is modeled [6] . Furthermore, modeling the deformation process means conventionally to observe the characteristic points in certain time intervals in order to monitor properly the temporal course of the movements. This means that (only) the temporal aspect of the process is modeled. Nowadays, for the analysis and the interpretation of structural deformations, different deformation models have been developed [7] . In deformation monitoring studies, these models include static, kinematic and dynamic models. Static model that is not dependent on time provides the determination of deformations on the characteristic points of the area or the structure, which is monitored. In this paper, statistical tests of geodetic observations using F-Fisher criterion with a confidence level of 98% were applied. Kinematic models allow estimating the velocity and even the acceleration (by building double differences) of monitoring point movements. The intention of kinematic models is to find a suitable description of point movements by time functions without regarding the potential relationship to causative forces.
In Egypt, there are many highway bridges with different lengths and widths which have a great effect on Egyptian life and economy. These bridges were constructed from different materials such as reinforced concrete, steel and wood. In this paper, studying the deformation behavior of one of the most important bridge in Delta Egypt is presented.
2. Observation Sites and the Proposed Geodetic Monitoring Technique
Kafr El-Sheikh highway bridge has been chosen for the purpose of the deformation monitoring study. This bridge was suited in Kafr El-Sheikh city. This city is the capital of Kafr El-Sheikh governorate in Egypt and located in the middle of the Nile Delta, where it overlooks the Mediterranean Sea Shore in the north and the River Nile (Rashid Branch) in the west. The international coastal highway (which joins all the Mediterranean Sea countries) passes in the north of it. Kafr El-Sheikh city lies 140 km north of the capital Cairo, 90 km east of Alexandria. The area of Kafr El-Sheikh city is 4.64 km2. The studied highway bridge connects Kafr El-Sheikh city to the international coastal highway and surrounding cities and villages. Kafr El-Sheikh highway bridge (Figure 1), has a total length 216 m and a width 17 m with average height 7.55 m above ground level. The highway bridge has four lanes in two ways directions. It was made of reinforcement concrete except one span was made of steel (this steel span is constructed over Meet Yazid Channel, Figure 1). The bridge was supported on ten pillars and two abutments. The bridge is subjected to two types of loads; the first type is static load (dead load), which includes the own weight of the bridge (superstructure and covering materials). The second type is moving loads (live loads); these moving loads are the transportation on the bridge.
The suggested monitoring system of bridge consists of small horizontal geodetic network around the bridge and selected monitoring points distributed on the bridge to cover its full length in its two sides. The main objective of the designed network is to provide a number of stations whose relative and absolute positions, are accurately established. More detailed location of monitoring points on the bridge are then carried out from these stations. This network (Figure 2) consists of two braced quadrilaterals figures (each figure contains four corner stations and observed diagonals). For base line observations, two GPS dual frequency receivers were used. The observations of horizontal network were horizontal and vertical angles and 10 distances, such a combined system of measuring angles and distances represents the strongest network for creating horizontal control. The angles were measured on five arcs and the distances were measured 10 times. Then the coordinates of network stations were calculated using least squares adjustment technique. The observations of geodetic network were done only one time at the first epoch of monitoring observations (December 2011). All stations of geodetic networks were fixed in stable positions. Before starting the process of first observations epoch for the bridge monitoring, site reconnaissance and topographic surveying of the bridge area were done.
Each side of the studied bridge contained 23 monitoring points (targets); the spatial distribution of these points should provide complete coverage of the bridge. The monitoring points were located where the maximum deformation values have been predicted (at middle distance of each span), plus a few points which was depending on previous experience could signal any potential unpredictable behavior (targets above each support). These
![]() Positions 1, 2, 3 and 4―Traffic flow count and noise measurementsPositions 2 and 4 are fixed on the bridge
Positions 1, 2, 3 and 4―Traffic flow count and noise measurementsPositions 2 and 4 are fixed on the bridge
Figure 1. Topographic survey of the studied highway bridge (Kafr El-Sheikh Bridge) and positions of traffic flow count and noise measurements.
![]() CP1, CP2, CP3, …, CP6―Control Points (stations of geodetic network)RS1, RS2, RS3, RS4―Reference Stations around the highway bridge
CP1, CP2, CP3, …, CP6―Control Points (stations of geodetic network)RS1, RS2, RS3, RS4―Reference Stations around the highway bridge
Figure 2. The geodetic monitoring network around the studied highway bridge (Kafr El-Sheikh Bridge―Egypt).
points (targets) were located using sheet prisms with diameter (1 cm) fixed on the superstructure of the bridge, which were securely fastened and arranged to be visible from the positions of the used two total stations. Common sense helped to reduce errors in the field. There were four reference stations outside the bridge (Figure 2) and not far from it (RS1, RS2, RS3 and RS4). These stations fixed in stable soil. Using even more reference stations was always a possibility; however, there has never been a discrepancy between all four reference stations during testing to date. The monitoring points on the bridge were observed from the four occupied stations (CP3, CP4, CP5 and CP6; Figure 2). Four epochs of observations for studying the structural deformation of studied bridge were performed at December 2011, May 2012 December 2012 and June 2013.
The used equipments consisted of: Two GPS dual frequency receivers (Sokkia), two total stations GeoMax with accessories which have the accuracy of measuring angles equals to 1'' but the accuracy of measuring distance was 2 mm ± 2 ppm for reflector measuring and 3 mm ± 3 ppm for reflector-less measuring; four tripods, 2 plumb bobs; sheet prisms; two prisms of diameter 5 cm; two survey umbrellas; and two foot plates.
Calibrations of the used instruments were preformed to confirm the specified accuracy for measuring distances and angles. The higher accuracy required for structural health monitoring demanded extra measures to assure desirable results. Most of these additional measures were fairly obvious; the goal was to reduce or eliminate the possibility of undesired instrument and target movement.
3. Determining the Coordinates of Monitoring Points on the Bridge
The two total stations technique was used to determine the spatial coordinates of monitoring points on the bridge and reference stations. This model employees the intersection process in three dimensions coordinates. If there were two known coordinates stations (XA, YA, ZA) and (XC, YC, ZC) from geodetic network and there were three unknown parameters (XB, YB, ZB) and six observations from the two total stations (two slope distances S1, S2, two horizontal angles α1, α2; and two vertical angles γ1, γ2). The parametric least squares adjustment technique will be applied to get the adjusted values of unknowns as following:
The two measured slope distances (S1, S2) from total station to the monitoring point on the bridge can be written as:
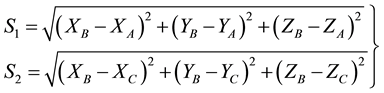 (1)
(1)
By using the coordinates formulae, the horizontal angles (α1 and α2) can be written in the following form:
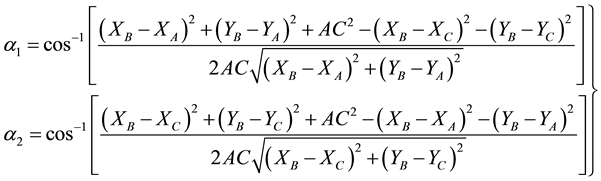 (2)
(2)
The two vertical angles (γ1 and γ2) can be calculated in the coordinates form as following:
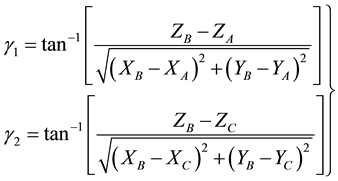 (3)
(3)
The Equations (1), (2) and (3) are the six observational equations, these equations are nonlinear function of both parameters and observations; the cofactor matrix (Q = W−1) of the observations were formed for each point. This matrix has the dimensions (6, 6) and has the form:
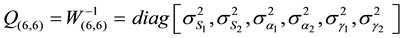 (4)
(4)
In which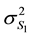 ,
, 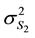 ,
, 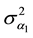 ,
,  ,
, 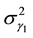 ,
, 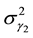 are the standard deviation of observations and can be determined by instrument calibration. In this model, all observations were assumed to be independent and uncorrelated.
are the standard deviation of observations and can be determined by instrument calibration. In this model, all observations were assumed to be independent and uncorrelated.
4. Applying Seven-Parameter Transformation for Structural Deformation Monitoring
The used data for analysis the structural deformation of the studied bridge are the coordinates of monitoring points (targets). The coordinates of these points were calculated depending on the occupied stations coordinates. So any deviations in coordinates of control points between original and repeated observations epochs will affect the coordinates of monitoring points and consequently affect the values of structural deformation.
To overcome this great problem, four reference stations were selected not far the studied bridge and fixed in stable soil. The resulted deviations (differences) of these reference stations coordinates between epochs were very small and didn’t mean that these points were moved or deformed. In geodesy, there are no identical coordinates of points between two epochs of observations [2] . The deviation in coordinates resulted from systematic errors in observations (temperature, air pressure, instrumental errors, and observations in different times of day… etc.). Then the following steps were done:
1) Carrying out transformation of reference stations coordinates from any other epoch of observations (second, third, fourth…) to the coordinates of the first epoch of observations by using seven parameters transformation to find these parameters.
2) Depending on the resulting parameters of transformation, the coordinates of all monitoring points of the other epochs of observations (second, third and fourth) were transformed to the system of coordinates of the first epoch of monitoring process. By this way, any small deviations in the monitoring points coordinates were removed.
Seven-parameters transformation is used for relating the original and repeated coordinates of the original points using the following form:
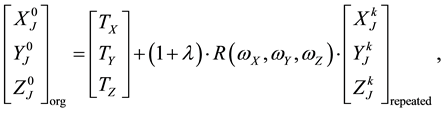 (5)
(5)
where:  = Original coordinates of reference point J at the first epoch of observations;
= Original coordinates of reference point J at the first epoch of observations; 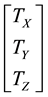 = Vector of translation components;
= Vector of translation components; 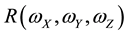 = Rotation matrix;
= Rotation matrix; ![]() = coordinates of the same points in
= coordinates of the same points in
the other cycle of observations (repeated coordinates); ![]() = The scale factor; ωX, ωY, ωZ = the rotation components.
= The scale factor; ωX, ωY, ωZ = the rotation components.
Since the values of rotation components (ωX, ωY, ωZ) will be too small, the rotation matrix can be simplified and the Equation (5) can be written as:
![]() (6)
(6)
If the identical points in the two system coordinates (in this case, the reference stations near the bridge) are more than three, the least square theory must be applied to find the seven transformation parameters [8] . The mathematical model for this case (parametric least square) will have the form:
![]() (7)
(7)
where:
m―The number of equations (in this case m = 3n);
n―The number of identical points (for the studied bridge n = the number of reference stations = 4).
The elements of matrix A can be determined by differentiate the Equation (6) with respect to the parameters of transformation. The steps of solving using parametric least squares method were applied to find the seven transformation parameters. If the coordinates of reference stations are identical, the seven parameters will equal zero.
5. Statistical Tests of Geodetic Observations for Bridge Deformation Values
Statistical tests are widely used to determine if a given quantity (coordinates of points in first epoch observations) is compatible with, or significantly different from, some other quantity. Statistical tests on the residuals would determine which of the above statements is supported by the data. For network adjustments, statistical testing is widely used for data quality assessment. So the statistical tests can be used to detect whether there are any significant coordinates differences between each two epochs of observations.
This model of the observations analysis does not consider the time intervals between the observations nor the factors responsible for the deformation―explicitly. The first step in statistical test is forming the vector of the coordinate differences of monitoring points at two different epochs at initial time (first epoch of observation) and tk, and its cofactor matrix. Point displacements ΔJ are calculated by differencing the adjusted coordinates of this point J for the most recent survey campaign (k), from the coordinates obtained at initial time as follows:
![]() (8)
(8)
where:
![]() = the adjusted coordinates of monitoring point J at time tk;
= the adjusted coordinates of monitoring point J at time tk;
![]() = the adjusted coordinates of monitoring point J at first time of observations (initial epoch);
= the adjusted coordinates of monitoring point J at first time of observations (initial epoch);
![]() (m = number of observations epochs);
(m = number of observations epochs);
![]() (n = number of monitoring points on the bridge).
(n = number of monitoring points on the bridge).
The vector of root-mean-square error (RME) of the coordinate differences can be calculated by using the matrix form as following:
![]() (9)
(9)
where:
![]() = The accuracy of coordinates of point J at time tk;
= The accuracy of coordinates of point J at time tk;
![]() = The accuracy of coordinates of point J at first epoch of observations.
= The accuracy of coordinates of point J at first epoch of observations.
Statistical test analysis for structural deformation observations can be done using several models and criteria for approval in the study of distribution laws of geodetic measurements. In this paper, F-Fisher criterion with a confidence level of 98% was applied to test the movement of each monitoring point on the bridge statistically. For achieving that goal it is important to calculate the factor ТG in dependence on the resulted values of coordinate displacements vector and vector of its accuracy (RME vector) as following:
![]() (10)
(10)
where:
![]() = Rank of matrix;
= Rank of matrix;
![]() = generalized variance of the process.
= generalized variance of the process.
The value of generalized variance of the process can be determined by applying the following formula:
![]() (11)
(11)
where:
![]() ,
, ![]() = variance factors at time k and at first epoch (initial time);
= variance factors at time k and at first epoch (initial time);
![]() ,
,![]() ―the degree of freedom at time k and at first epoch.
―the degree of freedom at time k and at first epoch.
If the test value TG is greater than the critical value, i.e.![]() , (where
, (where![]() ―confidence level), then there are statistically significant deformation in the common points.
―confidence level), then there are statistically significant deformation in the common points.
Statistical test was done for each monitoring point on the studied bridge individually for all observations epochs.
6. Traffic Flow Count on the Studied Bridge
Data collected from long-term monitoring have shown that the quasi-static and dynamic response of a bridge may change, depending on the environmental and operating conditions [9] . Contributors are found to be ambient temperature, wind speed and direction, humidity, solar radiation and vehicular loading. All of these loadings lead not only to a direct response from the structure, but can also affect physical parameters and mechanisms in a bridge. Daily traffic is the main live load which has significant impact on the strength and serviceability of bridges. Bridge/vehicle interactions have been studied since the middle of 20th century [10] . The impact of a vehicle on a bridge was initially assumed to be a moving load without considering the inertia effect [11] . Later, a vehicle was simplified as a moving mass which can consider the inertia effect on bridges. In recent years, the commonly-used analytical model for vehicle is a dynamic system consisting of mass, spring and damping parts, which have significant effects on dynamic analysis of vehicles and interactions with other systems. Thus, the interaction analysis of bridge and vehicles is to investigate the coupling nature of multiple dynamic systems. By numerically solving the coupled equations in the time domain, the dynamic response (displacement, acceleration and stress) of the bridge and vehicles can be obtained, respectively [12] . In this paper, traffic flow count and noise measurements were preformed in the two directions of the studied bridge (Figure 1).
The evolution of traffic flow is complicated in terms of vehicle number, vehicle type combination and drivers’ behavior such as lane-changing, acceleration or deceleration [13] . With relation to the volume of traffic using the road, the passenger car is adopted as the standard unit and other vehicles are assessed in terms of passenger car units (pcu). Average daily flow from traffic count in the first two epochs of observations are presented in Table 1 for the selected four count positions (Figure 1). Simple regression analysis was done to indicate the relationship between time and traffic volume.
Noise measurements were carried out in the selected positions near the bridge using 407730 Digital Sound Level Meter. The device was used after calibration by using a calibration unit of model. The Digital Sound Level Meter measures and displays sound pressure levels in dB from 40 to 130 dB. The duration of measuring was 5 hours (from 9:00 am to 2.00 pm) and the readings were recorded every 10 minutes. All readings were recorded when the digital sound level meter is placed at distance of 0.5 m from the body of the observer and at height of 1.20 m from the floor level. From the results of traffic flow count and noise measurements, it is deduced that:
・ About 40% of all traffic flow cross on the studied bridge;
・ All the recorded noise levels in all positions around the studied bridge are much more the permissible limits according to the Egyptian law of environmental and world organizations limits;
・ The noise level decreases when the traffic volume increases;
・ Simple regression analysis indicated that, traffic volume and running speed increases the noise level. Whereas traffic volume only decreases the noise level in undivided roads.
![]()
Table 1. The values of average traffic flow count around the studied highway bridge.
7. Results and Analysis
The steps for bridge monitoring were carried out according to the following procedure:
1) In the first epoch of observations (December 2011), the coordinates of the first two control points (CP1 and CP2, Figure 2) were determined from GPS observations. Then the horizontal geodetic network were fixed on stable positions and observed (16 horizontal, vertical angles and 7 distances). The most probable values were then calculated for all angles and distances.
2) The adjusted coordinates of all stations of network were then determined depending on the coordinates of the two control point (CP1 and CP2, Figure 2) using conditional least squares adjustment technique.
3) The reference stations and monitoring points (targets) for each bridge side were observed (13 points on each side) from two total stations fixed at control points in the same time. Then the coordinates of all points were calculated applying the mathematical model presented for each epoch of observations.
4) Before determining the values of deformation, the coordinates of reference stations must be checked to have the same coordinates. In our case there were small deviations between these coordinate as mentioned in Table 2. So Seven parameters transformation were applied to remove these deviations for all observation epochs.
5) Depending on the resulted new coordinates of monitoring points after applying transformation parameters, the analysis (statistical test) of observations were done.
By applying the least square adjustment technique, The adjusted coordinates and its associated accuracy of each point in the monitoring network on the bridge were calculated for all epochs. The standard deviations of monitoring points coordinates for the first observations epoch on the bridge (December 2011) were varied from 1.26 mm to 4.38 mm in the horizontal components, and from 1.3 mm to 7.63 mm in vertical component. While in the second epoch (May 2012), the corresponding values are varied from 1.19 mm to 4.93 mm in horizontal components and from 1.52 mm to 7.59 mm in vertical component. For third observation epoch (December 2012), the standard deviations points coordinates were varied from 0.88 mm to 5.24 mm in the horizontal components, and from 0.79 mm to 6.77 mm in vertical component. Practically, the overall data analysis has shown that the qualities of the observation for all campaigns are good.
The deviation of reference stations coordinates between four observations epochs and the calculated seven parameters transformation were done. Sample of results is presented in Table 2. From the results, it is deduced
![]()
Table 2. The deviation of reference stations coordinates between three observations epochs and the calculated seven parameters transformation.
that the deviations in reference station coordinates were very small for all observations epochs and varied from 42.23 mm to 1.19 mm.
From statistical test, the difference in monitoring points coordinates exceeds the expected surveying error at several points on the bridge and this is likely due to actual movement of these points. It is deduced that there are some monitoring points were moved (deformed) between the period from December 2011 to May 2012. The maximum value of deformation in this period was 8.3 cm in horizontal component and 4.7 cm in vertical direction. In the other hand, from the period December 2011 to June 2013, more points were moved.
8. Conclusions
Based on the results obtained, the following conclusions can be summarized:
1) The proposed geodetic monitoring techniques can provide valuable data on the deformation of the structural members and movement of structures such as highway bridges. The accuracy of the monitoring target coordinates will be improved if the two total stations are applied instead of using one total station only.
2) Application of seven parameters transformation technique is an effective method for determining the values of deformation of structure because it can remove the systematic errors of observations between the two successive epochs;
3) Achieving the required accuracy for geodetic monitoring technique of highway bridge is based on the following factors:
a) The used instruments specifications (Instrument resolution, data collection options and the proper operating instructions).
b) The field observing and modeling procedures. Measurements and adjustment techniques of the network have direct influence on the detection of monitoring point’s displacements;
4) All the recorded noise levels in all places around the studied highway bridge are much more the permissible limits according to the Egyptian law of environmental and world organizations limits;
5) Statistical test using F-Fisher criterion with a confidence level of 98% can be used to identify the values of deformation for any structure such as bridge between any two epochs of observations.
Acknowledgements
The author wants to thank students of Civil Engineering Department, Higher Institute of Engineering and Technology-Kafr El-Sheikh, Egypt for helping in the field observations collection.