1. Introduction
The reason for writing this article was a solution of the ancient problem. This problem in a simplified version is as follows: Slandy a noble woman well-known in the Eastern world lived in ancient times. She had seven daughters. Slandy always wore aтamazing beauty antique necklace of precious pearls, which according to tradition passed from mother-in-law to daughter-in-law. In old age, she told her daughters-in-law: “By inheritance it is time to pass the necklace to someone of you and if I will choose someone of you, the others will be offended. If I choose two of you and divide this necklace exactly into two parts, one pearl will be surplus. This is not a right way plus other fives will feel aggrieved what I don’t want in my old ages. And also, when this necklace is divided into 3, 4 or 5, and 6, in each case one pearl is superfluous. And if I divide it by 7, the pearls split evenly, but this is also impossible, as this necklace according to the covenant of ancestors must be passed to only one daughter-in-law. Therefore I will pass the necklace to whom who will determine how many pearls are in this necklace. Others should not be offended.”
“It is known that the daughter-in-law, who decided this problem called Alkhan-Tumar, which means Necklace-Mascot.
Legend also says that this necklace still exists.”
Naturally today it is not difficult to solve the problem. Let’s first recall Wilson’s theorem which is formulated as: a natural number n > 1 is a prime number if and only if 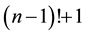 is divided by n evenly [1] .
is divided by n evenly [1] .
This formulation implies that 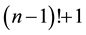 is divided by all natural numbers less than n (except 1) with a remainder of 1. Using given theorem, let’s find a solution: 721. However, it is not a full solution and it is one of a set of solutions.
is divided by all natural numbers less than n (except 1) with a remainder of 1. Using given theorem, let’s find a solution: 721. However, it is not a full solution and it is one of a set of solutions.
Using criterions for divisibility and properties of natural numbers factorial expansion, we can find a first solution as 301. Obviously, that the solutions of this problem set up an arithmetic progression, the first term of which is equal to 301 and the progression difference is 420. i.e. the sequence of solutions of this problem looks like: 301, 721, 1141, etc.
This example is interesting because, if in this problem we replace last number 7 by number 9, or by any composite number, then this problem has no solution, since a condition of a remainder of 1 will not be fulfilled. In short, this problem has a solution when and only when a final number is a prime number, such as 11, 13, 
As you can see, this problem is devoted to the problems of prime numbers. We believe that such problems with some similar formulations can be found in folklores of many nations. This is not surprising, the problems of prime numbers appeared before the Common Era, have been affecting interests of the scientific community for more than 2300 years. Since Eratosthenes, scientists have been gradually progressing, and in recent decades computers appeared to help them. But the main problems of prime numbers are still unsolved.
The solution of the above mentioned problem shows a way for solving the following problem of prime numbers.
2. Prime Numbers Generation
Let we solve the following problem.
Suppose we are given an ordered sequence of prime numbers. It is necessary to find a next in order prime number. To solve the problem the following theorem is suggested.
Theorem. If the numbers 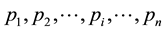 are terms of the original sequence of prime numbers, where is an order of a prime number, i.e.
are terms of the original sequence of prime numbers, where is an order of a prime number, i.e.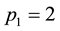 ,
, 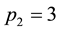 ,
, 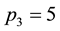 ,
,  , etc., then there is a whole number k for which
, etc., then there is a whole number k for which 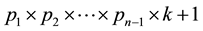 is divided evenly by
is divided evenly by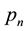 , and by
, and by 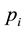 with a remainder of 1 for all
with a remainder of 1 for all 
It is easy to prove this theorem. For this purpose, it is only necessary to combine Wilson’s theorem with a fundamental theorem of arithmetic (“every natural number greater than 1 can be represented as a product of prime numbers, and this product is unique”). The combination of these theorems makes required proof elementary and obvious. For this purpose, in a first approximation, it suffices to take as a product of all composite numbers less than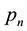 , i.e. a product of those composite numbers that appear in Wilson’s theorem. Therefore, we skip a proof of the theorem intentionally.
, i.e. a product of those composite numbers that appear in Wilson’s theorem. Therefore, we skip a proof of the theorem intentionally.
Now, using this theorem, we will show an algorithm for solving posed problem.
3. Algorithm for Generating Prime Numbers
Suppose we have a sequence of known prime numbers , where i is an order number of prime numbers, i.e.
, where i is an order number of prime numbers, i.e.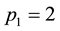 ,
, 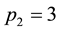 ,
, ![]() ,
, ![]() , etc. and
, etc. and ![]() desired prime number.
desired prime number.
Let indicate ![]() as a product of
as a product of![]() . Therefore, according to the conditions of the suggested theorem, for some whole number
. Therefore, according to the conditions of the suggested theorem, for some whole number ![]() the following equality should be satisfied:
the following equality should be satisfied:
![]() , (1)
, (1)
Lemma. If equality (1) is true, then it is true for a infinite set of whole values of k. Plus a sequence of values of k forms an arithmetic progression, the first member of which is in interval from 1 to![]() , a common difference of this progression is equal to
, a common difference of this progression is equal to![]() , and one of the terms of the progression is a product of all composite numbers less
, and one of the terms of the progression is a product of all composite numbers less![]() , i.e. a product of those composite numbers that appear in Wilson Theorem.
, i.e. a product of those composite numbers that appear in Wilson Theorem.
4. Proof
For optimality of the proposed theorem implementation in practice, we need to determine a minimum, i.e. the initial value, of k or at least to identify an interval it belongs to.
For this we consider the ratio of![]() .
.
First we will show, that, if the ratio at any k from 1 to ![]() is not a whole number, then it will not be a whole number for any
is not a whole number, then it will not be a whole number for any![]() . Let prove this.
. Let prove this.
Suppose an expression ![]() at
at ![]() is not a whole number. Let try to determine, what
is not a whole number. Let try to determine, what
this ratio will be for the next following values of k For this purpose we select a value of![]() . Then the ratio in question takes a form as:
. Then the ratio in question takes a form as:
![]()
It is obvious, that this expression will not be a whole number, since an addend, as mentioned above, is not a whole number. After that, repeating this procedure similarly for any![]() , we assure that this ratio will never be a whole number.
, we assure that this ratio will never be a whole number.
This means that, if the ratio in question of Equation (1) is a whole number, then the initial value of k must be in interval from 1 to![]() , i.e. if
, i.e. if
![]() .
.
We will also show here that when the equality (1) is satisfied, the parameter k takes a set of values that equal to![]() . In fact, using this expression, we transform the original ratio in question into:
. In fact, using this expression, we transform the original ratio in question into:
![]()
It is obvious, that the first term is a whole number and the second term, as was shown above, is also a whole number, therefore the ratio in question in the lump is also a whole number.
From the above said it follows that under the equality (1), the parameter k takes is a set of values which, as stated above, form an arithmetic progression. The first term of the progression should be in interval from 1 to![]() , i.е.
, i.е.![]() . The common difference of this progression is equal
. The common difference of this progression is equal![]() . One of the terms of the arithmetic progression is a product of all composite numbers less than
. One of the terms of the arithmetic progression is a product of all composite numbers less than![]() , i.e. it is equal to the product of those composite numbers that appear in Wilson’s theorem.
, i.e. it is equal to the product of those composite numbers that appear in Wilson’s theorem.
5. The Proof of the Lemma Is Completed
From this moment and further, it is sufficient to know an initial value of parameter k, which is in interval of![]() . For convenience, we introduce parameter
. For convenience, we introduce parameter![]() , such that
, such that![]() .
.
Note that expression of Equation (1) includes two conditions:
a) A number ![]() should be separately divided by all
should be separately divided by all ![]() with a remainder 1, i.e. for all
with a remainder 1, i.e. for all![]() :
:
![]() (1а)
(1а)
b) A number ![]() should be divided by
should be divided by ![]() evenly, i.e.
evenly, i.e.
![]() (1b)
(1b)
Thus, let we have an initial ordered sequence of prime numbers ![]() To find the next in order prime number
To find the next in order prime number ![]() we will build the following algorithm. For this, first for
we will build the following algorithm. For this, first for ![]() we take the next odd number to
we take the next odd number to![]() . After that, taking k from 1 to
. After that, taking k from 1 to![]() , we execute arithmetic operation given in Equation (1). If in this case and at some value of k the conditions of Equations (1a) and (1b) will be observed, i.e. a result of division according the Equation (1) will be a whole number and then considered number
, we execute arithmetic operation given in Equation (1). If in this case and at some value of k the conditions of Equations (1a) and (1b) will be observed, i.e. a result of division according the Equation (1) will be a whole number and then considered number ![]() is the next prime number. After that, in the same way we start to search next prime number
is the next prime number. After that, in the same way we start to search next prime number![]() .
.
And, if the conditions of Equations (1a) and (1b) are not met, then we deal with a composite number, i.e. in this case, considered number of ![]() is not a prime number. It should be noted here that if the number
is not a prime number. It should be noted here that if the number ![]() will be a composite number, then during the calculation of
will be a composite number, then during the calculation of![]() , a sequence of digits of the fractional part of
, a sequence of digits of the fractional part of
this division result is periodically repeated while sorting parameter k. It can be easily seen after a few steps of cycle by k parameter, and it becomes clear that considered number ![]() is not a prime number. Then we can immediately stop the cycle. This greatly increases the efficiency and speed of the proposed algorithm.
is not a prime number. Then we can immediately stop the cycle. This greatly increases the efficiency and speed of the proposed algorithm.
Then we proceed to the next odd number. The procedure is repeated again for different values of k.
If even in this case, the selected number is again a composite number, then proceed again to the next odd number. The operation is repeated until the conditions of Equations (1a) and (1b) will not be fulfilled. For clarity, we will show this based on a simple example.
Suppose we have an original sequence of prime numbers![]() ,
,![]() . It is required to find the next fifth prime number
. It is required to find the next fifth prime number ![]() In this case,
In this case,![]() . For this, first for
. For this, first for ![]() we take 9 as an odd number next to 7. Then we calculate the values of
we take 9 as an odd number next to 7. Then we calculate the values of ![]() for different values of k from 1 to
for different values of k from 1 to ![]()
![]()
![]() , etc. As can be seen, the values of
, etc. As can be seen, the values of ![]() constitutes an arithmetic progression with a difference of
constitutes an arithmetic progression with a difference of![]() . Note that among these values 841 and 1261 are composite numbers, and the rest of them are prime numbers. But we are looking for a prime number following 7.
. Note that among these values 841 and 1261 are composite numbers, and the rest of them are prime numbers. But we are looking for a prime number following 7.
Conducting the series of calculations, we see that a result of division of ![]() at any value of
at any value of ![]() will
will
not be a whole number. This means that 9 is a composite number. After that for ![]() we take the next odd number 11. Repeating the operation we obtain that at k = 10 value of
we take the next odd number 11. Repeating the operation we obtain that at k = 10 value of ![]() is divided by 11 evenly. Actually, 2101:11 = 191. This means that a prime number next to 7 is 11, i.e.
is divided by 11 evenly. Actually, 2101:11 = 191. This means that a prime number next to 7 is 11, i.e.![]() .
.
For completeness of the visualization, we consider one more sequence of prime numbers, with its last term as 23. In this case, first for ![]() we take 25 as an odd number, next to number 23. And we see that it is a composite number. Then we select a number 27. At this time, the condition of Equation (1) will not be fulfilled, that is, we see that 27 is a composite number. When we select number 29, then at k = 17 condition of Equation (1) is satis-
we take 25 as an odd number, next to number 23. And we see that it is a composite number. Then we select a number 27. At this time, the condition of Equation (1) will not be fulfilled, that is, we see that 27 is a composite number. When we select number 29, then at k = 17 condition of Equation (1) is satis-
fied, i.e. a value of ![]() is a whole number. This
is a whole number. This
means that a prime number after 23 will be 29, i.e.![]() .
.
Sometimes it happens, that even at k = 1, we obtain desired results. For example, a value of
![]() is a whole number, i.e. 19 is a prime number after 17. In addition,
is a whole number, i.e. 19 is a prime number after 17. In addition,
the numbers 17 and 19 are twins.
Some answers to the posed problem for a small set of primary prime numbers are given as Table 1. In this table, n is a counting number of a prime number.
In short, if there is a set of primary prime numbers, then while using expression of Equation (1) it is always possible to find the next prime number.
To show diversity to the proposed method, we offer one more elegant algorithm, the essence of which is primarily to find a value of k through existing prime numbers.
For this, we use Chinese remainder theorem, which states: “If natural numbers ![]() are coprimes in pairs, then for any whole numbers
are coprimes in pairs, then for any whole numbers ![]() such that
such that ![]() for all
for all ![]() there is a number N, which when divided by
there is a number N, which when divided by ![]() gives a reminder
gives a reminder ![]() for all
for all![]() .” [2] .
.” [2] .
It is known that constructive method for proving this theorem allows to solve the following system of linear equations modulo [3] [4] :
![]() (2)
(2)
![]()
Table 1. Using with proposed theorem found primes number.
![]()
If sets (![]() ) и (
) и (![]() ) fulfill conditions of Chinese theorem, then solution for system of Equations (2) exists and is unique within the accuracy of an operation by modulo
) fulfill conditions of Chinese theorem, then solution for system of Equations (2) exists and is unique within the accuracy of an operation by modulo![]() , and this solution looks like [2] -[4] :
, and this solution looks like [2] -[4] :
![]() (3)
(3)
where ![]() (4)
(4)
![]() (5)
(5)
i.e. ![]() is inverse for
is inverse for ![]() by module
by module![]() .
.
Now, knowing the solution of Equation (3) we can easily find the values of factor k. It is obvious, that Chinese theorem is true for any sequence of prime numbers since prime numbers are always coprimes in pairs. Then, considering for ![]() in the system of Equation (2) a sequence of prime numbers, for our case we obtain that
in the system of Equation (2) a sequence of prime numbers, for our case we obtain that
![]() . (6)
. (6)
Now, by combining the proposed theorem with Chinese theorem, we have from Equations (1)-(6):
![]() (7)
(7)
Expression of Equation (7) shows that if a sequence of prime numbers is known, we are always able to calculate a value of k in advance. Then, by substituting of calculated value of k in Equation (1), we verify the fulfillment of the conditions of Equations (1a) and (1b). If these conditions are not fulfilled, then a number considered as ![]() is not a prime number. This number is the next composite number that stands for the prime number
is not a prime number. This number is the next composite number that stands for the prime number![]() . And, if the conditions of Equations (1a) and (1b) are met, then
. And, if the conditions of Equations (1a) and (1b) are met, then ![]() is a desired prime number. After that, we proceed with finding next prime
is a desired prime number. After that, we proceed with finding next prime ![]() and the cycle repeats.
and the cycle repeats.
In this case algorithm for searching prime numbers in odd numbers series looks as follows.
Step 1. Input values of existing prime numbers![]() , where
, where![]() , etc.
, etc.
Step 2. For![]() , we input an odd number, which in a line of odd numbers follows a prime number
, we input an odd number, which in a line of odd numbers follows a prime number![]() . Here
. Here![]() , where
, where ![]() In this case for 1st step
In this case for 1st step![]() .
.
Step 3. Calculate ![]() and
and![]() .
.
Step 4. Calculate ![]() for all
for all![]() .
.
Step 5. Using extended Euclid’s algorithm, we find ![]() for all
for all ![]() from the condition
from the condition ![]()
![]()
Table 2. Comparison results between Wilson’s theorem and proposed theorem.
Step 6. Calculate the desired value of k by the formula:
![]()
Step 7. Check fulfillment of equality (1).
Step 8. Conditional operator works here.
-If conditions of Equations (1a) and (1b) are not met, then considered number ![]() is not a prime number, then assign m = m + 1 and proceed to step 2. The cycle repeats until conditions of Equations (1a) and (1b) will not be met.
is not a prime number, then assign m = m + 1 and proceed to step 2. The cycle repeats until conditions of Equations (1a) and (1b) will not be met.
-If conditions of Equations (1a) and (1b) are fulfilled, then ![]() is a desired prime number, followed a prime number
is a desired prime number, followed a prime number![]() .
.
Step 9. Generation of the next prime number ![]() is carried out similarly.
is carried out similarly.
The cycle repeats.
We assume that the process of generating prime numbers based on the proposed theorem is faster than a generation based on Wilson’s theorem.
In case of Wilson’s theorem it is quite difficult to calculate the factorial of (n − 1)!. In fact, if generation is carried out in the area of the large numbers, then calculation of given factorial creates significant difficulties. This is explained by the fact that there are intervals in the sequence of natural numbers which include thousands, millions, billions and even some arbitrarily large number of natural numbers standing in a row, among which there is no prime number. For example, if you set an arbitrary large natural number m, let build a series of numbers ![]() then it is obvious that each of these numbers is a composite number. You can easily check, particularly m! + 2 is evenly divided by 2, m! + 3 is divided by 3, and + is evenly divided by m, i.e. there is no a prime number in the large interval of
then it is obvious that each of these numbers is a composite number. You can easily check, particularly m! + 2 is evenly divided by 2, m! + 3 is divided by 3, and + is evenly divided by m, i.e. there is no a prime number in the large interval of![]() . If, for example, m = 1010, then in case of Wilson’s theorem, calculation of the factorial will inevitably lead to a large number of calculations involving a huge amount of large composite numbers. And in case of the proposed theorem calculations are mainly made with prime numbers.
. If, for example, m = 1010, then in case of Wilson’s theorem, calculation of the factorial will inevitably lead to a large number of calculations involving a huge amount of large composite numbers. And in case of the proposed theorem calculations are mainly made with prime numbers.
This is clearly illustrated from Table 2, which shows results of searching prime numbers using methods following from Wilson’s theorem (left part of the table) and proposed theorem (right part of the table).
The left part of the table provides calculations made for values of from 2 to 41. In the 1st column of left part of the table (case of Wilson’s theorem) all natural numbers are given. In this column cells containing prime numbers which are green highlighted for illustrative purposes. In the 2nd column the calculated values of ![]() factorial are shown. And 3rd column provides remainders which take zero values in case of prime numbers.
factorial are shown. And 3rd column provides remainders which take zero values in case of prime numbers.
Similar results, obtained using proposed theorem, are shown in the right part of the table. First column of the right part shows prime numbers. Second column of this part presents calculated values of![]() . And the last column shows values of remainders which also take zero values for prime numbers.
. And the last column shows values of remainders which also take zero values for prime numbers.
Table 2 shows that, in case of Wilson’s theorem, in order to carry out generation of prime numbers at least up to 13th prime number, i.e. up to ![]() it is necessary to perform a lot of laborious calculations with large numbers.
it is necessary to perform a lot of laborious calculations with large numbers.
A right part of the table shows only those numbers with which the calculations have been made using the proposed method. Comparing the left and right parts of the table, we can see that efficiency, speed, and convenience of the proposed method are beyond question, this is obvious. Plus, for a set of large integers, this obviousness becomes even more than self-evident.
Note again that in case of Wilson’s theorem the complexity lies in calculation of ![]() factorial. It is easier to calculate
factorial. It is easier to calculate![]() ; therefore elementary tests, determining whether a number is prime number, are based on Fermat’s theorem, rather than on Wilson’s theorem. However, note that in contrast to Fermat’s small theorem, Wilson’s theorem simultaneously is a necessary and sufficient condition for determining primality of any number.
; therefore elementary tests, determining whether a number is prime number, are based on Fermat’s theorem, rather than on Wilson’s theorem. However, note that in contrast to Fermat’s small theorem, Wilson’s theorem simultaneously is a necessary and sufficient condition for determining primality of any number.
References