Rays’ Change of Directions between Inertial Frames and Stellar Aberration

Caesar P. Viazminsky¹, Piere K. Vizminiska²

¹Department of Physics, Illinois Institute of Technology, Chicago, IL, USA.
²Department of Computer Engineering, University of Detroit Mercy, MI, USA.

DOI: 10.4236/am.2015.69138                

Abstract

The path of a light’s signal is one and the same in the universal space regardless of the inertial frame by which it is identified. However, only one frame can be taken stationary and identified with the universal space while all other frames are moving. The direction of the path of a light’s pulse in a moving frame is determined in terms of its direction in the stationary one; the result is utilized to explain stellar aberration and show that the tilted direction in the moving frame depends only on its velocity. The aberration increment vector is introduced and employed to determine the apparent position of a star at each point of the earth orbit. Aberration in an earth satellite relative to the geocentric frame is presented. The direction’s change of a light beam between graded inertial frames promotes explaining aberration in an earth’s satellite in parallel to stellar aberration on earth.

Keywords

Direction’s Change of Light Rays, Stellar Aberration, Aberration in a Satellite, Aberration Increment, Graded Inertial Frames

1. Introduction

In earlier works [1] [2] the fundamentals of the theory of universal space and time (UST) were presented. According to the UST, time intervals in an inertial frame S are essentially measured by corresponding spatial intervals travelled by light signals. Equivalently, the geometric distance 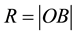between two points B and O in S is measurable by the time duration 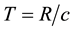(or geometric time) of a light trip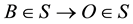, which is the same as the duration of the light trip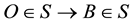. The latter simple relation which is valid only when B and O are stationary in S, puts geometric time and length on equal footing as equivalent measures of the same distance. The physical, or universal space, can be identified by one arbitrary inertial frame S (or s), which is considered stationary while any other inertial frame s (S) is moving relative to S (s); and a light’s trip thus follows the same path in the universal space whether identified by S or s [1] .

The light path is seen in the moving frame tilted from its direction in the stationary frame by the aberration angle. In the heliocentric frame the direction of the earth’s velocity, due to its orbital motion, keeps changing, resulting in every received starlight continuously changing its direction in the geocentric frame. The latter fact is manifested in a periodic change in the apparent position of distant stars throughout the year. The phenomenon of the annual apparent motion of celestial objects about their locations, named stellar aberration, was discovered by Bradley in 1727 [3] [4] , who also explained it employing the corpuscular model of light [3] [5] . One can also account for aberration in terms of light’s waves traveling through the ether, provided the ether remains completely undisturbed by the earth’s motion [6] . Bradley’s explanation of stellar aberration however, proved inadequate since it couldn’t account for the negative results of Airy Experiment [4] .

The following items summarize the goals that we seek in this work and the plan of its presentation.

Ÿ We start by an outline of the structure and relevant results of UST theory.

Ÿ Find the relation between the path of a light’s pulse in the stationary and moving frames.

Ÿ Utilize the relation that we found to explain the aberration phenomenon and obtain a new expression for stellar aberration angle. Although different from Bradley’s and the relativistic expressions, our formula is in accord with experiment results and it determines the aberration angle at each instant of the year.

Ÿ The concepts of the aberration increment and aberrated vector are introduced and used to determine the apparent motion of a given star and the direction at which the telescope should be pointed at various times of the year.

Ÿ The direction’s change of light beams between graded inertial frame is introduced and employed to quantify aberration in an earth’s satellite.

Basics and discussions of stellar aberration can be found in many textbooks and articles [3] -[8] .

2. Universal Direction of a Light’s Ray

Let S be an inertial frame in which a source of light b is moving at a constant velocity u, and s be another inertial frame in standard configuration with S and co-moving with b. We found in [1] that a pulse of light emanating from 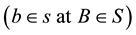and received by the conjugate observers follows the same path in the universal space whether identified by S or s. The pulse’s path is realized within each frame, S or s when considered stationary, as propagating along the same vector which is identified by 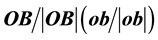when S (s) is the stationary frame [1] , i.e.

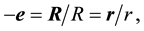(2.1)

where R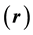 is the geometric radius vector of the point (b at B) in S (in s) when stationary. The relation (2.1) implies that the direction of the radius vector of (b at B) as measured within the stationary frame, S or s, is the same one thing. If e is specified in a basis of unit vectors of S or s (when stationary) then the directional angles are the same in both frames [1] :

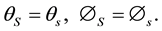(2.2)

This shows that no matter was the magnitude of the source’s velocity in S, or equivalently, regardless of the frame S in which the source b was viewed, the direction of the light’s path as observed within S is identical to its direction as observed within the frame s in which the source b is stationary (the word “within” here implies that the frame concerned is considered stationary). This means that all observers conjugate to o, each within his frame, are in accord with the direction’s measurements obtained by o, and consequently with each other. Therefore, the direction of the path of a light’s pulse, as measured within each inertial frame, is independent of the relative velocity between the source and the receiver; the same values of the directional angles are obtained by all inertial conjugate observers, each within his inertial frame (Figure 1). The latter statements manifest the absolute character of the path direction of light.

In the rest of this section we brief some basic concepts and results of UST that is relevant to our current work.

Suppose that at an instant, corresponding to occupying the point, light emanates from

. The light arrives at (and hence at the contiguous observer) at an instant t. Assuming that the geometric time distance between and is, then the pulse arrives at O (and o) at an instant t related to the geometric time T by the scaling transformation [2] :

(2.3)

where,. The factor is called the scaling factor.

It was shown [1] [2] that when the pulse arrives at O, i.e. at the instant t, the moving object b occupies a position at distances and from B and O respectively, where (Figure 2(b)). The pulse follows the path in S and a path in s connecting the present position of b with o, but since the frame s is moving in S the latter path is identified by in S, where is the unit vector of. I.e. in the moving frame s light follows the path.

Note that if the pulse emanates from B, then as before, the pulse follow in S and in s. In both case we have, or, which can be written as

(2.4)

Taking the cross product of both sides with we obtain, which gives, where. Dividing Equation (2.4) by t and employing (2.3) we get

Figure 1. The pulse follows one and the same path (in red) in the universal space whether identified by S or s.

(a) (b)

Figure 2. (a) The pulse path is in s and in S when s is stationary; (b) The pulse path is in S and in s when S is stationary.

(2.5)

or

(2.6)

where

(2.7)

is the Euclidean factor [2] .

In the UST theory, time is an absolute entity and hence the duration of a light trip is the same in all inertial frames, but its direction and spatial length may differ. Therefore, if S is the universal frame, the duration of the trip in both frames (S and s) is t, whereas T is its geometric time length in S. If B is the source of light, then T is the duration of the trip in both frames and of course it is geometric length in S. In both cases, is the spatial length of the concerned trip as viewed in the moving frame s.

If the frame s is chosen the universal frame (stationary), then in the first case the time duration of the trip is t in both frames, and its geometric length in s is ct. If B is the source of light then the duration of the trip is T in both frames. The geometric length of both trips (of course in s) is ct. The length of the second trip in s is (Figure 2(a)).

In parallel to the relations (2, 4 - 6) we have when s is stationary

(2.8)

(2.9)

(2.10a)

or

(2.10b)

which all are obtained through replacing by and by (or by). In (2.10b) we utilize the fact that which results from (2.7) and [1] . Crossing both sides of any relation (2.8 - 10) by yields which determines the angle between the pulse path as seen in S and s. As it should be, the same angle occurs whether the pulse emerges from b at B or from B at b; however, the first (second) angle is realized when S (s) is the universal frame.

3. The Ray’s Direction in a Moving Frame―Aberration Angle

Consider a parallel beam of light propagating in the universal frame S parallel to the direction. The path of a narrow beam (say a ray) is determined in S by two points we assume the ray propagates in the direction. Let M be an inertial frame in standard configuration with S and moving at a velocity in S. The question is, how is the vector BO seen in M?

The path of the ray in M is also determined by two points in M. Let m be a point in M and assume that when at a pulse of light emanates from. The pulse is received by a point in M that is contiguous to, call it. When the pulse arrives at (and) the point occupies the position. Therefore, in the moving frame M the beam is seen propagating along. In down to earth language, the whole situation will not change if we envisage the beam (or the directed segment BO) as a thin straight tube through which a liquid, or a current of any nature, flows down (from B to O) at any velocity; the tube is seen tilted in M to the position. According to Section 2 the sides of the triangle are

(3.1)

Thus the direction of the ray is observed in M tilted from a fixed direction in the universal space S by an angle determined by

which yields

(3.5)

where is the angle between the vector velocity of m, or the velocity of the moving frame M, and the fixed direction (Figure 3). The angle is called the aberration angle. The velocity of M in S, the fixed direction in S, and the tilted direction all lie in a plane called the aberration plane. The tilted direction in S is obtained through tilting the fixed direction OB in S in the aberration plane towards the vector velocity of M by the aberration angle.

The source of light b (a star for instance) can be seen by a telescope, with ocular and objective lenses r and o respectively, only if the telescope ro is set along the direction, which amounts to tilt the telescope from the fixed direction, in the aberration plane, by the aberration angle in the direction of the motion (Figure 4).

4. Stellar Aberration

Consider a “distant” star b, in the sense that the radius of the earth’s orbit is negligible in comparison with the distance between the star and the sun. In this context, the phrase “the vicinity of the sun at some instant” will mean the region of space containing the sun and the earth and whose dimensions remain negligible in comparison with the distance of b from the sun throughout a long period of time. In the stationary inertial frame with origin at the sun “N”, the motion of b, as seen from the vicinity of N, has no observable effect on its location in S during a relatively long period of time (centuries), and in particular, on the latitude angle, between and the ecliptic, which remains almost unchanged. Rays from b received by all S observers in vicinity of the sun are practically parallel, and the star b appears to all these observers at the same altitude. Let be a reference frame co-moving with the earth in its orbital motion, and whose axes remain parallel to the axes of the inertial frame S. i.e. geocentric frame.

All S-observers (in vicinity of the sun) see the rays from the star b throughout the year coming along the

Figure 3. The same beam is seen along OB in S and in the moving frame M.

Figure 4. In order to see the star b, a telescope in M with ocular o must points along om'.

negative direction of the vector which is the unit vector of. For a geocentric observer, which is moving around the sun, the direction of the ray received is tilted from its direction in S in the momentary aberration plane by the aberration angle, where

(4.1)

and is the angle between the fixed direction in S and the momentary orbital velocity of the Earth around the sun. Therefore, a star b is seeable by terrestrial telescope ro only if it is tilted in the aberration plane from the fixed direction in S by the aberration angle.

The vector velocity of the earth around the sun, with is the unit tangent vector to the earth’s orbit, rotates approximately uniformly in S and in the geocentric frame M, with an angular velocity. There follows that the aberration plane containing this rotating vector, the fixed direction, and the tilted direction ro, rotates about Nb in S and about Eb in M with angular velocity. We choose the axes of S so that the Z axis is perpendicular to the ecliptic and the star b is the XZ plane. The zero of timing is chosen to correspond to the closest position of the earth to the star, i.e. when earth is on the X-axis, and thus its velocity is perpendicular to the XZ plane. In either frame, S or M, and within the approximations imposed by the meaning of “distant star”, the unit vector of the negative direction of the incoming ray and the tangent vector of the earth orbit are (Figure 5)

(4.2a)

(4.2b)

where we assume in writing (4.2b) that the earth orbit is approximately circular. The cosine of the angle between the earth’s vector velocity and the negative direction of the incoming ray is

(4.3)

Identifying by, we get from (4.1)

(4.4)

where is the polar angle in the ecliptic of the radius vector connecting the sun N and the earth E, i.e.,. For a given star the altitude angle is fixed, and the relation (4.4) determines the

Figure 5. Because the star b is too far, Nb and Eb are essentially parallel. The true position of b is along the same direction in the heliocentric and geocentric frames S and M.

aberration angle in terms the polar angle of the earth’s position at its orbit in the ecliptic, or equivalently, at any instant throughout the year. The angle between two lines of sight separated be six months period is

(4.5)

By (4.5) the aberration angle attains its maximal values

(4.6)

for, which corresponds to, and its minimal values

(4.7)

for.

Substituting for v and c in (4.6) by and we obtain the value for the aberration constant, which is about far from the generally accepted value. Recall that we obtained our value for on assuming that the earth orbit is circular, while in reality the eccentricity of the elliptical earth orbit varies in cycle extending to hundreds thousands of years [9] from 0.0034 to 0.058; it is currently 0.0167. Provided the orbits are approximately circular, the aberration constants and for another planet p are related by

(4.8)

where are the planet’s (the earth’s) velocity and distance from the sun.

Recalling that the telescope in s is tilted by towards the earth’s orbital velocity vector, the observed alti-

tude of the star is highest for and lowest for. The altitude of the star at or

remains unchanged because the telescope is tilted horizontally (by).

Two Special Cases: (i) For, which corresponds to the line of sight to the star b is perpendicular to the ecliptic, we have, and both Equations (4.1) and (4.4) reduce to.

(ii) The distant star b is in the ecliptic: Setting in (4.4) we obtain

(4.9)

The aberration occurs in the ecliptic attaining its maximal absolute value (4.6) at and vanishes

for i.e. the maximum value occurs when the line of sight to the star is perpendicular to

the earth’s velocity and minimum when the earth directly approach the star or recedes from it.

5. The Aberration Increment and Aberration Direction

The aberrated direction is the momentary direction along which the star is seen from Earth. Being in the aberration plane, its unit vector is a linear combination of the fixed direction and the unit Earth’s velocity. The aberration increment is of length given by (4.5), lies in the aberration plane, and makes an acute angle with earth’s velocity. In the bases of the unit vectors of the frame we have

(5.1)

Since is small, the aberration increment can be considered perpendicular to the fixed direction of the star; it is specified by determining the parameters and so that and. Utilizing (4.5) we get and hence

(5.2)

The aberration vector is what should be added to the direction to obtain the aberrated direction along which the star is seen in M. The aberrated direction A is normalized to the second order in, for, In order to see the star, a telescope of length l should be pointing to represent the vector.

Two particular independent directions of correspond to the following cases:

(i) At we have

(5.3)

which shows that, when the Earth’s velocity is perpendicular to the line of sight to b, the telescope is tilted horizontally in the direction of motion by.

(ii) For we have

(5.4)

As the z-component is positive for and negative for, the telescope is tilted upward at the first place and downward at the second.

It is convenient to decompose the aberration increment into a horizontal (east-west) and “vertical” (north- south) components, , where

(5.5)

It is clear that the triad is orthogonal (whenever are not zero). The vector can be written in the form

(5.6)

where f is a unit vector defined by the quantity in the parentheses. It is clear that f is perpendicular to and j and is an orthonormal proper basis. The horizontal and vertical aberration increments at each instant of the year are summed up by the formula

(5.7)

From the parametric representation the aberration increment displays the ellipse

(5.8)

Likewise, the aberrated vector draws the same ellipse.

Aberration in Graded Inertial Frames:

When S and M are equally inertial the star is seen in each frame when taken universal along the same direction. If S(M) is universal, which implies that the other frame is moving, the line of sight to the star in M (S) is tilted from by the aberration angle.

The aberrated direction in the geocentric frame M is determined with reference to a fixed direction in the heliocentric frame S. But it is known [10] [11] that our sun is revolving about the center of the galaxy at about 8 times the earth’s orbital velocity and making a full round in about 230 million years (a galactic year) [10] [11] . As observed from the sun, the aberration increment vector concerning a extragalactic object is given by an equation like (5.2) in which v is replaced by 8v and The aberrated vector of an extragalactic object traces during a galactic year an ellipse that is 8 times larger in both dimensions (which amounts to v replaced by 8v in (5.8)). The aberrated vector A which points to the apparent position of the extragalactic object in the heliocentric frame S is practically fixed at a direction for thousands of years, and the annual aberration (observed from the earth) determines the apparent position of the extragalactic object relative to (symbolized earlier by).

In reality no frame is exactly inertial, but there are graded inertial frames in which one frame is more inertial than another. For instance, the set of non-rotating frames with origins at the center of mass of, the galaxy (G), the solar system (S), the earth-moon system (M), an earth satellite, is graded. Indeed, the motion of S can be counted uniform for thousands of years, whereas the duration of uniformity of earth’s motion in S ranges from minutes to hours depending on the required degree of accuracy. The apparent position of a celestial object b in the heliocentric frame S works as a true fixed direction to which is referred the apparent position of the same object b in M. Moreover, the apparent position in M can be considered for few hours as a constant position to which we refer the apparent position of b in an Earth’s satellite. The deviation of the motion of a frame from uniformity during the period at which it is taken inertial is either undetectable, or its effect on the results of the experiment is negligible.

6. Observing Aberration from an Earth’s Satellite

Suppose that a satellite is orbiting the earth in a low circular orbit that lies in the ecliptic. During the orbital period of the satellite, say, the geocentric frame is almost stationary, and the position of our distant star b appears fixed in M. This defines an approximately fixed direction (or) in M along which the star b is seen for two hours. Now, an argument parallel to that presented in section 4 can be carried out here, with the earth replacing the sun and the satellite replacing the earth, leading to an aberration angle in the satellite frame given by

(6.1)

where is the orbital velocity of the satellite relative to and is the angle between the negative direction of the incoming ray and the momentary vector velocity of the satellite in M. Equation (6.1) can be written in the form

(6.2)

where is the satellite’s angular velocity, , and the zero of time is chosen when the satellite is in the plane. After half a period the velocity of the satellite in M reverses direction, with it the aberration angle, resulting in an angle between the two lines of sight from the satellite to b separated by half a period. The latter takes its maximum (the satellite aberration constant) when measured for

and its minimum when measured for Since for and, the constant of aberration for a satellite with velocity is.

The apparent motion of the star b repeats itself once a year when observed from the earth, and times per a year when observed from our satellite. The repetition in the second case is quasi-periodic, in the sense that it holds about a varying fixed direction. The first apparent motion is approximately periodic throughout centuries or perhaps thousands of years.

7. Conclusion

The UST theory provides a neat explanation of the stellar aberration phenomenon that highlights its independence from the velocity of the light source. By introducing the concept of the aberration increment vector we were able to find an approximate formula for the apparent position of the celestial object at each moment of the year. The concept of graded inertial frames makes it clear why annual stellar aberration depends only on the velocity of the earth relative to the heliocentric frame. Employing the same concept enables us to treat aberration when observed from a satellite in parallel to its treatment when observed from the earth.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Viazminsky, C.P. and Vizminiska, P.K. (2014) On Universal Space and Time. Applied Mathematics, 5, 2530-2546. http://dx.doi.org/10.4236/am.2014.516243
[2]	Viazminsky, C.P. and Vizminiska, P.K. (2014) On Universal Mechanics and Superluminal Velocities. Applied Mathematics, 5, 2728-2738. http://dx.doi.org/10.4236/am.2014.517260
[3]	Bradley, J. (1728) Account on a New Discovered Motion of the Fix’d (Fixed) Stars. Philosophical Transactions of the Royal Society of London, 35, 637-660. http://dx.doi.org/10.1098/rstl.1727.0064
[4]	French, A.P. (1968) Special Relativity. Butler & Tanner Ltd., Frome and London, Ch. 2 & 3.
[5]	Russo, D. (2007) Stellar Aberration: The Contradiction between Einstein and Bradley. Apeiron, 14, 95-112.
[6]	Stokes, G.G. (1845) On the Aberration of Light. Philosophical Magazine, 27, 9-15.
[7]	Phipps Jr., T.E. (2005) Testing Relativity for One-Way Light Propagation. Apeiron, 12, 136-143.
[8]	Rindler, W. (1977) Essential Relativity. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-3-642-86650-0
[9]	http://www.britannica.com/topic/constant-of-aberration
[10]	http://www.thefullwiki.org/Aberration_of_light
[11]	https://en.wikipedia.org/wiki/Aberration_of_light