Heat and Mass Transfer of Upper Convected Maxwell Fluid Flow with Variable Thermo-Physical Properties over a Horizontal Melting Surface ()
1. Introduction
Mass transfer can be described as the movement of mass (material) through a fluid-fluid interface or a fluid-solid interface. The term “mass transfer” is commonly used in engineering and in industry for physical processes that involve diffusive and convective transport of chemical species within physical systems. The three kinds of fluxes in relation to mass transfer have been explained in Asano [1] ; Mass flux can be expressed as the addition of diffusional flux and convective mass flux. The analysis, description, theoretical and experimental studies of boundary layer flow together with heat and mass transfer across incompressible fluid as it flows over ahorizontal surface has gained attention of many researchers. In addition, series of investigations have been carried out towards the understanding of the dynamics of viscoelastic material since the contribution of James Clerk Maxwell in 1867 to the body of knowledge. The dynamics of material having the properties of elasticity and viscosity when undergoing deformation is a fundamental topic in fluid dynamics. This kind of material referred to as “Maxwell fluid” has attracted the attention of many researchers due to its wide industrial and technical applications. James Clerk Maxwell proposed Maxwell fluid in 1867 and the knowledge was popularized by James G. Oldroyd few years after (for details see Christopher [2] ). The Upper Convected Maxwell model can be described as the generalization of the Maxwell material for the case of large deformation using the upper- convected time derivative (also known as Oldyrold derivative) which is the rate of change of some tensor properties of a small parcel of fluid that is written in the coordinate system stretching with the fluid. It is worth noticing that mathematical model of Upper Convected Maxwell has been described (or defined) as a function of stress tensor, relaxation time, upper convected time derivative of stress tensor, fluid velocity, material viscosity at steady simple shear and tensor of the deformation rate.
It is a common known fact in rheology that given enough time, even a solid-like material will flow (see Barnes et al. [3] ). In view of this, it is required to characterize the fluidity of materials under specific flow conditions (i.e. adimensionless number that incorporates both the elasticity and viscosity of material is required). Steffe [4] reported that Deborah number which is defined as a ratio of stress relaxation time (i.e. time it takes for a material to adjust) to applied stresses (deformations) was proposed by Eugene C. Bingham and Markus Reiner. Recently, Poole [5] reported the history behind the given name “Deborah” according to Reiner [6] as a ratio of time of relaxation to time of observation. In view of this, Sadeghy et al. [7] investigated Sakiad is flow of a UCM fluid. The role played by a fluid’s elasticity on the characteristics of its Sakiadis flow was analyzed. In the same context, it was reported that at high Deborah number, UCM flow corresponds to solid-like behavior and low Deborah numbers to fluid-like behavior. Recently, Shateyi et al. [8] investigated entropy generation on a magnetohydrodynamic flow and heat transfer of a Maxwell fluid over a stretching sheet in a Darcian porous medium. In the article, a new numerical scheme (Chebyshev Spectral Collocation Method) is adopted to solve nonlinear systems of boundary value problems. Considering some rheological complex fluids such as polymer solutions, blood, ice creams and synovia fluid, Abbas et al. [9] argued that the second-grade fluid model adopted in the work of Fosdick and Rajagopal [10] does not give reasonable results for flows of highly elastic fluids (polymer melts) that occur at high Deborah number. Forsuch situations the Upper Convected Maxwell (UCM) model is quite appropriate. Using the UCM model, MHD boundary layer flow of a UCM fluid in a rectangular porous channel was successfully investigated. The study on dynamics of Upper Convected Maxwell fluid is extended in Hayat et al. [11] and reported that boundary layer thickness decreases by increasing the magnitude of MHD parameter, suction/injection velocity parameter and relaxation time parameter. In recent years, many researchers has investigated and reported the effect of some parameters on Upper Convected Maxwell fluid flow [12] - [22] .
Internal energy generation can be explained as a scientific method of generating heat energy within a body by chemical, electrical or nuclear process. Natural convection induced by internal heat generation is a common phenomenon in nature. Crepeau and Clarksean [23] have reported a similarity solution of a fluid problem along a vertical plate with constant temperature in the presence of an exponential decaying heat generation term under the assumption that the fluid has an internal volumetric heat generation. In many situations, there may be appreciable temperature difference between the surface and the ambient fluid. This necessitates the consideration of temperature dependent heat source(s) that may exert a strong influence on the heat transfer characteristics (see Salem and El-Aziz [24] ). Salem and El-Aziz [25] further stated that exact modeling of internal heat generation or absorption is quite difficult and argued that some simple mathematical models can express its average behavior for most physical situations. Recently, Animasaun et al. [26] reported that when the plastic dynamic viscosity and thermal conductivity of non-Newtonian Casson fluid are considered as temperature dependent, exponentially decaying internal heat generation parameter is an important dimensionless number that can be used to increase velocity and temperature of the fluid as it flows. Effect of this internally generated heat energy on the
surface may lead to melting of solid surface. From the knowledge of kinetic theory of matter, some solids may melt if expose to a high temperature. In an earlier study, the effect of melting on heat transfer was studied by Yin-Chao and Tien [27] for the Leveque problem. The tangential velocity profile is assumed to be linear. It was further reported by Tien and Yen [28] that the approximation in [27] is valid if one deals with a high Prandtl number fluid so that the significant temperature change takes place only within a thin layer of fluid immediately adjacent to the solid boundary and consequently the velocity profile inside this thin layer can be approximated by a linear segment. The similarity between the melting problems and mass transfer or transpiration cooling problems is further explained in [28] . In addition, effect of melting on heat transfer between melting body and surrounding fluid qualitatively from the point of view of boundary layer theory was investigated. This contribution to the existing knowledge attracted Epstein [29] to present a note on a systematic method of calculating steady state melting rates in all circumstances involving the melting of solid bodies immersed in streams of warmer fluid of the same material. In the same context, relationship between boundary condition of evaporation and that of melting is discussed. In recent years, many researchers have investigated and reported the effect of melting parameters; for details see [30] - [32] .
In all of the above mentioned studies, fluid viscosity and thermal conductivity have been assumed to be constant function of temperature within the boundary layer. However, it is known that physical properties of the fluid may change significantly when expose to internal generated temperature. For lubricating fluids, heat generated by the internal friction and the corresponding rise in temperature affect the viscosity of the fluid and so the fluid viscosity can no longer be assumed constant. In a case of melting as reported by many researchers [30] - [33] , it is worth mentioning that temperature of fluid layers at free stream may also have significant effect on the intermolecular forces of upper convected Maxwell fluid. The increase of temperature may also leads to a local increase in the transport phenomena by reducing the viscosity across the momentum boundary layer and so the heat transfer rate at the wall may also be affected greatly. According to Batchelor [34] , Animasaun [35] and Meyers et al. [36] , it is a well-known fact that properties which are most sensitive to temperature rise are viscosity and thermal conductivity. Recently, Mukhopadhyay [37] considered this same fact in order to explain stagnation point flow behavior on non-melting surface while Animasaun [38] adopted the model and reported the dynamics of unsteady magnetohydrodynamic convective fluid flow with radiation and thermophoresis of particles past a vertical porous plate moving through a binary mixture in an optically thin environment. Motivated by all the works mentioned above, it is of interest to contribute to the body of knowledge by studying the dynamics of upper-convected Maxwell fluid flow considering a case in which the influence of temperature on viscosity and thermal conductivity is properly accounted for. In this study, we aim at investigating the motion of UCM fluid flow over a melting surface; considering a case in which the flow is subjected to thermal and solutal stratification. This is achieved by modifying and incorporating all the necessary term (s) into the boundary layer equation in line with boundary layer theory, heat and mass transfer theory. Lastly, to extend the research of Hayat et al. [39] , Mustafa et al. [17] , Pop et al. [30] , and Prasad et al. [21] .
2. Mathematical Formulation
We consider steady and incompressible Upper Convected Maxwell (UCM) fluid flow with variable thermo- physical properties over a melting surface situated in hot environment. The flow under consideration is assumed to occupy the domain 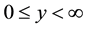 as shown in Figure 1. Boundary layer equations which best describe Upper Convected Maxwell fluid flow can be derived starting from Cauchy equations of motion. Following (Dunn and Rajagopal [40] and Sadeghy et al. [7] ), steady two-dimensional fluid flow can be written as
as shown in Figure 1. Boundary layer equations which best describe Upper Convected Maxwell fluid flow can be derived starting from Cauchy equations of motion. Following (Dunn and Rajagopal [40] and Sadeghy et al. [7] ), steady two-dimensional fluid flow can be written as
 (1)
(1)
 (2)
(2)
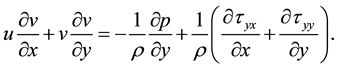 (3)
(3)
where 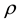 is the density of the steady Upper Convected Maxwell fluid. Poole [5] explained that in steady simples hear flow (SSSF), the dominant elastic force will be due to the first normal-stress difference (
is the density of the steady Upper Convected Maxwell fluid. Poole [5] explained that in steady simples hear flow (SSSF), the dominant elastic force will be due to the first normal-stress difference (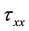 ,
, ) and the viscous force is simply the shear stress (
) and the viscous force is simply the shear stress ( ).
).
In Equation (2) and Equation (3), elastic terms are 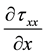 and
and . The viscous terms are
. The viscous terms are 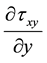 and
and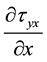 .
.
Using order of magnitude as introduced by Ludwig Prandtl and stated in Schichting [41] , it is valid to say that
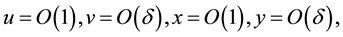 (4)
(4)
and easy to show that in Equations (2) and (3), order of magnitude of the two elastic terms and order of magnitude of the two viscous terms are the same if
 (5)
(5)
This condition can be explained following Sadeghy et al. [7] . Elastic effects should be considered in aboundary layer only for those viscoelastic fluids for which  is of an order larger than
is of an order larger than ![]() and
and![]() . Not all viscoelastic fluid models can meet such a strong restrictive condition. Assuming that a fluid can be found for which the order estimates as given by Equation (5) really hold; the stress components of a UCM fluid can indeed be represented by the above order estimates justifying the use of such a model in the present work. The equations of motions can be simplified to
. Not all viscoelastic fluid models can meet such a strong restrictive condition. Assuming that a fluid can be found for which the order estimates as given by Equation (5) really hold; the stress components of a UCM fluid can indeed be represented by the above order estimates justifying the use of such a model in the present work. The equations of motions can be simplified to
![]() (6)
(6)
![]() (7)
(7)
In the presence of pressure gradient, the equations of motions together with continuity equation can be written as
![]() (8)
(8)
![]() (9)
(9)
In Equation (8) and Equation (9), there exist five unknowns (i.e. five dependent variables) which are u, v, ![]() and
and![]() . In order to resolve this (i.e. to make the number of unknowns equal to the number of equations), a constitutive equation relating stress components to the deformation field is needed. For a Maxwell fluid, the stress tensor
. In order to resolve this (i.e. to make the number of unknowns equal to the number of equations), a constitutive equation relating stress components to the deformation field is needed. For a Maxwell fluid, the stress tensor ![]() can be related to the deformation-rate tensor
can be related to the deformation-rate tensor ![]() as stated in Larson [42] and Sadeghy et al. [7] as
as stated in Larson [42] and Sadeghy et al. [7] as
![]() (10)
(10)
The time derivative ![]() appearing in Equation (10) is the so-called Upper Convected time derivative which
appearing in Equation (10) is the so-called Upper Convected time derivative which
has been devised to satisfy the requirements of continuum mechanics (i.e., material objectivity and frame in difference; see Larson [42] ) and ![]() is known as zero-shear rate viscosity. This time derivative, when applied to the stress tensor, reads as follows
is known as zero-shear rate viscosity. This time derivative, when applied to the stress tensor, reads as follows
![]() (11)
(11)
In Equation (11), ![]() is the velocity gradient tensor. The Bernoulli equation for the free stream flow just above the boundary layer where there is no viscous shear is defined as
is the velocity gradient tensor. The Bernoulli equation for the free stream flow just above the boundary layer where there is no viscous shear is defined as
![]()
This can be differentiated and used to eliminate the pressure gradient Lienhard-IV and Lienhard-V [43]
![]()
Since the flow is along flat horizontal melting plate, ![]() and
and ![]() are constant. For an incompressible fluid obeying upper convected Maxwell model with temperature dependent dynamics viscosity and thermal conductivity, the
are constant. For an incompressible fluid obeying upper convected Maxwell model with temperature dependent dynamics viscosity and thermal conductivity, the ![]() momentum equation and the energy equation can be simplified using the usual boundary layer theory approximations and then obtain
momentum equation and the energy equation can be simplified using the usual boundary layer theory approximations and then obtain
![]() (12)
(12)
In this study on Maxwell fluid flow, it is assumed that the normal stress is of the same order of magnitude as that of the shear stress in addition to the usual boundary layer approximation for deriving the component of the
momentum boundary layer Equation (12). This is properly accounted for by introducing ![]() into the
into the
momentum Equation (12); for details, see Motsa et al. [18] . In this present study, it is important to state that exponential heat source is adopted to account for internal distribution of temperature in energy equation. This con- cept can be traced to the idea of Crepeau and Clarksean [23] , Salem and El-Aziz [24] [25] , Animasaun et al. [26] and Animasaun [44] . The energy and concentration equations can be written as
![]() (13)
(13)
![]() (14)
(14)
Equations (8), (12), (13) and (14) are subject to the following boundary conditions
![]() (15)
(15)
![]() (16)
(16)
κ is the thermal conductivity, ![]() is the latent heat of the fluid and
is the latent heat of the fluid and ![]() is the heat capacity of the solid surface. In order to solve the problem completely in unbounded domains, it is possible to augment the boundary conditions by assuming certain asymptotic structures for the solutions at infinity. The formulation of the second term in Equation (15) states that the heat conducted to the melting surface is equal to the heat of melting plus the sensible heat required to raise the solid temperature
is the heat capacity of the solid surface. In order to solve the problem completely in unbounded domains, it is possible to augment the boundary conditions by assuming certain asymptotic structures for the solutions at infinity. The formulation of the second term in Equation (15) states that the heat conducted to the melting surface is equal to the heat of melting plus the sensible heat required to raise the solid temperature ![]() to its melting temperature
to its melting temperature ![]() (for details, see Epstein and Cho [45] ). The increase of temperature may also leads to a local increase in the transport phenomena by reducing the viscosity across the momentum boundary layer and so the heat transfer rate at the wall may also be affected greatly. Due to this, it is very important to account for the influence of temperature on the thermo- physical properties of UCM fluid as it flows over a melting surface within the boundary layer. However, it is known that physical properties of the fluid may change significantly when expose to significant internal generated heat energy across the space. For lubricating fluids, heat generated by the internal friction and the corresponding rise in temperature affect the viscosity of the fluid and so the fluid viscosity can no longer be assumed constant. In order to account for the variation in thermo-physical properties of the fluid as it flows past a horizontal melting surface, it is valid to consider the mathematical model of temperature dependent viscosity model used in Animasaun [35] and Sivagnana et al. [46] which was developed using the experimental data of Batchelor [34] together with the mathematical model of temperature dependent thermal conductivity model of [26] [35] as
(for details, see Epstein and Cho [45] ). The increase of temperature may also leads to a local increase in the transport phenomena by reducing the viscosity across the momentum boundary layer and so the heat transfer rate at the wall may also be affected greatly. Due to this, it is very important to account for the influence of temperature on the thermo- physical properties of UCM fluid as it flows over a melting surface within the boundary layer. However, it is known that physical properties of the fluid may change significantly when expose to significant internal generated heat energy across the space. For lubricating fluids, heat generated by the internal friction and the corresponding rise in temperature affect the viscosity of the fluid and so the fluid viscosity can no longer be assumed constant. In order to account for the variation in thermo-physical properties of the fluid as it flows past a horizontal melting surface, it is valid to consider the mathematical model of temperature dependent viscosity model used in Animasaun [35] and Sivagnana et al. [46] which was developed using the experimental data of Batchelor [34] together with the mathematical model of temperature dependent thermal conductivity model of [26] [35] as
![]() (17)
(17)
The classical models in Equation (17) are valid when![]() . These mathematical models together with classical similarity variables for temperature and concentration are modified to
. These mathematical models together with classical similarity variables for temperature and concentration are modified to
![]() (18)
(18)
It is worth mentioning that the first and fourth terms of Equation (18) are valid since![]() . Due to the relationship between dynamic viscosity, exponentially internal heat source and free stream temperature of UCM fluid as stated in the first term of Equation (18). Using Equation (19) and second term of Equation (18), it is easy to obtain
. Due to the relationship between dynamic viscosity, exponentially internal heat source and free stream temperature of UCM fluid as stated in the first term of Equation (18). Using Equation (19) and second term of Equation (18), it is easy to obtain
![]()
In this study, the idea of Vimala and Loganthan [47] and Animasaun [44] is followed to define thermal stratification![]() , solutal stratification
, solutal stratification ![]() at the melting wall
at the melting wall ![]() and at the free stream
and at the free stream ![]() are defined as
are defined as
![]() (19)
(19)
![]() (20)
(20)
From these models, it is valid to write the relation of the form
![]() (21)
(21)
![]() and
and ![]() are known as reference temperature and concentration respectively. It is worth noticing from Equation (21) that there exist two differences in temperature due to stratification which occur for all x at fixed pointy = 0 and the other that occurs for all x as
are known as reference temperature and concentration respectively. It is worth noticing from Equation (21) that there exist two differences in temperature due to stratification which occur for all x at fixed pointy = 0 and the other that occurs for all x as![]() . In view of this, it is valid to define temperature dependent viscous parameter ξ as first term in Equation (22). This assumption is based on the fact that (1) the stress tensor is a linear function of the strain rates as the fluid flows along a surface (2) the UCM fluid is isotropic. The ratio of the two terms in Equation (21) can thus produce the dimensionless thermal stratification parameter
. In view of this, it is valid to define temperature dependent viscous parameter ξ as first term in Equation (22). This assumption is based on the fact that (1) the stress tensor is a linear function of the strain rates as the fluid flows along a surface (2) the UCM fluid is isotropic. The ratio of the two terms in Equation (21) can thus produce the dimensionless thermal stratification parameter![]() . Likewise, the ratio of the two terms in Equation (20) can thus produce the dimensionless solutal stratification parameter
. Likewise, the ratio of the two terms in Equation (20) can thus produce the dimensionless solutal stratification parameter ![]()
![]() (22)
(22)
Upon using Equation (18) - Equation (22), we obtain
![]() (23)
(23)
![]() (24)
(24)
In order to write the governing equations and the boundary conditions in dimensionless form, the following non-dimensional quantities are introduced,
![]() (25)
(25)
It is important to note that the first two terms of Equation (25) automatically satisfy continuity Equation (8). Then, Equation (23) and Equation (24) becomes
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
The corresponding boundary conditions take the form
![]() (29)
(29)
![]() (30)
(30)
Here dimensionless viscoelastic parameter (Deborah number)![]() , temperature dependent thermal conductivity parameter
, temperature dependent thermal conductivity parameter![]() , Magnetic field parameter
, Magnetic field parameter![]() , Coefficient of thermal diffusivity
, Coefficient of thermal diffusivity![]() , Prandtl number
, Prandtl number![]() , Schmidt number
, Schmidt number ![]() Heat source parameter
Heat source parameter ![]()
and melting parameter![]() . The physical quantities of interest are the skin fric-
. The physical quantities of interest are the skin fric-
tion coefficient ![]() Local Nusselt number
Local Nusselt number ![]() and Local Sherwood number
and Local Sherwood number ![]() which are defined as
which are defined as
![]() (31)
(31)
where the wall skin friction![]() , heat transfer from the melting surface
, heat transfer from the melting surface ![]() and mass transfer from the melting surface
and mass transfer from the melting surface ![]() are defined following Abbas et al. [14] as
are defined following Abbas et al. [14] as
![]() (32)
(32)
Using Equation (25)
![]() (33)
(33)
the local Reynolds number is defined as ![]()
3. Method of Solution
Numerical solutions of the ordinary differential Equation (26) - Equation (28) with the Neumann boundary conditions Equation (29) and Equation (30) are obtained using classical Runge-Kutta method with shooting techniques. The BVP can not be solved on an infinite interval, and it would be impractical to solve it for even a very large finite interval. In this study, we impose the infinite boundary condition at a finite point![]() . The set of coupled nonlinear ordinary differential equations along with boundary conditions have been reduced to a system of seven simultaneous equations of first order for seven unknowns following the method of superposition Na [48] . In order to integrate the corresponding I.V.P. the values of
. The set of coupled nonlinear ordinary differential equations along with boundary conditions have been reduced to a system of seven simultaneous equations of first order for seven unknowns following the method of superposition Na [48] . In order to integrate the corresponding I.V.P. the values of![]() ,
, ![]() ,
, ![]() and
and ![]() are required, but no such values exist after the non-dimensionalization of the boundary conditions Equation (15) and Equation (16). It is important to report that, we may easily obtain
are required, but no such values exist after the non-dimensionalization of the boundary conditions Equation (15) and Equation (16). It is important to report that, we may easily obtain ![]() by setting
by setting![]() . The suitable guess values for
. The suitable guess values for![]() ,
, ![]() ,
, ![]() and
and ![]() are chosen and then integration is carried out. In this method of solution, Newton-Raphson method is embedded as root finding of the non-linear equations of the corresponding systems of seven first order ordinary differential equations. The seven initial conditions at
are chosen and then integration is carried out. In this method of solution, Newton-Raphson method is embedded as root finding of the non-linear equations of the corresponding systems of seven first order ordinary differential equations. The seven initial conditions at ![]() can now be defined as column vector with seven elements as
can now be defined as column vector with seven elements as
![]()
The calculated values for![]() ,
, ![]() and
and ![]() at
at ![]() are compared with the given boundary conditions in Equation(30) and the estimated values
are compared with the given boundary conditions in Equation(30) and the estimated values![]() ,
, ![]() ,
, ![]() and
and ![]() are adjusted to give a better approximation of the solution. Series of values for
are adjusted to give a better approximation of the solution. Series of values for![]() ,
, ![]() ,
, ![]() and
and ![]() are considered and applied with fourth-order classical Runge-Kutta method using step size
are considered and applied with fourth-order classical Runge-Kutta method using step size![]() . The above procedure is repeated until asymptotically converged results are obtained within a tolerance level of
. The above procedure is repeated until asymptotically converged results are obtained within a tolerance level of![]() . It is worth mentioning that there exist no related published articles that can be used to validate the accuracy of the numerical results. Equation (26) - Equation (30) can easily be solved using ODE solvers such as MATLAB’s bvp4c solver (see [49] ).
. It is worth mentioning that there exist no related published articles that can be used to validate the accuracy of the numerical results. Equation (26) - Equation (30) can easily be solved using ODE solvers such as MATLAB’s bvp4c solver (see [49] ).
Verification of the Results
In order to verify the accuracy of the present analysis, the results of Classical Runge-Kutta together with shooting (RK4SM) have been compared with that of bvp4c for the limiting cases when![]() ,
, ![]() ,
, ![]()
![]()
![]() and
and ![]() at various values of
at various values of ![]() and
and![]() . The comparison in the above cases is found to be in good agreement, as shown in Table 1. The good agreement is an encouragement for further study of the effects of other parameters on UCM fluid as it flows over a melting surface.
. The comparison in the above cases is found to be in good agreement, as shown in Table 1. The good agreement is an encouragement for further study of the effects of other parameters on UCM fluid as it flows over a melting surface.
4. Discussion of Results
The numerical computations have been carried out for various values of temperature dependent viscous parameter, thermal stratification parameter, solutal stratification parameter, Deborah number, magnetic field parameter, temperature dependent thermal conductivity parameter, Schmidt number, Prandtl number, space dependent heat source parameter, intensity of heat distribution on space parameter and melting parameter using numerical scheme discussed in the previous section. To avoid any corresponding effect(s) on the fluid flow (i.e. decrease in the volume and changing of state) of UCM due to high temperature when investigating the effect of dimensionless temperature dependent viscous and thermal conductivity parameters, variable “a1 = a2” in Equations (26) and (27) have been considered as unity. In order to illustrate the results graphically, the numerical values are plotted in Figures 2-14. Table 1 provides the numerical value of skin friction coefficients, reduced Nusselt numbers ![]() and Sherwood numbers
and Sherwood numbers ![]() for different values of Prandtl number and melting parameter. From Table 1, it is further seen that
for different values of Prandtl number and melting parameter. From Table 1, it is further seen that ![]() which is proportional to local heat transfer is small when
which is proportional to local heat transfer is small when ![]() and large when
and large when ![]() at a given value of Prandtl number. For instance, when
at a given value of Prandtl number. For instance, when![]() , the Nusselt number is estimated as
, the Nusselt number is estimated as ![]() while when
while when![]() , the Nusselt number is estimated as
, the Nusselt number is estimated as![]() . This result shows a significant increase in local heat transfer rate at the wall
. This result shows a significant increase in local heat transfer rate at the wall![]() . In real life, melting is a phase transformation process that is accompanied by absorption of thermal energy. Hence, this accounts for the absorption of thermal energy at the wall which corresponds to an increase in the rate of heat transfer with melting. This result is in good agreement with the report of Fukusako and Yamada [33] .
. In real life, melting is a phase transformation process that is accompanied by absorption of thermal energy. Hence, this accounts for the absorption of thermal energy at the wall which corresponds to an increase in the rate of heat transfer with melting. This result is in good agreement with the report of Fukusako and Yamada [33] .
Figure 2 and Figure 3 illustrate the influence of solutal stratification parameter on the concentration and
![]()
Figure 2. Concentration profiles ![]() for different values of solutal stratification parameter
for different values of solutal stratification parameter![]() .
.
![]()
Figure 3. Concentration gradient profiles ![]() for different values of solutal stratification parameter
for different values of solutal stratification parameter![]() .
.
![]()
Figure 4. Temperature profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 5. Temperature gradient profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 6. Velocity profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 7. Transverse velocity profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 8. Sheer stress profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 9. Concentration profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 10. Concentration gradient profiles ![]() for different values of thermal stratification parameter
for different values of thermal stratification parameter![]() .
.
![]()
Figure 11. Transverse velocity profiles ![]() for different values of temperature dependent viscous parameter
for different values of temperature dependent viscous parameter![]() .
.
![]()
Figure 12. Velocity profiles ![]() for different values of temperature dependent viscous parameter
for different values of temperature dependent viscous parameter![]() .
.
![]()
Figure 13. Temperature profiles ![]() for different values of temperature dependent thermal conductivity parameter
for different values of temperature dependent thermal conductivity parameter![]() .
.
concentration gradient profiles. The effect of ![]() is to decrease the concentration profiles of UCM fluid as it flows along horizontal melting surface. Physically, as magnitude of
is to decrease the concentration profiles of UCM fluid as it flows along horizontal melting surface. Physically, as magnitude of ![]() increases, this corresponds to a decrease of concentration at free stream (η = 4). Since diffusion of species is from region of higher concentration at free stream towards the region of lower concentration at the melting wall; hence, this account for decrease in
increases, this corresponds to a decrease of concentration at free stream (η = 4). Since diffusion of species is from region of higher concentration at free stream towards the region of lower concentration at the melting wall; hence, this account for decrease in![]() . It is well known fact in the study of heat and mass transfer that the behavior of concentration gradient
. It is well known fact in the study of heat and mass transfer that the behavior of concentration gradient ![]() which is proportional to local mass transfer rate is strong dependent on the nature concentration
which is proportional to local mass transfer rate is strong dependent on the nature concentration![]() . In view of this, an attempt is made to investigate the variations of concentration gradient profiles
. In view of this, an attempt is made to investigate the variations of concentration gradient profiles ![]() along similarity variable η with different values of solutal stratification parameter; for details see Figure 3. It is seen that concentration gradient is a decreasing function of
along similarity variable η with different values of solutal stratification parameter; for details see Figure 3. It is seen that concentration gradient is a decreasing function of![]() . It is observed that
. It is observed that ![]() decreases significantly at the melting surface. As expected,
decreases significantly at the melting surface. As expected, ![]() decreases significantly with increase in the magnitude of
decreases significantly with increase in the magnitude of ![]() near the wall while amount of concentration is very low near the melting surface. It is observed that increase in the magnitude of solutal stratification parameter has no significant effect on transverse velocity profile
near the wall while amount of concentration is very low near the melting surface. It is observed that increase in the magnitude of solutal stratification parameter has no significant effect on transverse velocity profile![]() , velocity profile
, velocity profile![]() , shear stress profile
, shear stress profile![]() , temperature profile
, temperature profile ![]() and temperature gradient profile
and temperature gradient profile![]() . Physically, solutal stratification parameter quantifies the ratio between concentration of UCM as it flows over horizontal melting surface to that of concentration at the free stream; this account for the reason why increase in the magnitude of
. Physically, solutal stratification parameter quantifies the ratio between concentration of UCM as it flows over horizontal melting surface to that of concentration at the free stream; this account for the reason why increase in the magnitude of ![]() on all the profiles mentioned above.
on all the profiles mentioned above.
The variations of temperature profiles ![]() along similarity variable η with different values of thermal stratification parameter are plotted in Figure 4. At a constant value of thermal stratification parameter, it is seen that
along similarity variable η with different values of thermal stratification parameter are plotted in Figure 4. At a constant value of thermal stratification parameter, it is seen that ![]() enlarges continuously as η grows. At all points in the fluid domain
enlarges continuously as η grows. At all points in the fluid domain![]() , it is seen that
, it is seen that ![]() decreases with an increase in the magnitude of stratification parameter with a negligible decrease few distance from the melting surface and significant decrease thereafter till free stream. Physically, increase in the magnitude of thermal stratification parameter corresponds to a systematic way of decreasing the heat energy from the free stream (i.e. to control the heat energy from hot environment in the layer above into the fluid domain). It is worth mentioning that as the heat energy is reducing, hence the temperature of the UCM fluid within the fluid layer is decreasing. The negligible decrease near the melting surface shown in Figure 4 can be traced to the rate of melting which occurs at the wall (i.e.
decreases with an increase in the magnitude of stratification parameter with a negligible decrease few distance from the melting surface and significant decrease thereafter till free stream. Physically, increase in the magnitude of thermal stratification parameter corresponds to a systematic way of decreasing the heat energy from the free stream (i.e. to control the heat energy from hot environment in the layer above into the fluid domain). It is worth mentioning that as the heat energy is reducing, hence the temperature of the UCM fluid within the fluid layer is decreasing. The negligible decrease near the melting surface shown in Figure 4 can be traced to the rate of melting which occurs at the wall (i.e.![]() ). The result is in good agreement with the fact that a decrease in temperature is significant near free stream and negligibly as η tends from 4 to 0. It is also noticed that this decrease obey the melting boundary condition of temperature at the wall
). The result is in good agreement with the fact that a decrease in temperature is significant near free stream and negligibly as η tends from 4 to 0. It is also noticed that this decrease obey the melting boundary condition of temperature at the wall![]() . It is observed in Figure 5 that temperature gradient is a decreasing function of thermal stratification at all point of η. From this graph, it is evidently to report that
. It is observed in Figure 5 that temperature gradient is a decreasing function of thermal stratification at all point of η. From this graph, it is evidently to report that ![]() which is proportional to local heat transfer rate increases significantly with an increase in stratification. In Figure 5, it is noticed that
which is proportional to local heat transfer rate increases significantly with an increase in stratification. In Figure 5, it is noticed that ![]() increases negligible at the free stream with an increase in St.
increases negligible at the free stream with an increase in St.
In this study, setting m = 0 can seriously affect the melting processes at the wall. In addition to this fact, existence of melting at the wall together with an increase in thermal stratification parameter depicts anegligible increase in longitudinal velocity and significant increase in transverse velocity (see Figure 6 and Figure 7). As temperature decreases due to an increase in thermal stratification parameter, velocity profile is expected to decrease as reported in [44] . It is worth noticing that such effect exists due to the presence of suction and the kind of fluid under consideration (Casson fluid). In this research, mathematical model which denotemelting heat transfer has replaced the suction at the wall. It is worth noticing that the result we obtained here is in good agreement with that of Figure 6 reported in [32] .
We believe that this influence requires further investigation by replacing melting heat transfer model with suction model (i.e. to study the effect of suction on UCM fluid with variable thermo-physical properties subject to thermal and solutal stratification). It is also important to report that the influence of free stream temperature together with internal exponential heat source account for the increase in velocity and transverse velocity of UCM as it flows. In fact, these influences totally subdues the effect of increasing stratification which ought to decrease velocity profiles as reported in [44] . Figure 8 shows that the shear stress profile increases near the melting surface with an increase in thermal stratification parameter. Opposite effect is observed near free stream (η = 4). Figure 9 and Figure 10 illustrate the effect of thermal stratification parameter on the concentration of UCM fluid flow over melting surface towards thermal stratified environment. It is seen that the concentration increases negligibly with![]() ; see Figure 9 for details. It is also observed that concentration gradient is a decreasing function of
; see Figure 9 for details. It is also observed that concentration gradient is a decreasing function of ![]() near the free stream. The variations of
near the free stream. The variations of ![]() along η with different values of ξ are plotted in Figure 11. It is seen that the increase of ξ leads to the enhancement of the velocity profiles. We further notice that, increase in the magnitude of ξ has no effect on
along η with different values of ξ are plotted in Figure 11. It is seen that the increase of ξ leads to the enhancement of the velocity profiles. We further notice that, increase in the magnitude of ξ has no effect on ![]() near the melting wall. As shown in Figure 11, ξ has an evident effect on
near the melting wall. As shown in Figure 11, ξ has an evident effect on ![]() that the larger the value of ξ is, the greater the velocity is. The physics behind this is that, as magnitude of ξ increases at a constant value of
that the larger the value of ξ is, the greater the velocity is. The physics behind this is that, as magnitude of ξ increases at a constant value of![]() , this corresponds to an increase in temperature difference of
, this corresponds to an increase in temperature difference of![]() .
.
Hence, this increase in temperature weakens the intermolecular forces which hold the molecule of UCM so tight. In view of this, the dynamic viscosity is gradually reduced and corresponds to increase in velocity as shown in Figure 11 and Figure 12. It is further observed in Figure 12 that increases in the magnitude of temperature dependent viscous parameter has negligible effect on velocity profiles near the free stream. Physically, the temperature of UCM near the hot environment (upper layers at the free stream) is almost the same. In such a situation, the flow velocity approaches to the maximum value. In this study, it is important to note that increase in the temperature dependent thermal conductivity parameter (ε) at a constant value of δ corresponds to an increase in temperature difference![]() . This explains the increase in temperature profiles shown in Figure 13 due to increase in the magnitude of ε. Figure 14 illustrates the effects of solutal stratification and Schmidt number on Sherwood number
. This explains the increase in temperature profiles shown in Figure 13 due to increase in the magnitude of ε. Figure 14 illustrates the effects of solutal stratification and Schmidt number on Sherwood number ![]() which is proportional to local mass transfer rate. At a constant value of Schmidt number, the Sherwood number of the UCM fluid flow increases significantly with an increase in Solutal stratification parameter. In addition, it is observed that
which is proportional to local mass transfer rate. At a constant value of Schmidt number, the Sherwood number of the UCM fluid flow increases significantly with an increase in Solutal stratification parameter. In addition, it is observed that ![]() increases with an increase in the magnitude of Schmidt number at a constant value of
increases with an increase in the magnitude of Schmidt number at a constant value of![]() . Due to the nature of temperature and concentration of the present study at melting surface which is lesser than that of free stream, it is of important to also investigate the effects of solutal stratification and Schmidt number on concentration gradient
. Due to the nature of temperature and concentration of the present study at melting surface which is lesser than that of free stream, it is of important to also investigate the effects of solutal stratification and Schmidt number on concentration gradient ![]() at a point near hot environment (η = 4). It is worth noticing that previous analysis has resolved the initial value problem of the B.V.P. by producing all the missing values at
at a point near hot environment (η = 4). It is worth noticing that previous analysis has resolved the initial value problem of the B.V.P. by producing all the missing values at![]() . Table 2 displays the effect of increasing the magnitude of
. Table 2 displays the effect of increasing the magnitude of ![]() over concentration gradient
over concentration gradient![]() . It is observed that at a constant value of
. It is observed that at a constant value of![]() , local mass transfer at the free stream (η = 4) increases significantly with
, local mass transfer at the free stream (η = 4) increases significantly with![]() . From Table 2, it is observed that at a constant value of
. From Table 2, it is observed that at a constant value of![]() , the local mass transfer rate decreases with
, the local mass transfer rate decreases with![]() .
.
5. Conclusion
Similarity solutions of steady UCM fluid flow over a melting surface; considering a case in which the flow is subjected to thermal and solutal stratification have been studied theoretically. The corresponding influence of thermal stratification, solutal stratification, variation in viscosity and thermal conductivity due to temperature is properly considered. The governing (dimensional) partial differential equations are converted into (dimensionless) nonlinear ordinary differential equations by using similarity transformation before being solved numerically using fourth order Runge-Kutta integration scheme along with shooting techniques. Results for the skin friction coefficient, local Nusselt number, local Sherwood number, transverse velocity profiles, velocity profiles, temperature profiles as well as concentration profiles are presented for different values of the pertinent parameters. Effects of Prandtl number, the melting parameter, temperature dependent viscous parameter, temperature dependent thermal conductivity parameter, solutal and thermal stratification on the flow and heat transfer characteristics are thoroughly examined. For accurate and correct analysis of fluid flow in which (![]() or
or![]() )
) ![]() the mathematical models of temperature dependent viscosity and thermal conductivity must be modified as explained in this article. In addition, if fluid flow along vertical surface with constant viscosity and thermal
the mathematical models of temperature dependent viscosity and thermal conductivity must be modified as explained in this article. In addition, if fluid flow along vertical surface with constant viscosity and thermal
conductivity is to be investigated; the term ![]() or
or ![]() in the Boussinesq approximation must also be modified. The concentration
in the Boussinesq approximation must also be modified. The concentration ![]() and concentration gradient
and concentration gradient ![]() of upper convected Maxwell fluid flow over a melting surface are decreasing functions of the solutal stratification parameter. The Sherwood number
of upper convected Maxwell fluid flow over a melting surface are decreasing functions of the solutal stratification parameter. The Sherwood number ![]() decreases significantly at the melting surface with
decreases significantly at the melting surface with![]() . At a constant value of Schmidt number, Sherwood number is an increasing function of solutal stratification parameter. Longitudinal velocity and transverse velocity are increasing functions of thermal stratification parameter. The classical effect of the magnitude of stratification on velocity is subdued by the intense free stream temperature together with internal exponential heat source. The temperature of UCM fluid flow over a melting surface is an increasing function of variable thermal conductivity parameter.
. At a constant value of Schmidt number, Sherwood number is an increasing function of solutal stratification parameter. Longitudinal velocity and transverse velocity are increasing functions of thermal stratification parameter. The classical effect of the magnitude of stratification on velocity is subdued by the intense free stream temperature together with internal exponential heat source. The temperature of UCM fluid flow over a melting surface is an increasing function of variable thermal conductivity parameter.
Acknowledgements
The authors wish to express their thanks to the anonymous Reviewer for his/her valuable and interesting comments.