Impact of the Waves on the Sea Surface Roughness Length under Idealized Like-Hurricane Wind Conditions (Part II) ()
1. Introduction
Ocean surface gravity waves are one manifestation of the interaction between the atmosphere and the ocean, which can have a significant impact on the transfer of momentum and enthalpy (heat) across the atmosphere- ocean interface [1] . Conventionally, the bulk parameterization is commonly used in most atmospheric and ocean models, where it is assumed that surface stress (τ) is only function of the wind velocity, without any dependence on the sea state. Following [2] , the roughness length (z0) is expressed in terms of the friction velocity (u*), acceleration due to gravity (g), and a constant (zch), which is representative of an equilibrium sea. The parameter zch was based on measures from moderate to weak wind regimes (winds below 25 m/s). However, both observation and numerical modeling studies have indicated that the surface stress is also related to the sea state, in other words, it is dependent of the wind wave spectrum.
The presence of the waves cause significant changes in surface stress that influences directly or indirectly the planetary boundary layer over the oceans [3] [4] . Moreover, the waves expressively reduce the intensity of the mesoscale extratropical systems near the surface [5] - [7] , improve wave forecasting during midlatitude cyclogenesis [8] , and modulate storm track regions. From simulations with an atmospheric-ocean wave coupled model, [9] showed that waves influence high frequency variability of the storm tracks in South and North Hemispheres. In addition, the impact of the waves is more significant for North Hemisphere in coupled experiments.
[6] analyzed the evolution of an idealized low pressure system with a coupled atmospheric-ocean wave model. They observed that in the storm area, during a fast-growing cyclone, because of the intense and variable wind, the prevalent effects of the two-way coupling are to increase the surface roughness, to enhance the friction velocity, and to reduce the surface wind speed U10 and sea wave high (SWH). The authors pointed out that the increased friction in the region of intense air-sea interaction is the dominant feature of the two-way coupling that consequently produces a storm with diminished strength.
To evaluate the effect of surface waves on air-sea momentum flux over mature and growing seas [10] combined the WW3 ocean wave prediction model, the equilibrium spectrum model [11] , and a wave boundary layer model (WBL). In this study WW3 model was used to estimate the wave spectra, while the equilibrium spectrum model was used to estimate the spectra in the high-frequency range, where the full spectra was introduced to the wave boundary layer model [12] to compute the drag coefficient (CD) and u*. In cases of mature sea, their results showed that the Charnock coefficient is estimated to be about 0.01 - 0.02 and the drag coefficient increases as wind speed increases. With growing seas, for uniform winds less than 30 m/s, the drag coefficient is larger for younger seas, which agrees with previous theoretical and observational studies. However, for wind speed higher than 30 m/s their results show a different trend: very young waves yield less drag and drag increases as waves become older.
[13] focused on investigation of the effect of surface waves on air-sea momentum exchange in extreme complex sea forced by idealized tropical cyclones. The authors showed that CD strongly depends on the wave field. Moreover, hurricane intensity and translation speed are major factors that determine the spatial distribution of CD. At strong winds above 30 m/s, the combined models predict significant reduction of CD as the wind speed enhance.
[14] (hereafter termed Part I) investigated the impact of the waves, for mature and growing seas, on sea surface roughness length. Various numerical experiments were performed for constant winds from 15 to 45 m/s with the WW3 model in a basin domain of 3000 km, in north-south direction, and 1500 km in east-west extent. The WW3 ocean wave model determined the full wave spectrum while a simple algorithm computed CD, u*, z0, and U10 in cases of Charnock and Smith relations (see Part I).
The main results of Part I showed that when the ocean is characterized by young waves, both z0 and CD increases while U10 decreases. For old waves CD, z0, and U10 behave as in Charnock relation. Further, in cases of winds higher than 25 m/s CD was higher to young waves than to old waves. For winds bellow 25 m/s there is a week tendency to a reduction of CD for young waves. In the present study it is investigated the impact of the waves on the sea surface roughness length under hurricane wind conditions. Thus WW3 numerical model is combined in a one-way mode with a simple algorithm (Part I) to estimate CD, u*, z0, and U10 under idealized hurricane wind conditions. A brief outline of the WW3, simplified algorithm, experimental design, and method used to investigate the impact of waves on sea surface roughness length under extreme wind conditions is introduced in Section 2. Section 3 describes results of the experiments with translation speed and intensity of the hurricane. The summary and conclusions are given in Section 4.
2. Methodology
Results from theoretical and numerical modeling studies have shown that z0 (CD or u*) is a function of a single parameter called wave age defined as cp/u*, where cp is the phase speed of the spectral peak frequency and u* is the friction velocity. The wave age indicates the stage of wave development because the phase speed cp increases progressively during wave growth [15] [16] . This parameter is a good measure of the sea state since it distinguishes the steeper and young waves (β < 10) from the older and smother waves (β > 10).
Experimental Design
To evaluate the impact of the waves on the sea surface roughness length it is used the WW3 numerical model joined with a very simple algorithm, which estimates CD, u*, z0, and U10, in one-way mode (not coupled). More detail about the WW3 and the simplified algorithm is given in Part I. The algorithm computes the surface parameters in two ways; in the first, no dependence with sea state is considered and the Charnock constant is used (zch = 0.0185). In the second, sea surface roughness length is dependent on the sea state and wave age takes the place of Charnock constant.
Momentum, heat, and moisture fluxes in the atmospheric boundary layer over the oceans are directly related to CD. In the conventional theory of the boundary layer CD is connected with surface roughness length, which is typically defined by Charnock relationship [2] in terms of u* and g,
 (1)
(1)
Following [17] , over the sea β (Charnock parameter) has a constant value of 0.0185. However, recent researches have been shown that β is not constant and must be related with the sea state. The relationship between z0 and the sea state can be expressed by two distinct forms: in terms of wave age dependence [16] or in terms of wave-induced-stress, according to [18] . By this reason, Equation (1) is reformulated and results in,
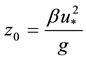 (2)
(2)
where 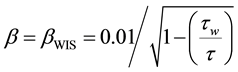 or
or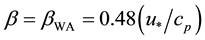 . The subscripts “WA” and “WIS” refers, respectively, to wave age (parameter based on [16] ) and wave-induced-stress (parameter based on [4] ) formulations. The terms τ and τw denote, respectively, total stress and stress due to the presence of the waves. Results from [7] showed that both parameters (WA or WIS) produced similar results for real storm conditions. In the present study, due to implementation simplicity, [16] theory is applied.
. The subscripts “WA” and “WIS” refers, respectively, to wave age (parameter based on [16] ) and wave-induced-stress (parameter based on [4] ) formulations. The terms τ and τw denote, respectively, total stress and stress due to the presence of the waves. Results from [7] showed that both parameters (WA or WIS) produced similar results for real storm conditions. In the present study, due to implementation simplicity, [16] theory is applied.
At the frequency peak (fp), cp is computed according to the dispersion relation of the gravity wave,
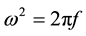 (3)
(3)
 (4)
(4)
where ω is the angular frequency and K is the wave number.
To evaluate the effect of hurricane translation speed (HTS) and its intensity, numerical simulations with WW3 model were designed (Table 1). Thus, following the idea of [13] , three idealized hurricanes with different translation speeds (0, 5, and 10 m/s) and maximum wind speed (MWS) at the centre of the hurricane (35, 45 e 55 m/s) were performed to force the wave model. Each idealized hurricane presents maximum speed at the centre, diminishing symmetric and concentrically from the centre to the periphery (Figure 1). The hurricane also moves to north with different translation speed.
The WW3 model runs for 72 hours from the rest (sea without waves) with time step and input wind speed of 1800 s, 24 directions (directional resolution), spatial resolution of 0.2˚ × 0.2˚, and 4000 meters depth. It extends 3000 km in the south-north direction and 1500 km in the east-west extent. The model grid is spatially regular on latitude-longitude grid.
In the following discussion, the results of all numerical experiments are presented after a spinup time of 56 hours, when a quasi steady state is achieved.
![]()
Figure 1. Wind fields for the Idealized experiment with hurricanes, which are moving with different HTSs (0, 5 and 10 m/s).
3. Results and Discussions
3.1. Effect of Hurricane Translation Speed
Spatial distribution of SWH for different HTS produced by idealized experiments is shown in Figures 2(a)-(c). It can be seen that as the HTS increases, SWH in the front-right quadrant of the storm track become higher and longer, while those in the opposite quadrant become lower and shorter. [10] and [13] showed that for a fast-moving hurricane, the dominant waves in the front-right quadrant are mostly determined by resonance effect when the group velocity is close to the HTS. The maximum values of SWH and mean wave length in the fast-moving hurricane reach up to 12 and 343 meters, respectively, against 8 and 176 meters in the stationary hurricane case, HTS of 0 m/s.
Distributions of the input wave age representing the state of the growth of wind waves relative to local wind forcing are presented in Figure 2(d) and Figure 2(f). In the front-right quadrant of the hurricane’s track waves become older, while those in the rear-left quadrant become younger. According to [13] waves in the front-right quadrant are exposed to prolonged forcing from wind (resonance). Thus, resonance produces higher, longer, and older waves in the front-right region. On the other hand, waves to the rear-left quadrant experience limited fetch and duration of wind forcing and waves become lower, shorter, and younger as the HTS increases.
Figures 2(g)-(i) show that as HTS increases waves become lower, shorter, younger and rougher (high values of z0) in the rear-left quadrant, whereas in the front-right quadrant z0 decreases. These results agree with observational and modeling studies, which show a strong inverse dependence between z0 and wave age. This means that, young waves produce rougher surface then older waves. The results show that the effect of waves on z0 values is more pronounced during developing sea. However, [10] showed that for very young waves during strong wind conditions (>30 m/s) there is a slightly tendency for decreasing in z0, instead.
![]()
Figure 2. Spatial distributions of significant wave height (a)-(c); wave age (d)-(f); sea surface roughness (g)-(i); drag coefficient (j)-(l); and wind velocity at 10 meters (m)-(o); All figures are produced by idealized hurricanes (MWS = 45 m/s) with a HTS of (left) 0, (centre) 5, and (right) 10 m/s. The dark circle represents the RMV in the centre of the storm.
For stationary idealized tropical storm the values of CD (Figures 2(j)-(l)) decrease symmetric and concentrically from the centre of the hurricane to its periphery. As the HTS increases, CD also increases in the rear-left quadrant where waves are shorter, younger, and rougher. In this case, the spatial pattern suffers substantial modifications becoming more asymmetric. In the front-right quadrant, where waves are higher, longer, and older, CD becomes lower than in the opposite quadrant. This asymmetric spatial pattern of CD causes a no uniform hurricane wind velocity distribution (Figures 2(m)-(o)). It can be seen that wind speed (U10) suffers a significantly reduction where waves are younger and rougher, while in the front-right quadrant, where waves are higher, longer, and older, U10 experiences just slightly changes.
Table 2 shows surface variables extracted from two different points around the region of maximum speed. Those points are located in the rear-left and front-right quadrants of the maximum wind velocity at the centre of the hurricane (black circles in Figures 2(a)-(o)). From this table, it can be seen that as the HTS increases more expressive difference rises between rear-left and front-right quadrants. For example, in cases of HTS of 10 m/s and maximum wind speed at the centre equal to 35 m/s the SWH produced is of the order of 7.8 m, in the rear-left, against 13.1 m in the front-right quadrant, a difference of 5.3 m. In the case of stationary hurricane the difference between the opposite quadrants is approximately 0.5 m, a value of 91% less than the fastest hurricane. The reason to this pronounced difference in SWH is due the fact that in the front-right quadrant the relative velocity is greater than in the opposite quadrant, once the hurricane move northward.
As the phase velocity of the waves become similar or near the HTS, winds act on surfaces with higher waves, unlike in the opposite quadrant. Other variables are sensible to those wind velocity differences, as for instance; wave age, z0, CD, U10 and u*. Differences in those values cause spatial asymmetries in the structure of the atmospheric system at the surface, see Figures 2(a)-(o). As can be seen, from Figures 2(g)-(l), z0 and CD suffers expressively modifications in its spatial pattern due to the asymmetry of the SWH. Higher values of those two quantities must cause a decrease in the moisture and mass convergence via diminishing the magnitude of the wind. The decrease in the magnitude of the wind, near surface, substantially, modifies the entire structure of the storm at surface [6] . Table 2 also shows that as the intensity and translation speed of the hurricane increase larger differences rises in the surface variable values. For instance, a HTS with 10 m/s with maximum wind velocity at the centre of 55 (45) m/s supports SWH in the order of 17.4 (11.9) m, in the rear-left quadrant and 33.5 (23) m in the front-right quadrant. The anti-symmetric behavior of the waves causes substantial changes in some surface parameters like z0 and U10.
3.2. Effect of Hurricane Intensity
Figure 3 shows the scatterplot of CD and z0 as function of the wave ages, as estimated from the idealized tropical storm experiments with different translation speeds and centre of maximum velocity, for all grid points. The results are color coded according to HTS at each grid point. For CD (Figures 3(a)-(c)) the figure clearly shows that most of the increased CD values are found in young waves (wave age less than 15) with maximum velocity at the centre of 55 m/s. In wave ages ranging from 15 to 35 the decrease of CD with the increase of the wave age is less pronounced. In fact, for wave ages higher than 35, the values of CD present a different trend, i.e. for wave age higher than 35 the values of CD become slightly constant. This means that, in cases of young waves the sea acts more vigorously on CD (and on z0) than do old waves. This pattern can be more accentuated in cases of most intense storms, as observed in Figures 3(a)-(c). In fact, in cases of young waves, as the intensity of the hurricane increases CD also increases. For example, we have a no dimensional value of CD equal to 9 × 10−3 (6.8 × 10−3) for wave age value of 5, in the case of MWS of 55 (35) m/s (Figure 3(b)). This mean CD is larger for young sea (wave age less than 15) than for old sea (wave age higher than 15). However, [13] show different results. According to authors, in cases of very young waves for moving hurricanes CD decreases. Similar and interesting results are found in the case of z0 versus wave age (Figures 3(d)-(f)). Until the wave age threshold limit of 15, sea surface roughness length decreases as the waves become older. Above the threshold of 15 (old waves) it seems that the waves do not affect z0, once its values hold constant with wave age. This result resembles to the behavior of the constant Charnock parameter (Part I).
In Figure 4, zch is plotted against wave ages at all grid points as in Figure 3, with different colors assigned according to the relative WW3 simulation. In this figure zch, for different MWS at the hurricane centre, is set in perspective with wave ages. Interesting aspects can be observed. Its well know that zch in the bulk parameterization is equal to 0.0185, which is used in most atmospheric numerical models. However, for MWS at the hurricane centre of 35 m/s (Figure 4(a)) it is seen that zch undergoes modifications for different wave stages. In fact, young waves produce higher values of zch while old waves is related to lower values of zch. Moreover, it can be
![]()
Figure 3. Scatter plots of the CD (a-c) and z0 (d-f) as a function of wave ages in all grid points for storms with translation speeds of 0, 5 and 10 m/s and different centre of maximum velocity 35 (black points), 45 (red points) and 55 m/s (blue points).
![]()
Figure 4. Scatter plots of the zch as a function of wave ages in all grid points for storms with different centre of maximum velocity 35 (a), 45 (b) and 55 m/s (c) and translation speeds of 0 (black points), 5 (red points) and 10 m/s (blue points).
![]()
Table 2. Surface variables for experiments with different hurricane translation speed (0, 5 and 10 m/s), and different intensities at the centre of the system (35, 45 and 55 m/s).Values in the left where extract from rear-left quadrant, while values in the right part represent front-right quadrant.
also seen that different HTS produce different behavior of zch. As can be seen from Figure 4(b), most of the points produced by different HTS are related to high values of zch than proposed by [2] , especially for young waves. In the case of the strong hurricane (Figure 4(c)), the majority of the points for young and old waves lie above the Charnock threshold of 0.0185. In addition, the rate of increased values of zch with the wave ages is higher as the intensity of the hurricane increases.
4. Conclusions
The effect of the surface waves over sea surface roughness length (z0) and drag coefficient is investigated by combining an ocean wave model and a simplified algorithm. The combined model estimates z0, CD, U10 and u*. Computations were done for two distinct conditions: in the first, the Charnock constant (zch) was applied to the algorithm, while in the second condition zch is computed from the wave age to include the effect from the sea. This investigation was possible through numerical simulations with the WW3 model for complex wind conditions. The numerical experiments were performed for idealized hurricanes with different translation speed (0, 5 and 10 m/s) and maximum wind speed at the centre (35, 45 and 55 m/s).
It can be observed that as the HTS increases SWH, in the front-right quadrant of the storm track become higher, longer and older (more developed waves), while those in the opposite quadrant become lower, shorter and younger (in the state of wave development). As the hurricane translations speed increases, lower, shorter and younger waves in the rear-left quadrant produce higher sea drag and sea surface roughness; higher, longer and old waves produce less drag and lower values of sea surface roughness. This results, which are in agreement with modeling and observational studies, suggest that sea drag and sea surface roughness are strongly related to the state of developing sea, or wave development. As the hurricane translation speed increases, from a stationary to a fast-moving condition, it causes more asymmetry in the spatial pattern of drag coefficient accentuating the discrepancy between values in the right-front and rear-left quadrants.
Other important result is that the wind velocity at 10 meters is strongly reduced in the rear-left quadrant where the waves cause more drag. More reduced wind speed is observed in the cases of fast hurricanes (Exps B and C). The reduction in the wind intensity is because younger waves induce more roughness and higher sea drag values. This reduction is strongly dependent on the HTS and the intensity of the hurricane. As for example, for the same HTS young waves will produce more drag (or z0) in cases where the maximum wind velocity at the hurricane centre is higher. The results also show that this dependence between wave age and sea drag is less pronounced as the waves become older.
It was observed that zch must change for different wave stages. Young waves produce higher values of zch, while old waves are related to lower values of zch. However, the increase or decrease of zch depends on the HTS, where young waves in stationary hurricane (0 m/s) cause higher values of zch than young waves in moving hurricanes (5 and 10 m/s). In addition, there is just a slight increase in zch as the hurricane intensity increases. In all experiments, young waves overestimate zch values, when compared with the Charnock constant. In spite of old waves be related to underestimated values of zch, there is no a clear relationship between older waves and the Charnock constant.
These conclusions support the idea to use more complex model combined to the WW3 issuing the effects of the waves on the planetary boundary layer structure. One manner to do that is to use a simple planetary boundary layer model with a wave model. This kind of studies can bring more insight into the physical processes, which occur over ocean with different sea state conditions. An additional possibility is to couple atmospheric and ocean wave models to evaluate the feedback between waves and storm development, which has been done since the last two decades. We emphasize that despite idealized experiments are powerful tools to understand physical processes of isolated systems, more realistic experiments efforts including real data must be held, which is the authors future intention. Although modeling studies performed here do not use a more sophisticated model to estimate surface variables (CD, z0, U10 and u*), they present similar results as compared with coupled experiments.