1. Introduction
Compared to conventional access methods, Time Division Multiple Access (TDMA) and Frequency Division Multiple Access (FDMA), the CDMA has three mainly advantages: it is a multiplexing scheme based on pseudo-random codes, a spread spectrum system with a wide frequency band, and it occurs security of the air interface. Currently one finds its applications in cellular telephony and satellite geolocation systems, GPS and Galileo. The DSSS method is the technique that is adopted by CDMA mobile networks. To implement it, one needs to find primitive polynomials enabling to characterize LFSR [1] .
In this work we present firstly the polynomials that are used for the CDMA and their corresponding Maximum Length Sequences (MLS). Then, we give their block diagrams and implement them in Scialab/Xcos. Thereafter, we model the Pseudo Noise Generator I-Channel (PN-I) and Q-Channel (PN-Q). Moreover, the Q-Channel is designed and we give a simulation and analysis of direct sequence spreading in Xcos using this channel. Lastly to show the wide range of possibility given by our simulation method, we model another kind of Sequence Generator, the Gold Code used for GPS, and make detail analysis of generated sequences.
2. Use of MLS for CDMA
For CDMA (IS-95 and CDMA-2000), there are mainly three polynomials used in the spreading process. The first two are of degree 15 and are contained in Quadrature Phase Shift Keying (QPSK) modulation.
 (1)
(1)
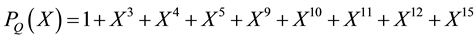 (2)
(2)
CDMA also uses another register i.e. the “Long Code Generator”, it is a LFSR modelled by a polynomial of degree 42, it intervenes in the allocation of user codes (Multiple Access) [2] [3] .
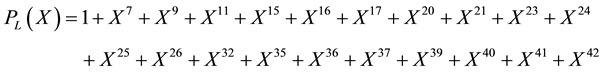 (3)
(3)
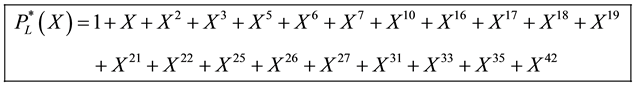 (4)
(4)
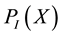 is a primitive polynomial, it serves to characterize and to build LFSR circuits; in its expression each monomial
is a primitive polynomial, it serves to characterize and to build LFSR circuits; in its expression each monomial 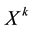 permit to know the feedback taps. Two main configuration of LFSR exists, the Simple Shift Register (SSRG) or Fibonacci LFSR; and Modular Shift Register (MSRG) or Galois LFSR.
permit to know the feedback taps. Two main configuration of LFSR exists, the Simple Shift Register (SSRG) or Fibonacci LFSR; and Modular Shift Register (MSRG) or Galois LFSR. 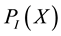 help to construct SSRG, to make a MSRG based on
help to construct SSRG, to make a MSRG based on 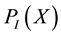 we determine the reciprocal polynomial or connection
we determine the reciprocal polynomial or connection
polynomial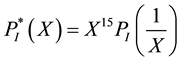 .
. 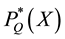 and
and 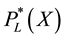 follow the same process of construction. The output
follow the same process of construction. The output
sequences given by these LFSR are called m-sequence or MLS because of their period equal to 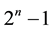 with
with 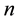 the degree of the characteristic polynomial [4] . The Direct Sequence Spread Spectrum is a CDMA method using MLS to provide a multiple access, scrambling information, and spread the signal frequency spectrum. This gives a flexible allocation of radio resources and an efficient utilization of frequency band.
the degree of the characteristic polynomial [4] . The Direct Sequence Spread Spectrum is a CDMA method using MLS to provide a multiple access, scrambling information, and spread the signal frequency spectrum. This gives a flexible allocation of radio resources and an efficient utilization of frequency band.
3. Advanced Method for LFSR Analysis under Scilab/Xcos
To make a detailed study of the LFSR and in particular those of CDMA, we use Scilab an open source software for numerical computation [5] to analyze pseudo-noise sequences. With Xcos, one of its tools, we set up a process for the establishment of LFSR.
3.1. Modeling PN-I Generator with Mask
Figure 1 is the MSRG for the I-channel that corresponds to the polynomial given by equation (1). A mask was added to obtain the same sequence but shifted in time [6] ; this allows to assign several codes for the DSSS, each with a particular shift.
This register is modelled with Xcos as shown in Figure 2.
![]()
Figure 2. I-Channel MSRG with mask under Xcos.
Legend
The used blocks in the model are described below:
 : This is the main component of this model. It has been configured to only store one bit (double). Also another reason why it is used here is the ability to set the initial condition 1 or 0.
: This is the main component of this model. It has been configured to only store one bit (double). Also another reason why it is used here is the ability to set the initial condition 1 or 0.
![]() : Connected to each block, it serves as synchronization. This is the block trigger successive feedback. Each activation state, one chip is obtained.
: Connected to each block, it serves as synchronization. This is the block trigger successive feedback. Each activation state, one chip is obtained.
![]() : This item is used to record the outputs of the LFSR. It is a buffer that is configured to record a predetermined number of data. When full, the data is replaced with the new.
: This item is used to record the outputs of the LFSR. It is a buffer that is configured to record a predetermined number of data. When full, the data is replaced with the new.
: To control the simulation time, this block is required. In this case, it synchronizes with the blocks To workspace and Clock.
3.2. Modeling PN-Q Generator with Mask
In the same way, the MSRG register for the Q-Channel can be design. Its block diagram in Figure 3 is implemented in Scilab/Xcos and represented in Figure 4.
The behaviour of the designed PN generator has to be checked with respect to the correlation.
4. Correlation of Generated Sequences
Here, we consider the MSRG for the Q-channel. Then we determine a sequence without the mask (MLS15). Thus, we generate its Auto Correlation Function ![]()
![]() . We also consider the same signal with the mask (MLS15m). The cross correlation function of the two signal is
. We also consider the same signal with the mask (MLS15m). The cross correlation function of the two signal is![]() . The correlation functions are plotted in Figure 6.
. The correlation functions are plotted in Figure 6.
Figure 6 gives the spectrum of the correlation. The spectrum of the autocorrelation function shows an interesting noise behaviour of the signal coming from the PN generator. The spectrum of the cross correlation function shows the effect of the mask that delays the pseudo noise.
Interpretation and Theoretical Verification of Results
Figure 5 shows first output sequences from the block To workspace (MLS15) without mask; and output from
block To workspace (MLS15m) with mask. The initial loading of the LFSR is ![]() that corresponds to the
that corresponds to the
long division![]() . The mask shift the initial sequence to
. The mask shift the initial sequence to ![]() positions; for our case, the sequence of the
positions; for our case, the sequence of the
mask is ![]() and we denote by
and we denote by ![]() the polynomial that correspond to the mask.
the polynomial that correspond to the mask.
![]()
Figure 4. Q-channel MSRG with mask under Xcos.
![]()
Figure 5. Firts output sequences given by the modelization.
![]()
Figure 6. Correlation of MLS sequences using scilab.
![]() (5)
(5)
We want to find ![]() such that:
such that:
![]() (6)
(6)
By calculation we get ![]() and the relative delay between MLS15 and MLS15m is given by
and the relative delay between MLS15 and MLS15m is given by ![]() [2] . It can be clearly seen in the graph of
[2] . It can be clearly seen in the graph of ![]() that the maximum is obtained at this position of
that the maximum is obtained at this position of![]() . This demonstrates the effectiveness of this method to get quickly the exact shift position of the pseudo-noise sequence by using Scilab and Xcos.
. This demonstrates the effectiveness of this method to get quickly the exact shift position of the pseudo-noise sequence by using Scilab and Xcos.
5. Simulation of Q-Channel and Analysis
We have taken the spreading factor![]() . Thus the signal is composed of 16384 (128 × 128) chips in order
. Thus the signal is composed of 16384 (128 × 128) chips in order
to encode the 128 information bits. The used data rate is 9600 bps (bit per second) and the chip rate is 1, 2288 Mcps.
Figure 7 shows the model designed under Scilab for the Q-channel, in very simple manner, it illustrates a DSSS process. It includes the MSRG with a mask and an RS-232 coding; with the transformation![]() ; where
; where ![]() is the value of the signal on a chip .
is the value of the signal on a chip .
Figure 8 represents frequency spectra of the information signal and the spread signal using Fast Fourier Transform (FFT).
The central band frequency band has been enlarged in a factor equal to the spread ratio![]() .
.
The spread spectrum is performed by acting on the parameters of the clocks. To have a spreading factor equal
to![]() , the clock connected to the PN is set to be 128 times faster than the clock connected to the
, the clock connected to the PN is set to be 128 times faster than the clock connected to the
shift register containing the information bits. This is a typical modeling of DSSS, each information bit is encoded by 128 chip of the pseudo-random sequence. Figure 8 is a comparison of the spectrum of the original information signal and the spectrum of the spread signal, under Scilab/Xcos. To get it we take the output from To workspace Blocks (info. values and signal. values). By this way, full spectral analysis can be made on systems such DS-CDMA.
6. Modeling a Gold Code Generator with Xcos
We take here two polynomials used for the Global Positioning System (GPS) and forming a preferred pair by the Gold criteria [7] : ![]() and
and![]() ; each one in Fibonacci configuration or SSRG. As it has been done for the MSRG, the conceptual model is shown in Figure 9. Figure 10 illustrates the designed model under Xcos. We denote G10 the output sequence of length
; each one in Fibonacci configuration or SSRG. As it has been done for the MSRG, the conceptual model is shown in Figure 9. Figure 10 illustrates the designed model under Xcos. We denote G10 the output sequence of length![]() .
.
6.1. Correlation of Generated Sequences
We take now ![]()
![]() as output for different initial loading of the first LFSR. By this way two gold sequences are obtained.
as output for different initial loading of the first LFSR. By this way two gold sequences are obtained. ![]() is the Auto Correlation function for
is the Auto Correlation function for![]() ; and
; and ![]() is the Cross Correlation of
is the Cross Correlation of ![]() and
and![]() .
.
6.2. Correlation of Gold Sequences
Figure 11 gives for ![]() a maximum value equal to 1023 and others equal to −65 and +65. The first one indicates that it’s the same sequence. The other peaks illustrate and confirm the defined value for the correlation of these kind of MLS. In a complete period, we have:
a maximum value equal to 1023 and others equal to −65 and +65. The first one indicates that it’s the same sequence. The other peaks illustrate and confirm the defined value for the correlation of these kind of MLS. In a complete period, we have:
![]()
![]() is the degree of the polynomial,
is the degree of the polynomial, ![]() and
and ![]() are two Gold Sequences.
are two Gold Sequences.
7. Discussion
Some studies have been made on the simulation of LFSR using Matlab and Simulink [8] . However, the method presented in this work use Scilab and offers many opportunities. The results in Figure 6 show one of them by getting the relative delay brought by the mask. These kind of analysis are related to multiple access in DS- CDMA systems [6] . Another contribution of our method is modeling, simulation and spectral analysis of other sequences generated by LFSR. In this category we can mention the Gold sequences generator Figure 10 offering
![]()
Figure 7. Q-channel PN-Generator, spreading simulation.
![]()
Figure 8. Amplitude diagram of information and spreaded signal.
indeed possibility to do the same for Kasami Sequences [9] . The flexibility of provided tools may also help to set up a test platform for Non Linear Feedback Shift Register (NLFSR) like De Bruijn sequences used for information security [10] .
8. Conclusion
This paper presents a simple, effective and efficient method for analysis of LFSR, used for CDMA; with computer algebra tool Scilab and Xcos. Advanced models of PN-Generator for I and Q channels are designed. This study provides very beneficial tools for applications related to spreading spectrum. A further study could take an interest in the hardware realization of proposed circuits.