1. Introduction
Recent advances achieved in radar technology and in methods for processing radar data are leading to increasing confidence in the use of radar-based rainfall estimates in hydrologic analyses and simulations. Accurate knowledge of catchment area rainfall amounts and spatial characteristics is crucial for flood forecasting and warning systems [1] - [4] , and can substantially improve the allocation of water resources for agricultural uses, as well as for hydroelectric production [5] . Further, accurate quantitative precipitation estimates from radar measurements can improve the understanding of the relation between point and areal rainfall [6] and improve definitions of annual rainfall intensity probability distributions used to estimate return periods of extremes (i.e., high rainfall rates), due to the large amount of data collected by the radar at each scan [7] .
Rainfall estimation has been an important part of radar research since radars were first implemented. Based on the Z-R relationship (Z = aRb), rainfall rate can be estimated from radar reflectivity. Here Z is the radar reflectivity, R is the rainfall rate, and a and b are empirical constants [8] [9] . Early research showed that while average optimal constants in the relation Z = aRb could be found, more appropriate values vary depending on location and weather type [9] [10] . Specifically, these variations in the parameters are caused by microphysical and kinematical processes that affect the drop-size distribution and fall speeds [9] [11] [12] . Even if a perfect Z-R relationship could be found for a particular spatial or time scale, other errors such as calibration, attenuation, bright bands, anomalous propagation, and range degradation affect the radar estimates [2] [11] . Numerous methods have been proposed to correct for one or more of these errors [11] [13] - [15] . [16] Created an algorithm that makes corrections for many of these errors by defining adjustment parameters for each type of error individually.
The main goal of this paper is to examine rainfall amounts associated with flash flood occurrences over Jeddah on 25 November, 2009 using radar data and the Z-R relationship. Radar stations have been installed in Saudi Arabia for a couple of years such that the active radius covers the whole area of the country. Therefore, rainfall detection from radar information is a highly promising and practical approach to estimating rainfall. Since, the rainfall (R)-radar reflectivity (Z) could be expressed in linear or empirical power function, the investigation of characteristics of Z-R relationship for the flash flood area was undertaken. In our study we used the Jeddah radar station located in the Northern part of Jeddah airport. The installed radar in this station is Doppler radar with an active radius of 120 km. The rainfall event of 25 November 2009 was analyzed for Z-R relationship. In this study the Spatial Probability Technique (SPT) analysis has been used. This technique was developed based on the GIS basic function and the probability matching method. Using this technique, Z-R pairs can be analyzed for both linear and empirical power relationships. However, this research is an investigation of the Z-R relationship; the warning system development needs further study of other parameters relevant to rainfall and flash flood occurrence.
2. Reflectivity-Rainfall Relationship
The Z-R relationship can be described by the empirical power law relationship [17] [18] , which can be expressed as:
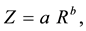 (1)
(1)
where a and b are coefficients that depend on location and climatological factors such as season, type of rain. These coefficients are independent of the rainfall itself. However, the Z-R relationship can be expressed in linear Z-R relationship for equilibrium rainfall condition as steady tropical rain [19] [20] presented that the Z-R relationship should be used differently according to precipitation types to reduce the uncertainty of rainfall estimation. [1] suggested that different parts of a storm have significantly different relationships. [21] showed that Z-R relationship was different depending on the type of precipitation and suggested a relationship of Z = 300 R1.37 for the convective rainfall and Z = 205 R1.48 for stratiform rainfall based on case studies.
3. Matching Process
From past research, several matching procedures between reflectivity (Z) and Rainfall (R) have been proposed such as: Traditional Matching Method (TMM), Probability Matching Method (PMM), Window Probability Matching Method (WPMM) and Window Correlation Matching Method (WCMM) [22] - [26] . In all process except TMM, the matching is done between the Cumulative Distribution Functions (CDFs) of Z and R as described in Equation (2) and Figure 1.
 (2)
(2)
P(R) is the probability density function of rainfall from gauge measurement and P(Z) is the probability density function of radar reflectivity. The matching of Z and R is done at the same probability level. Two techniques of Spatial Probability Technique (SPT) and Buffer Probability Technique (BPT) are proposed.
In this study we used SPT; SPT is the process using the basic GIS interpolation function to estimate radar reflectivity over the rain gauge station at the measurement time. In this process, it is assumed that raindrops fall vertically downward. As rainfall (R) is the measured rainfall at time t for a rain gauge location, the reflectivity (Z) can be calculated by Kriging interpolation from the surrounding measured reflectivity data at time t. Then, for any time t, the corresponding data of Z-R can be obtained. The matching is done by probability matching as in equation 2 above to avoid the timing error.
BPT is a procedure developed to decrease the error from wind effects that cause raindrops to not vertically fall into the rain gauge. BPT uses the basic GIS buffer function to estimate the radar reflectivity over the rain gauge station at the same time. The Z value, which corresponds to the R value at time t can be calculated from the arithmetic mean of Z values detected at time t within a 1-km buffer area above the rain gauge. Then, the matching is done as before by probability matching. Figure 2 illustrates the SPT and BPT procedures.
4. Data Description
A) Radar data
The radar measurements used in this study were collected during November 2009 to June 2010at Abha in the south of Saudi Arabia located at 18.22˚N, 42.66˚E on a 2105 m plateau. They were made as part of a rain enhancement project of the Presidency of Meteorology and Environment (PME) with National Center of Atmospheric Research (NCAR). The three dimensional radar scans cover the entire volume of the troposphere in the 20 to 120 km range every 5 min. The radar has a 5.3 cm wavelength, C band and pulse width of 0.8 mu. For verification, we used the measurements of the Jeddah radar in the west of Saudi Arabia located at 21.71˚N, 39.18˚E on an 18 m plateau with same type of radar as in Abha.
B) Gauge rainfall data
The rain gauge measurements used in this study is the only high-resolution tipping bucket rain gauge with remote SIM-card and solar panel located at Abha (18.29˚N, 42.35˚E) in the south of Saudi Arabia at 2876 m altitude (Figure 3). The Abha rain gauge was established as part of a rain enhancement project of the PME with NCAR. For verification we used the Jeddah rain gauge, where the available data period used for the calibration
![]()
Figure 2. SPT and BPT diagram over the rain gauge location.
of the Z-R relationship is from November 2009 to June 2010. The Jeddah station operated by PME is within the Jeddah radar radius (Figure 4). Also we used two other rain gauges: the first one is at (21˚30'E, 39˚12'N) while the second one is at (22˚49'E, 39˚02'N). They are operated by the Ministry of Water and Electricity (MOWE).
C) TRMM data
For this study we use the TRMM 3G68 version 5 data products, which consist of rain-rate retrievals from instantaneous fields-of-view (IFOVs) of the TMI and PR that are area-averaged over 0.5˚ ´ 0.5˚ longitude-latitude grid boxes (~50 km ´ 50 km in the Tropics).The 3G68 data are not time averaged beyond the short time required for the instrument swaths to sweep through a 0.5˚ ´ 0.5˚ box. As mentioned earlier, there is some implicit time averaging in both retrievals related to the fact that surface rain rates are inferred from precipitation information at altitudes above the surface. For simplicity, TRMM rain retrievals without explicit time averaging (that is, individual overpasses) will be referred to as instantaneous rain rates.
5. Studied Process
The rainfall from automatic rain gauges was measured continuously where every pulse is equal to 0.2 mm, while the reflectivity from radar was measured every 5-min. In this study the Spatial Probability Technique (SPT) analysis has been used. This technique was developed based on GIS basic function and probability matching
![]()
Figure 3. Position of rain gauge from the radar.
![]()
Figure 4. Position of rain gauge from Jeddah radar.
method. Using this technique the Z-R pairs can be analyzed for both linear and empirical power relationships. The 5-min rainfall was normalized by aggregating into hourly rainfall with the same time interval as the radar measurements. The Z-R relationship investigation is summarized in Figure 5.
6. Synoptic Discussion
On November 25, 2009, heavy rainstorms hit Jeddah, Makah and other regions in western Saudi Arabia. More than 90 millimeters of rain fell in Jeddah in just four hours. This amount is nearly twice the average for an entire year and the heaviest rainfall in Saudi Arabia in a decade. A case of winter cyclogenesis over the Mediterranean is considered in the present study extending from 23/12 to 26/12 November 2009. 1000 hPa and 700 hPa charts for each 6 hours of the period 24/06 to 26/00 are shown in Figure 6 and Figure 7 respectively. 1000 and 700 hPa charts depict contours of height with 10 geopotential meters (GPM) increments.
The isotherms in the charts of the two levels are analyzed with 2˚C increments. On 23/12 November the subtropical high pressure dominates over North Africa and the Mediterranean area; it also extends easterly to cover the north of KSA and east Mediterranean countries (not shown). The Sudan low and its associated inverted v- shaped trough (Red Sea trough) oscillate northward to cover the east of Egypt and the entire Red Sea region. An obvious thermal gradient associated with the northward oscillation of Red Sea trough extends zonally to cover the south of KSA and the north of Sudan. On 24/06 the subtropical high weakens and moves eastward, while the Red sea trough propagates slowly northward and the Sudan low deepens to 80 gpm (Figure 6(b)).
![]()
Figure 6. 1000 hPa height contour in 10 m intervals (solid) and temperature (dotted) in 2˚C increments for 24/06-26/00 UTC November 2009.
![]()
Figure 7. 700 hPa height contours in 10 m intervals (solid) and temperatures (dashed) in 2˚C increments for 24/06-26/00 UTC November 2009.
At 700 hPa the cyclone of special interest appeared as an extension of the traveling depression east of the Mediterranean at 24/06 where a cut-off low is formed and a well-defined cyclonic depression becomes clear over north Egypt (Figure 7(a)). On 24/12 the Sudan low at the surface and its associated Red Sea trough moves northward to cover the north of the east Mediterranean, Egypt and east of KSA where the center of the low becomes over Red sea at 18oN and 39oE while the geopotential height at the center reaches 100 gpm. In the upper air (700 hPa) the cut-off low deepens and moves slowly eastward to a point just northeast of Egypt; the geopotential height at the center reaches 3080 gpm (Figure 7(b)).
During the period 24/18 to 25/12 November (the rainy period), a strong interaction occurs between the inverted v-shaped troughs extending from the tropical region and from middle latitude region, the two cyclones join. The most interesting features are the strong northward warm advection from the tropical region associated with the air flow around the Sudan low and the strong southward cold advection. The interaction between these two air masses causes a strong instability over the east of Mediterranean and at the west of Saudi Arabia.
After 25/12 November, the inverted v-shaped trough of the Sudan low moved southwest ward while the upper air trough retreated westward and the interaction between the two troughs vanishes. During the next day (26 November) the depression starts to weaken and its central pressure increases gradually. On the other hand, the subtropical high pressure over North Africa and the western Mediterranean is extended with a major ridge that joint the Siberian high. While the Siberian high pressure propagates westward at the surface, the horizontal extension of the cyclone at 700 hPa decreases and moves slowly eastward. It becomes a stationary vortex rotating above the northeast of Mediterranean (Figure 7(g), Figure 7(h)). Finally the cyclone drifts slowly northeastward and leaves the area by 28 November.
7. Results and Discussion
The aim of this study is to find new Z-R relationships suitable for this area; the resulting relationships will be used to improve radar estimates of rainfall. Finally, the deduced relation will be verified and applied to the case of flooding in Jeddah on November 25, 2009.
7.1. Z-R appropriate Constants
The radar-estimated rainfall rate was calculated using the Z-R equation of [17] which is Z = aRb, and compared with 5-minute rainfall accumulations measured from the gauge. Figure 8(a) shows scatter plots of the 5-minute rainfall accumulations measured from the gauge and the radar data. The radar rainfall is obtained using the relation Z = 200 R1.6 has little correlation with the 5-minute gauge data and systematically underestimates the rainfall amounts. The systematic underestimation can be removed by applying a multiplicative bias correction factor. The multiplicative bias changes the multiplicative coefficient of the Z-R relationship and essentially creates a new Z-R relationship. It does not change the exponent of the Z-R relationship. Hence, a bias correction is equivalent to new Z-R relationship.
A new Z-R relationship that reduces the underestimation can be developed from the data. Also, as a result
![]() (a) (b)
(a) (b)
Figure 8. (a) Linear Z-R relationship, a = 200; (b) Linear Z-R relationship, a = 150.
from the previous studies [25] of a case of convictive clouds, the constants a and b had been changed and the following Z-R relationship is found as optimum:
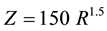 (3)
(3)
where R is the rainfall rate in mm/hr and Z is the reflectivity in mm6/m3. It is clear from Figure 8(b) that the value of correlation coefficient of rainfall improved which improves the ZR relationship, and then we choose the relationship ZR over our area is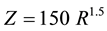 .
.
As a result of the above discussion we decided to use Equation (3) to calculate radar rainfall. In the following we try to improve the results by, first applying the equation on hourly and five minute data and compare the result, and secondly, by considering the effect of mountain clutter.
7.2. Comparison between Hourly Data and Data of 5 Minutes
The 5-minute gauge accumulations are converted to the equivalent rainfall intensity in mm/hr. The developed relation has been applied to the hourly data and also for 5 minute data. Figure 9(a) illustrates the correlation between the hourly rain gauge data and hourly radar data for the same time, while Figure 9(b) show the correlation between the 5-minute rain gauge data and 5-minute radar data for the same time. The comparison between the two figures illustrates that the correlation coefficient for hourly data is better than that for 5-minute data. This is due to the sensitivity of the data affected by weather factors such as the mountain or wind [27] . To verify that the hourly accumulations show a significantly improved correlation between gauge and radar data the previous step had been applied by using Z = 200 R1.5. Figure 10 shows scatter plots of the gauge and the radar data in the case of hourly accumulations and 5-minute accumulations, respectively. The correlation coefficient for the two cases is 0.46 and 0.03, respectively, which is a significant improvement. Using hourly resolution apparently smoothens out sampling errors due to the temporal mismatches between the two datasets.
7.3. Effect of the Mountains
Radar signals may be partially intercepted by ground targets (e.g. buildings, towers) and this source of error is known as “ground clutter” [28] . If the beam is completely blocked by mountains, it is known as “beam blockage”. The small changes in the beam propagation affect the presence of clutter echoes, or where the returned signal is at the threshold level. The estimation values were affected by the nearby mountains. Figure 11 shows the radar reflectivity taken in clear air shows the ground clutter at different heights. The implication is that this affects the radar estimates throughout the day and the heights, where it’s clear this noise affect the data from height 0 to 4 km.
We filtered the data to solve this problem by basing our calculation on data from 4 km and above. Then, we re-processed the data calculations by using this condition on the hourly data. Figure 12(a) shows scatter plot and the correlation with clutter (before treatment) while Figure 12(b) shows the scatter plot and correlation with
![]() (a) (b)
(a) (b)
Figure 9. (a) Linear Z-R relationship, a = 150, 1Hr data; (b) Linear Z-R relationship, a = 150, 5 min data.
![]() (a) (b)
(a) (b)
Figure 10. (a) Linear Z-R relationship, a = 200, 1Hr data; (b) Linear Z-R relationship, a = 200, 5 min data.
![]()
Figure 11. Radar reflectivity with the height.
non-clutter (4 km and above). The comparison between Figure 12(a) and Figure 12(b) illustrate that the relationship improved after this treatment.
7.4. Choose the Best of 9 Pixels
As illustrated in Figure 13, we designed a simple grid system for the rain gauge network to effectively position rain gauges within specific scale pixels. The 0.75 km grid boxes in Figure 13 are all sub-pixels of a 2.25 km grid, and all gauges are included within the 2.25 km scale.
For the true area-averaged rainfall, we computed the simple average of the corresponding rain gauge data within each gird box. Also, the maximum values of 9 pixels have been obtained. The results of Z-R correlation using the average value of 9 pixels is illustrated in Figure 14(a), while Figure 14(b) shows the Z-R correlation using the maximum values. Comparing Figure 14(a) and Figure 14(b) shows that using the maximum values has higher correlation than using the average values, which may be due to thunderstorm precipitation, where the effect of such these cases is very limited in areas [29] .
The final result of our previous experiments is that the relationship of Z-R Equation (3) is the best formula to apply in this case. Figure 15 shows the final correlation using the constants a = 150 and b = 1.5, hourly data, filtering data (without clutter), maximum values of the 9 pixels.
![]()
![]() (a) (b)
(a) (b)
Figure 12. (a) Linear Z-R relationship, a = 150, 0 to 30; (b) Linear Z-R relationship, a = 150, 4 to 30.
![]()
Figure 13. The grid system for the rain gauge.
![]() (a) (b)
(a) (b)
Figure 14. (a) Linear Z-R relationship, a = 150, mean values; (b) Linear Z-R relationship, a = 150, max values.
7.5. Validation for the Case Study
In terms of parameterization of the radar data processing (the previous step), we obtain for an optimization-based approach aimed at defining a single effective Z-R relationship by comparing the radar and rain gauge rainfall amounts at the event time 25 November 2009 scale in the region hit by the rain event. We chose the two rain gauges where, firstly as already mentioned, rain gauge data are generally available for flash flood events at this time. Secondly, the position of this rain gauge is out of blind spot compared with airport station.
The developed relation (a = 150, b = 1.5) has been applied on the Jeddah radar dataset and accumulated the data to be in 24 Hr format at a case study period time and then change the relation (a = 200, b = 1.6) and the reprocessing of data. Figure 16 illustrates the daily values of rain gauge and the radar rain estimation when applying the Z-R relation with a = 150, b = 1.5 and with a = 200, b = 1.6. It is found that a good agreement occurs between rain gauge with radar estimation when a = 150, b = 1.5.
The Jeddah rain maps for 25 November 2009 were accumulated for 24Hr where the rain maps (Figure 17) illustrate the spatial rainfall pattern sampled by the Z = 150R1.5. Figure 18 illustrates the spatial rainfall pattern of TRMM data of 25 November 2009; it is clear that the comparison between two figures shows a good agreement between the two patterns.
8. Conclusions
The operational use of weather radar has become a widespread and useful tool for estimating rainfall fields. The radar-gauge adjustment is a commonly adopted technique, which allows one to reduce bias and dispersion between radar rainfall estimates and the corresponding ground measurements provided by rain gauges.
The aim of this study was to find new Z-R relationships suitable for our area of study; the deduced relationship is based on the collected radar measurements at Abha during the period from November 2009 to June 2010. The final result of our experiments is that the best relationship of Z-R is Z = 150R1.5 under using constant a = 150 and b = 1.5, hourly data, filtering data (without clutter), maximum values of the 9 pixels. The deduced relation (Z = 150R1.5) has been verified and applied to our case of study (the case of Jeddah 2009). A good agreement occurs between rain gauges with radar estimation. We also find that the rainfall pattern location and shape
![]()
Figure 15. Linear Z-R relationship, a = 150 ,1Hr data, 4 to 30 , max values.
![]()
Figure 16. Compared chart between rain gauge and radar rainfall (a = 200, 150).
![]()
Figure 17. Map of rainfall from Jeddah radar.
![]()
Figure 18. The spatial rainfall pattern of TRMM data of 25 November 2009.
sampled by the Z = 150R1.5 are in close agreement with the corresponding of TRMM data of 25 November 2009. So, it is found that empirical power function is more appropriate to describe Z-R relationship than linear function for the studied area. However, this research is just the early state of Z-R relationship investigation; the warning system development needs further study on the other parameters that relevant to rainfall and flash flood occurrence.
Acknowledgements
The authors would like to acknowledge the support of the King Abdulaziz University (KAU) and the Presidency of Meteorology and Environment in Saudi Arabia (PME). The NCEP data are obtained from their website.