1. Introduction
Research needs to address the climate change impacts of problems using hydrological models include estimates of scaling parameters, model validation, generation of climate scenario, and data, and modular modeling tools to provide a framework to facilitate interdisciplinary research. Solutions to these problems would significantly improve the ability of models to assess the effects of climate change [1] .
Assessment of seasonal and long-term water availability is not only important for sustaining human life, biodiversity and the environment, but also helpful for water authorities and farmers to determine agricultural water management and water allocation. Climate change is one of the greatest pressures on the hydrological cycle along with population growth, pollution, land use changes, and other factors [2] . Water availability is under threat from changing climate because of possible precipitation decrease in some regions of the world. In the light of the uncertainties of climate variability, water demand, and socio-economic environmental effects, it is urgent to take some measures to use the limited water efficiently and develop some new water resources [3] . If the water resources are replenished by snow accumulation and the snowmelt process, the water system will be more vulnerable to climate changes [4] .
Many studies have evaluated climate change impacts on stream flow including spatial components of water availability by using various modelling methods across the world climates [5] -[13] . In this paper, House-Peters, L. A., and H. Chang [14] , a theoretical framework of coupled human and natural systems is used to review the methodological advances in urban water demand modeling over the past three decades. This review begins with coupled human and natural systems theory and situates urban water demand within this framework, reviews urban water demand literature and summarizes methodological advances in relation to four central themes: interactions within and across multiple spatial and temporal scales, acknowledgment and quantification of uncertainty, identification of thresholds, nonlinear system response, and the consequences for resilience, and the transition from simple statistical modeling to fully integrated dynamic modeling. This review will show that increasingly effective models have resulted from technological advances in spatial science and innovations in statistical methods. These models provide unbiased, accurate estimates of the determinants of urban water demand at increasingly fine spatial and temporal resolution.
Climate impacts on water resources are varied in different river basins. The frequency of droughts and floods will increase under future climate conditions. Runoff and streamflow are more sensitive to rainfall than to evapotranspiration. Efficient water use and integrated management will be increasingly important for reducing the impacts on water scarcity and droughts. Although many water management approaches have been adapted to mitigate climate impacts, there is still a need to determine local solutions. It is necessary to know how much water can be used in each irrigation area and the river basin, when the water is available and how much water can be stored for use in the drought period, variability quantity of water resources over a long-term basis and associated links with energy and biodiversity.
The aim of this study is to develop a statistical model to predict the future of urban water consumption as a result of climatic changes, to develop a better understanding considering factors of economic and climatic.
2. Methodology
For this study, the consumption region of Aquidauana city was chosen with average daily water consumption of 381 liters/day. Temperature is one of the factors that can influence water consumption [15] . For this reason, monthly temperature data (average, minimum and maximum), relative humidity (average, minimum, and maximum), wind speeds, precipitation, coefficient of seasonality, number of water consumers and water consumption from January 2005 to 2014 were obtained from SANESUL System (Water Systems of South Mato Grosso). The meteorological data were provided by the Water Resources Monitoring Center of South Mato Grosso― CEMTEC.
Aquiduana is located in the south of the Midwest Brazilian region, in the Pantanal of South Mato Grosso (wetlands), micro-region of Aquidauana. It is located at latitude 20˚28ꞌ15" South and longitude 55˚47ꞌ13" West, at an altitude of 149m. It is situated between the Piraputanga and the Maracaju mountain ranges. Its territory is divided into two parts: the low one (two-thirds of the town) and the high one in the mountain ranges).
The tropical climate of the region, with an annual average of 27˚C, features two opposing moments. The period between October and April is marked by floods and high temperatures. While from mid-July to end of September, it is represented by a period of drought, with frosts and milder temperatures of approximately 15˚C. It occupies an area of 16 958.496 km2.
3. Multiple Linear Regression
SPSS (Statistical Package for the Social Sciences) and Table Curve softwares were used to perform the statistical analysis. The intervening variables were entered as independent and water consumption as the dependent variable.
For the processing of data, the following resources were used: descriptive statistics, correlation analysis, development of scatter plots, hierarchical clustering analysis of main components, and finally, statistical modeling and model validation based on residual analysis.
Regarding the statistical model, the existence of a reasonable number of intervening variables guided the use of multiple regression analysis and correlation as limiting indicator of the participation of these variables in the model. Therefore, the explanatory variables in the model were considered, those with higher correlation coefficients. From the reduced variables, Table Curve software located the possible models as well as presented the statistical parameters and waste. The multiple linear regression model can be illustrated as Equation (1) below:
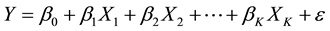 (1)
(1)
where 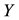 is the dependent variable;
is the dependent variable; 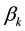 are the coefficients;
are the coefficients; 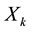 are the independent variables and
are the independent variables and 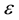 is the deviation error.
is the deviation error.
The Seasonal coefficient indicator (SC) includes the effect of seasonality on models and here it was calculated by the ratio between the measured volume of the month by the average of the measured volume of the year, as seen in Equation (2):
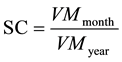 (2)
(2)
3.1. Statistical Analysis
In this study a descriptive analysis of the variables shall be done and, subsequently, the hypotheses will be tested using multiple regression models. The root mean square error (RMSE) has been used to verify the accuracy of the model.

where: 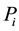 is the estimated value and
is the estimated value and 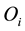 the observed value. In all analyses, a tolerance level equal 5% was considered.
the observed value. In all analyses, a tolerance level equal 5% was considered.
3.2. Main Component Analysis (ACP)
Multivariate analysis techniques, like ACP techniques, are powerful tools when analysing a great number of variables. They allow a reduction of the observation matrix dimension without losing the important pieces of information of the original data, enabling thus further investigation of the time-space behaviour of the variables involved in the problem, as well as detecting groups of variables that present homogeneous behaviour. This method has the objective of describing data contained in an individual-numerical character matrix: characters p are measured in n individuals.
Basic information gathering, in main component analyses, is the data matrix. In n observations there are m variables, so the normalized data matrix (with zero mean and one variance) of the wind speed can be presented as m ´ n, and indicated by Z, from where the correlation matrix R, given in Equation 1, can be obtained.
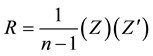
where 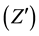 is the transposed matrix of Z. R is a positive symmetric matrix of (k ´ K) dimension; it is diagonalizable by an A matrix, of base change, denominated eigenvector. The diagonal matrix D whose diagonal elements are the eigenvalues (λ) of R is expressed by:
is the transposed matrix of Z. R is a positive symmetric matrix of (k ´ K) dimension; it is diagonalizable by an A matrix, of base change, denominated eigenvector. The diagonal matrix D whose diagonal elements are the eigenvalues (λ) of R is expressed by:
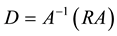
Due to the eigenvector orthogonality, the inverse of 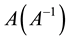 is equal to its transpose
is equal to its transpose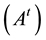 . Therefore, main components (MCs)
. Therefore, main components (MCs) 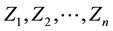 are obtained through linear combinations between the eigenvectors transpose
are obtained through linear combinations between the eigenvectors transpose 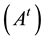 and the observation matrix
and the observation matrix![]() , i.e.:
, i.e.:
![]()
![]()
Each line of Z corresponds to an MC that forms the temporal series associated to the eigenvalues. Values of Y in the n-th local may be calculated by:
![]()
The solution to this equation is unique. It considers the total variation present at the initial variable group, in which MC1 explains the maximum possible variance of the initial data, whereas MC2 explains the maximum possible variance still unexplained, and so forth, until the last MCm which contributes with the smaller parcel of explanation to the total variance of initial data.
In the case of this study, every MC has a portion of the total variance of wind speed monthly data, and they are arranged in decreasing order of the most significance eigenvalues of a1 in A, given by.
![]()
Total variance of the system (V) is defined as the sum of the variances of the observed variables; therefore, V is given by:
![]()
where S is the variance of observed variables, and λᵢ are the eigenvalues. The matrix trace can be understood as well as the total sum of the main diagonal of the correlation matrix.
The variance explained by each component is:
![]()
The chosen number of MCs was based on the Kaiser truncation criterion, which considers as the most significant eigenvalues those values which are superior to the unit.
3.3. Groupings Methods (Cluster)
There are two types of methods or group classification algorithms. One is the hierarchical method, in which the partition of the groups starts from a minimum of groups not initially defined. The major groups are divided into minority subgroups grouping those individuals who have similar characteristics. The final structure of classes is presented as a classification tree (dendrogram) having an objective summary of the results. The other is a non- hierarchical method of classification in which the number of groups is set a priori. In both clustering methods, classification of individuals into different groups is made from a grouping function and a mathematical grouping criterion [16] [17] .
3.4. Ward’s Method
This is a hierarchical method which uses Euclidean distance to measure the similarity or dissimilarity between the individuals, that is, the distance between Xi and Xj individuals is given by [16] :
![]()
Ward proposes that at any stage of the analysis the loss of information, which results from the grouping of individuals into clusters, is measured by the total sum of squared deviations (SQD) of every point from the mean of the cluster to which it belongs [16] .
![]()
where n is the total number of the elements of the grouping and xi is the ith element of the grouping.
4. Results and Discussion
4.1. Consumption Profile
The survey of the average monthly consumption, in turn, showed that it varies throughout the year, being higher in the summer, peaking in January and lower in the winter, especially July. In general, the trend in consumption is to decrease from the month of March on and increase from the month of November on. The month of August has a peak compared to the winter months, a result of dry weather that occurs during this period, which causes an increase in consumption. During the week, Sunday is the day of lowest consumption and Friday the highest. Wednesdays and Saturdays are days close to the average consumption.
The same may occur in relation to consumption throughout the day. In general, the peak consumption takes place from 12:00 p.m., when it becomes more or less constant, with minor variations until 5:00 p.m. Then, it begins to decrease at about 6:00 p.m., becoming nearly constant over the period between 9:00 p.m. and 12:00 a.m. The period between 1:00 to 6:00 a.m. shows a reduction in consumption, and the minimum occurs at 6 o’clock in the morning. After this period, it starts to increase again.
We used 3285 observations, whose variables were classified according to the class, month, seasonality, rainfall (rain), temperature (Temp), relative humidity (RH), wind speed, and number of consumers. The statistical validation sample (n) was effected by calculating the size of stratified random sample for average estimates for finite population [14] . Calculations indicated that n of 365 observations would be enough; however, the performed was higher than ideal n for statistical validation. Therefore, it was deduced that the sample was statistically representative. Statistics was used in order to prove that the sample was representative.
Descriptive statistics are presented in Table 1. Note that the average values of per capita water consumption of 156.6 L/inhabitant per day are no different from the national average, where the consumption is 150 L/inha- bitant per day.
Positive and negative weak correlations concerning the variables were observed. The graphical representation of quantitative variables allowed understanding the joint behavior of the variables as to whether or not there is the association between them. A very useful device to verify that association is the scatter plot [15] .
Referring to Figures 1-3, they show a lack of interaction between the variables, then suggesting the null association between the air temperature variables, rainfall, wind speed and relative humidity with water consumption. This result was also confirmed according to Table 2, in which extremely low correlation coefficients were observed. By comparing this result with the classical literature, there was a local specificity: the nullity of correlation between climatic variables and the demand for water. One of the possible explanations is based on seasonality, with two well-defined periods in the region and low temperature variability [18] .
The graphical analysis of Figures 1-3 presented correlation trends, since they show increasing linear trend and formation of dispersion clouds, respectively. ViannaI, V. and Depexe, M. D. [19] , by using different variables of distinct time series, for the city of Umuarama-PR, a mathematical model of multiple regression for water consumption was employed, and it was possible to simulate forecasts, and with its results, make comparative
![]()
Table 1. Descriptive statistical analysis of the variables to the city of Aquidauana from 2005 to 2014. Temperature (˚C), humidity (%), wind speed (m/s), rain, water consumption, number of consumers, seasonality coefficient and estimated value of annual average consumption of water (m3/s).
![]()
Figure 1. Seasonal variation of the average monthly volume of water observed and estimated according to the months of the years 2005 to 2014 in Aquidauana.
![]()
Figure 2. Histogram and waste of the estimated values for the water consumption in the period from 2005 to 2014 in Aquidauana.
![]()
Table 2. Correlation coefficients of the variables analyzed in Aquidauana.
Significant correlation is noted at the 0.01 level.
![]()
Figure 3. Observed and estimated values for water consumption (m3/months) in Aquidauana, period from 2005 to 2014.
analyzes. Thus, the accuracy and errors obtained were analyzed. At the end of the study, an equation capable of predicting the volume of consumed water from Umuarama with acceptable errors was reached.
Lins et al., [20] , utilized the multivariate techniques Factor Analysis and Multiple Linear Regression Analysis―in order to determine the participation level of socioeconomic and climatic variables in monthly urban household consumption changes―applying them to two districts of Campina Grande city (State of Paraíba, Brazil). For both the selected districts of Campina Grande city, the obtained results point out the variables “water tariff” and “family income” as indicators of these district’s household consumption.
The scatter plot, shown in Figure 3, presented dispersing clouds of different trends in behavior between the variables of water consumption, which suggested the existence of groups with specific characteristics of consumption of these resources.
Daily urban water consumption in Aquidauana from 2005 to 2014 was modeled and the statistical model developed explains 71.5% of the variance with the following three factors: number of consumers (19.3%), seasonality (37.8%), and climate regression (14.3%). The model was further validated using an independent set of data from January 2014 to August 2014, yielding an R2 of 86%. The results indicated a good performance of the statistical model developed to describe the temporal variations of the use of urban water in Aquidauana.
Considering also the selection of the intervening variables in water demand, a cluster analysis was performed, which is a set of statistical techniques whose aim is to group objects according to their characteristics, forming groups or homogeneous clusters [15] . Hence it is possible to infer about the number of clusters and which variables are grouped together. In this case, three clusters can be observed. The constituent variables of the first cluster were seasonality; on the second cluster, trend and number of consumers; on the third the temperature, wind speed, rain and humidity.
Wong; J S; Zhang, Q, Chen, YD [21] , sought to address statistical properties and urban water consumption forecasts daily in Hong Kong from 1990 to 2007. A statistical model was designed to differentiate the effects of five factors in water use, i.e., trend, seasonality, climate regression calendar effect, and auto regression. The statistical model developed explains 83% of the variance of six factors: tendency (8%), seasonality (27%), climate regression (2%), days of the week effect (17%), the holiday effect (17%), and automatic regression (12%). The model was further validated using a set of independent, producing an R2 of 76%.
Studies between detrended seasonal urban water use and weather and climate variables (precipitation, maximum temperature) is examined at daily, monthly, and seasonal scales using stepwise multiple regression and autoregressive integrated moving average (ARIMA) models. At a seasonal and a monthly timescales, interannual variation in maximum temperature is the most important predictor of seasonal water consumption per capita, explaining up to 48% of the variation in seasonal monthly water consumption. At a daily scale, one-day lagged seasonal water demand and maximum temperature are the variables that are significant in all the daily models. Together with day of the week and precipitation, these variables explained up to 87% of the variation in seasonal daily water consumption in summer. ARIMA models that take into account temporal autocorrelation explain between 70 and 81% of daily seasonal water consumption in summer months [22] .
Concerning the selection of variables―a statistical model using regression techniques was developed. Then, the statistical model presented in the following multiple linear equation was obtained. The coefficients of the model at a significance level at 1% probability level for the F test were the following: a) Aquidauana: linear coefficient = −155,517; maximum temperature = 118; minimum humidity = −74; wind speed = −297; rain = 4.8; number of consumers = 13.4; seasonality = 130,186 and error = 1.7% and R2 = 0.865.
The verification of the adequacy of the model was performed using residual analysis in Figure 2 and Figure 3 for waste normality and histogram, respectively. The p x p chart for waste normality indicates the presence of discrepant elements and groups resulting, a priori, from the existence of subgroups within the classes, or even measurement errors; hence, an investigation of the possible causes of the deviation is suggested.
By analyzing the histogram, it was concluded at first that the waste presented normal distribution since the frequencies appeared close to the normal distribution curve. However, the Kolmogorov-Smirnov test did not confirm the hypothesis of normality. After the waste was analyzed and a violation of the initial assumptions was diagnosed, the verification of possible biases is recommended for the model to fit the data and the assumptions made.
There is a positive relationship consumption of water and temperature and inverse relationship with precipitation [14] ), but few previous studies have examined how the temporal scale of analysis affects these relations. Maidment and Miaou [23] found that daily base use is sensitive to days of the week and that daily seasonal use exhibits a relation to certain climate thresholds, meaning that there are particular daily maximum temperatures at which water use exhibits a step change. Below these thresholds, however, water use and temperature may exhibit linear relations. They divided water use into base use, defined as primarily indoor use independent of the influence of climate, and seasonal use, which is climate dependant. Seasonal use is calculated by subtracting the base use, often estimated by using the average water use for the lowest-use month, from the total use [24] .
The study of water use has been made in seasonal or daily variations [21] [23] [25] or monthly seasonal use only [25] [26] . Water consumption research is typically constrained by a lack of detailed long-term data to draw from. Many previous studies typically used only a few years of data [27] -[29] , not fully taking into account interannual climate variability. This limits the utility of developed models for forecasting future water demand.
To draw meaningful inferences on water consumption as it relates to weather and climate variability, multi- scale analysis is needed. Multi-scale temporal analyses allow us to project short-term and long-term water demand based on the fluctuations of climate variables, namely temperature and precipitation. Water resource managers need not only seasonal climate but also daily weather information as they relate to water supply and demand, and may need to identify the most important variables for short-term operational (i.e. daily, weekly) and mid- to long-term tactical or strategic (i.e. monthly, seasonal, yearly) planning [30] -[34] . Most previous studies used diverse methods ranging from regression-based analysis to artificial neural network. While some of these sophisticated methods may provide accurate water demand forecasting, they are mathematically complex and require fine scale weather data (e.g., sub-daily). Additionally, some of these studies heavily rely on detailed socioeconomic characteristics of customers (e.g., household income, size of house, etc.) to derive the parameters of water demand model coefficients. Moreover, since water use can fluctuate day by day, using the raw water use data may not be suitable for identifying the determinants of water use at a finer temporal scale.
4.2. Validation of the Model
The validation of the model was performed by relative error method [29] . Figure 2 is the histogram of relative errors of daily water consumption calibration, indicating that 86.5% of model estimates fall within the relative error band 1.7%. The modeled daily total water consumption is compared with the observed daily water consumption (Figure 1). Figure 3 indicated a suitable relation between observed and modeled water consumption with R2 of 86.5%. An independent check was conducted using daily water consumption for Campo Grande from 1 January 2005 to 31 December 2014 (Figure 1). In this validation period, 86.0% of the daily estimates are within error band ±1.7% (Figure 1 and Figure 2). Figure 2 showed that the modeled daily urban water consumption could well capture the major properties of observed water use variations. To evaluate quantitatively the performance of the statistical model, we analyzed the correlations between observed and modeled water use series (Figure 2). The results indicated that the modeled daily urban water consumption explained 71.5% of the variance of the observed daily urban water use of Campo Grande. Thus, the statistical models we developed in this study have reasonably adequate performance in describing the observed daily urban water consumption variations.
5. Conclusions
It was observed that there was an average value of per capita water consumption in the regions of 175 L/inhabi- tant per day, which is a number consistent with typical values for community size [35] . As a positive point, we can highlight the inference on a regional specificity, the non-intervention of climatic factors in per capita water consumption, which differs from the classical literature. One of the possible explanations is based on local seasonality, with two well-defined periods in the region and low temperature variability [18] .
In addition, the premise of the correlation between water consumption and socio-economic factors can be confirmed, which is a hypothesis of significant differences in the distribution of water consumption due to the different socio-economic conditions of the population. It is recommended that further investigation is directed to adjustments to the model proposed by insertion and interaction of economic variables and holiday periods.
The use of models to meet the management of water resources brings the perspective of a useful tool that can assist in the expansion and regulation of water supply, assuming the local context as a projection and optimization parameter in demand variability.
Acknowledgements
Universities by releasing their teachers for elaboration of work and Sanitation Company Basico de Agua de Mato Grosso do Sul by the release of water consumption data and number of consumers and the Climate Monitoring Centre and Water Resources of Mato Grosso do South by the release of climate data.
NOTES
*Corresponding author.