New Spiral Curves for Appropriate Transition of Minimum Roadside Clearance on Simple Curves ()
1. Introduction
Sightlines must go through the inside of horizontal curves for drivers to see sufficient lengths of continuous highway sections. Lengths of highway sections are deemed sufficient if they are greater than stopping sight distance. Stopping sight distance is the length of a highway section downstream of drivers that allows the drivers to detect dangerous objects on the roadway then apply brakes to bring the vehicles to rest without hitting the objects. Where there are high objects on the inside of the horizontal curves, such as side-slopes in cut areas, buildings, trees, retaining walls, longitudinal safety barriers, and others, the objects degrade visibility by obstructing sightlines, hence reducing lengths of highway sections that are visible to drivers. If the lengths are reduced to values that are smaller than stopping sight distance there may be safety as well as mobility problems at the curves. To preserve safety and mobility of highways design guidelines require that high objects on the inside of curves be cleared through removal or through locating the objects at sufficient lateral distances from the highways. The lateral distances are technically known as clearance offsets or just offsets. Many design guidelines specify minimum offsets that will guarantee that sections of highways that are visible to drivers are at least equal to stopping sight distance.
For example, one of the design guidelines that specify minimum offsets is the AASHTO’s policy on geometric design of highways and streets, also nicknamed as the Green Book [1] . The guideline has an analytical model for determining the minimum offset as a function of curve radius and stopping sight distance. The model is given by Equation (1) below. Equation (1) was derived with consideration that both drivers and dangerous objects are on a curve such that the distance between the drivers and the objects is equal to stopping sight distance. This consideration makes the equation applicable for driver locations from PC to 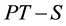 where PC is the point of curvature or beginning of the curve, PT is the point of tangency or end of the curve, and S is stopping sight distance. An offset determined with Equation (1) is simply the middle ordinate from the middle of a curved segment (whose length equals to S) to the midpoint of a sightline. Bisection of sightlines by the offsets is possible only if the offsets are applied within the section from station
where PC is the point of curvature or beginning of the curve, PT is the point of tangency or end of the curve, and S is stopping sight distance. An offset determined with Equation (1) is simply the middle ordinate from the middle of a curved segment (whose length equals to S) to the midpoint of a sightline. Bisection of sightlines by the offsets is possible only if the offsets are applied within the section from station  (corresponding to driver location at PC) to station
(corresponding to driver location at PC) to station 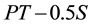 (corresponding to driver location at
(corresponding to driver location at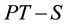 ). Therefore, Equation (1) is well suited for the section from
). Therefore, Equation (1) is well suited for the section from  to
to  and on sites whose curves are longer than stopping sight distance. It is only on those sites where it is geometrically possible for both drivers and objects to be on the curve. Equation (1) is geometrically intuitive and does not need any type of validation.
and on sites whose curves are longer than stopping sight distance. It is only on those sites where it is geometrically possible for both drivers and objects to be on the curve. Equation (1) is geometrically intuitive and does not need any type of validation.
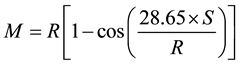 (1)
(1)
where
M is the minimum offset measured from driver path;
R is the radius of curved driver path;
S is the stopping sight distance;
Applying offsets determined with Equation (1) on tangent sections or curved sections near PC or near PT may result in unnecessary extra clearance. Extra clearance may have economic implications like additional earthwork costs on sites where highways pass through cut zones. To avoid the unnecessary costs how should clearance be transitioned from tangent sections where clearance is not necessary to middle sections of curves where clearance is required? The Green Book suggests two methods that may be used for determining transition offsets. The first is the graphical method in which offsets are manually measured on plans. The method consists of drawing chords at intervals such that each chord intersects a segment of driver path that has length equal to stopping sight distance. Figure 1 illustrates the graphical method. The dashed lines in the figure are a representation of a few chords but in practice an interval of 30 ft or 50 ft is adequate. These chords are sightlines from objects that are located a distance equal to stopping sight distance downstream of driver eyes.
After the chords are drawn, a curve that is tangential to all chords is drawn. This curve is a clearance envelope and it is the boundary that marks the roadside area that accommodates sightlines. All high roadside objects may be on the inside of the clearance envelope but not in the area that accommodates the sightlines. To obtain clearance offsets a designer measures lengths of normal ordinates from driver path to the clearance envelope. Lines AB and CD in Figure 1 are examples of offsets at stations A and C, respectively.
Offsets that are measured on plans are laid out in the field to set out the clearance envelope. Offsets that are measured between station 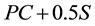 and
and  are the same with values equal to those determined with
are the same with values equal to those determined with
![]()
Figure 1. Graphical method for determining minimum offsets.
Equation (1). These offsets imply that the middle part of the envelope is a circular arc of radius R-M. For sections upstream of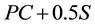 , offsets increase gradually from 0 at
, offsets increase gradually from 0 at 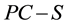 to the value given by Equation (1) at station
to the value given by Equation (1) at station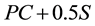 . The gradual increase in offsets implies gradual decrease of radius of the envelope from infinity at
. The gradual increase in offsets implies gradual decrease of radius of the envelope from infinity at 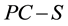 to the value of R-M at station
to the value of R-M at station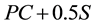 . This gradual decrease of radius hence gradual increase of offsets is perhaps the reason Olson et al. [2] called the portion of the envelope a transition curve for lateral clearance. However, Olson et al. did not derive mathematical representation of the transition curve. There is a possibility that some practitioners and researchers may use equations for the known Euler’s transition or spiral curve as an analytical method for determining transition offsets. They may do that to avoid the graphical procedure due to its time consumption and tedium. An example is the work by Ameri et al. [3] who analyzed roadside clearance with the Euler’s spiral as the clearance envelope.
. This gradual decrease of radius hence gradual increase of offsets is perhaps the reason Olson et al. [2] called the portion of the envelope a transition curve for lateral clearance. However, Olson et al. did not derive mathematical representation of the transition curve. There is a possibility that some practitioners and researchers may use equations for the known Euler’s transition or spiral curve as an analytical method for determining transition offsets. They may do that to avoid the graphical procedure due to its time consumption and tedium. An example is the work by Ameri et al. [3] who analyzed roadside clearance with the Euler’s spiral as the clearance envelope.
The second method suggested in the Green Book is the computational method such as that conducted by Raymond [4] . Raymond developed charts that related offset ratios [fractions of M in Equation (1)] to location. The offset ratios were determined computationally but no mathematical equations used in the computation process were reported. The paper mentioned that the computational process was a numerical form of the graphical method. I have tested the charts and found them to work accurately. However, the charts are suitable for sites with spiraled horizontal curves and for sites with simple curves that are longer than stopping sight distance.
Glennon [5] developed a design chart of offset ratios similar to that of Raymond [4] using the graphical method. The chart is also for long curves. Olson et al. [2] developed a straightforward quadratic relationship between offsets and location for long curves. Probably, this quadratic relationship was proposed only as a rough approximation since most offsets determined with it deviated from those determined with Raymond’s and Glennon’s charts.
A number of studies, including that by Olson et al. [2] , Cleveland et al. [6] , and Waissi and Cleveland [7] , developed relationships between available sight distance (Sav) and an offset to a single roadside obstacle. Easa [8] developed relationships between Sav and an offset to a single obstacle but also demonstrated how the model could be applied to multiple obstacles. Hassan et al. [9] developed models that determined Sav given offsets to continuous obstacles. Further studies were conducted to determine Sav, mostly using methods that subdivided a highway and its surroundings into small geometric elements [10] - [17] . All these models are for evaluating whether or not the determined Sav is greater than design sight distance given offsets to obstructions. In the event Sav is less than design sight distance either an iterative process of applying trial offsets and checking with the models should be conducted or needed is another model for straightforwardly determining minimum clearance offsets that will guarantee that available sight distance is at least equal to design sight distance.
This study has the following objectives.
1. To derive mathematical equations for the roadside clearance envelope.
2. To use the envelope equations to derive equations for transitioning minimum clearance offsets from tangent sections to middle sections of highway curves.
3. To validate the model using design offset data.
4. To examine suitability of the Euler’s spiral curve for analytically determining transition offsets for roadside clearance.
5. To compare the new analytical offsets with offsets determined using models proposed in past studies.
6. To develop a design chart for practitioners.
The analytical model to be developed is for isolated simple curves. Isolated simple curves are those that are separated from other curves by straight sections whose lengths are at least equal to design sight distance. Simple curves are the focus in this paper because they are popular. Even when reverse curves are used, the need for sufficient length for reverse tangents for purposes of transitioning and reversing superelevation results in the reverse tangents having lengths that are near the length of design sight distance. Such lengths of reverse tangents result in the component curves being almost isolated or fully isolated. Agencies that use spirals for transitioning turning on horizontal curves may find related clearance offsets in another work [18] .
2. Model Development
This section presents derivation of mathematical equations for the roadside clearance envelope. The derivation considers the highway section from station  to
to ![]() since this section is where a horizontal curve has impact on roadside visibility as seen in Figure 1 above. The equations so derived are then used to derive equations for offsets whereby offsets are defined as normal ordinates from driver path to the envelope. Derivation is conducted for sites with long curves (i.e. those whose lengths are greater than stopping sight distance) then for sites with short curves. Sites with long curves are considered as case 1 and the latter are case 2.
since this section is where a horizontal curve has impact on roadside visibility as seen in Figure 1 above. The equations so derived are then used to derive equations for offsets whereby offsets are defined as normal ordinates from driver path to the envelope. Derivation is conducted for sites with long curves (i.e. those whose lengths are greater than stopping sight distance) then for sites with short curves. Sites with long curves are considered as case 1 and the latter are case 2.
2.1. Case 1: Long Curves
For sites with curves that are longer than stopping sight distance there are three sub-cases to consider in deriving envelope equations. The first sub-case is when a driver is on the approach tangent and a dangerous object is on the curve. The second sub-case is when the driver and the dangerous object are both on the curve. The third sub-case is when the driver is on the curve and the object is on the receding tangent. In all three sub-cases derivation considers that separation between the driver and the object is equal to stopping sight distance. In other words, the derivation considers that the roadside is minimally cleared such that lengths of highway sections drivers can see are only equal to stopping sight distance. This consideration assures that resulting offsets are minimum values for providing stopping sight distance. Provision of offsets greater than these minimum values will assure that the length of highway drivers can see is greater than stopping sight distance. Below is the derivation of equations of the clearance envelope starting with the first sub-case.
2.1.1. Case 1(a): Driver on the Approach Tangent and Object on the Curve
Quick observation of Figure 1 presented earlier reveals that the distance from driver eyes to the location where a sightline touches the clearance envelope tangentially increases as the driver moves from station ![]() to PC. This relationship is illustrated in Figure 2(a) below. In Figure 2(a), line 2-2 is longer than line 1-1, line 3-3 is longer than line 2-2, and so on. Therefore, the equation of the envelope is derived such that the tangent length of the sightline (such as 1-1, 2-2, 3-3, etc.) is a function of driver location measured from station
to PC. This relationship is illustrated in Figure 2(a) below. In Figure 2(a), line 2-2 is longer than line 1-1, line 3-3 is longer than line 2-2, and so on. Therefore, the equation of the envelope is derived such that the tangent length of the sightline (such as 1-1, 2-2, 3-3, etc.) is a function of driver location measured from station![]() . To derive the equation, first consider Figure 2(b).
. To derive the equation, first consider Figure 2(b).
Figure 2(b) presents a portion of a horizontal alignment of driver path along with its clearance envelope. Point A is at station ![]() and is the origin of an x-y coordinate system with axes positive in the direction of their arrows. The y-axis is positive on the inside of the curve consistent with signs of offsets. Point B is an arbitrary driver location at distance d downstream of
and is the origin of an x-y coordinate system with axes positive in the direction of their arrows. The y-axis is positive on the inside of the curve consistent with signs of offsets. Point B is an arbitrary driver location at distance d downstream of![]() . Coordinates of point B are
. Coordinates of point B are ![]() whereby subscript d to x and y stands for driver location.
whereby subscript d to x and y stands for driver location.
Point ![]() in Figure 2(b) is the position of an object that is S downstream of the driver or distance d downstream of PC. The subscript o to x and y coordinates stands for object location. Sightline BC touches the clearance envelope tangentially at point D with coordinates
in Figure 2(b) is the position of an object that is S downstream of the driver or distance d downstream of PC. The subscript o to x and y coordinates stands for object location. Sightline BC touches the clearance envelope tangentially at point D with coordinates![]() . Line BD is the horizontal length of the sightline from the driver to the point the sightline touches the envelope tangentially. This length is named as the horizontal tangent length TH. To formulate the relationship between TH and d it is hypothesized that TH is linearly proportional to d within the domain
. Line BD is the horizontal length of the sightline from the driver to the point the sightline touches the envelope tangentially. This length is named as the horizontal tangent length TH. To formulate the relationship between TH and d it is hypothesized that TH is linearly proportional to d within the domain![]() . Equation (2) presents the relationship.
. Equation (2) presents the relationship.
![]() (2)
(2)
where
TH is the tangent length of a sightline;
![]()
Figure 2. Relationship between driver location and length of sightline. (a) Sightline tangent length as a function of driver location; (b) Location of driver, object, and sightline tangential point.
d is the driver location downstream of![]() ;
;
C1 is the constant of proportionality.
The constant of proportionality in Equation (2) is determined using known values of d and TH. When a driver is at PC the value of d is S and the value of TH is half the length of the sightline. TH is half the length of the sightline because the clearance offset presented in Equation (1) earlier applies there and the offset bisects the sightline. Equation (3) is for TH as half the length of the sightline when the driver is at PC.
![]() (3)
(3)
where
TM is the value of TH corresponding to M in Equation (1);
β is the angle subtended by a circular arc with length d;
![]() in radians, since
in radians, since ![]() when the driver is at PC;
when the driver is at PC;
![]() in degrees.
in degrees.
Inserting ![]() and
and ![]() in Equation (2) then rearranging, the value of the constant of proportionality is obtained as presented by Equation (4).
in Equation (2) then rearranging, the value of the constant of proportionality is obtained as presented by Equation (4).
![]() (4)
(4)
To complete mathematical representation of the clearance envelope in this sub-case, Equation (2) is complimented by angle θ at which a sightline deflects from the x-axis (i.e. the approach tangent). The general equation for the angle is obtained from coordinates of locations of the driver ![]() and the object
and the object ![]() as shown in Equation (5).
as shown in Equation (5).
![]() (5)
(5)
where
θ is the angle at which a sightline deflects from the approach tangent;
![]() is the x coordinate of a driver,
is the x coordinate of a driver,![]() ;
;
![]() is the y coordinate of a driver,
is the y coordinate of a driver,![]() ;
;
![]() is the x coordinate of an object,
is the x coordinate of an object,![]() ;
;
![]() is the y coordinate of an object,
is the y coordinate of an object,![]() ;
;
β is the angle subtended by a circular arc with length d;
![]() in radians,
in radians, ![]() in degrees.
in degrees.
Equation (6) gives approximate values of θ for curves with radii that are at least greater than design sight distance.
![]() (6)
(6)
where
![]() is the value of θ when a driver is at PC, i.e.
is the value of θ when a driver is at PC, i.e.![]() ;
;
![]() in radians or;
in radians or;
![]() in degrees;
in degrees;
Equations (2) and (5 or 6) are for the part of the envelope between station ![]() and station
and station![]() . The radius of this part of the envelope decreases gradually from infinity at station
. The radius of this part of the envelope decreases gradually from infinity at station ![]() to the minimum of R-M at
to the minimum of R-M at![]() . This gradual decrease in radius makes this part of the envelope a type of spiral. The two variables in Equation (2) are related to two geometric features of the spiral in that driver location d is the first or long tangent and TH is the second or short tangent. The first and second tangents will be denoted as T1 and T2, respectively, later in this paper when this new spiral is compared with the Euler’s spiral.
. This gradual decrease in radius makes this part of the envelope a type of spiral. The two variables in Equation (2) are related to two geometric features of the spiral in that driver location d is the first or long tangent and TH is the second or short tangent. The first and second tangents will be denoted as T1 and T2, respectively, later in this paper when this new spiral is compared with the Euler’s spiral.
2.1.2. Case 1(b): Both Driver and Object Are on the Curve
For a driver and an object to be both on the curve the domain is such that![]() . In this case, the distance from driver eyes to the point where a sightline touches the clearance envelope tangentially is constant. This distance equals half the length of a sightline. Equation (7) is for the sightline tangent as was presented in Equation (3) for a driver at PC.
. In this case, the distance from driver eyes to the point where a sightline touches the clearance envelope tangentially is constant. This distance equals half the length of a sightline. Equation (7) is for the sightline tangent as was presented in Equation (3) for a driver at PC.
![]() (7)
(7)
where
TM is the value of TH corresponding to M in Equation (1);
The angle at which the sightline deflects from the approach tangent increases linearly with the driver location after PC. Equation (8) is for the deflection angle in radians.
![]() (8)
(8)
2.1.3. Case 1(c): Driver on the Curve and Object on the Receding Tangent
The part of the clearance envelope for this sub-case is a spiral such that clearance offsets decrease from values given by Equation (1) at station ![]() to zero at
to zero at![]() . This spiral is simply the image of that between station
. This spiral is simply the image of that between station ![]() and
and ![]() in case 1(a). Therefore, it is taken that the length of the sightline from the object back to the point the sightline touches the envelope tangentially decreases linearly with decrease in object location measured from
in case 1(a). Therefore, it is taken that the length of the sightline from the object back to the point the sightline touches the envelope tangentially decreases linearly with decrease in object location measured from![]() . This decrease in the distance between the tangential point and the object implies that there is linear increase in the distance between the tangential point and the driver. Equation (9) presents the linear relationship with
. This decrease in the distance between the tangential point and the object implies that there is linear increase in the distance between the tangential point and the driver. Equation (9) presents the linear relationship with ![]() as the domain. In the equation TM is the value of TH obtained from Equation (7) above which enters Equation (9) as the initial value of TH when the driver is at
as the domain. In the equation TM is the value of TH obtained from Equation (7) above which enters Equation (9) as the initial value of TH when the driver is at ![]() (i.e.
(i.e. ![]() where L is the length of the curve). The coefficient C2 is obtained by inserting in Equation (9) values of d and TH that are known. When the driver is at PT,
where L is the length of the curve). The coefficient C2 is obtained by inserting in Equation (9) values of d and TH that are known. When the driver is at PT, ![]() , and the object is at
, and the object is at![]() ,
,![]() .
.
![]() (9)
(9)
where
C2 is a constant given by![]() .
.
The angle at which the sightline tangent deflects from the x-axis is determined using the triangle formed by the highway tangents and the sightline prolonged to intersect the two tangents. From the triangle the angle at which the sightline deflects from the approach tangent is the difference between the deflection angle of the horizontal curve and the angle at which the sightline deflects from the receding tangent. The angle at which the sightline deflects from the receding tangent is approximately proportional to the square of the distance from the object to station ![]() similar to Equation (6) for case 1(a). Equation (10) is for θ in this sub-case.
similar to Equation (6) for case 1(a). Equation (10) is for θ in this sub-case.
![]() (10)
(10)
where
∆ is the deflection angle of the horizontal curve;
![]() is the distance from the object to
is the distance from the object to![]() .
.
C3 is a constant given by![]() .
.
The equations of the clearance envelope in case 1 may be written as one equation with three regimes both for the sightline tangent length and for the angle at which the sightline deflects from the approach tangent. Equations (11) and (12) present the equations.
![]() (11)
(11)
![]() (12)
(12)
2.2. Case 2: Short Curves
Short curves are horizontal curves whose lengths are shorter than stopping sight distance. Envelope equations for this case are closely related to the equations for long curves except when a driver is on the approach tangent and an object is on the receding tangent.
2.2.1. Case 2(a): Driver on the Approach Tangent and Object on the Curve
This case is the same as case 1(a) but the driver does not go all the way to PC since L < S. As the driver location d exceeds L the object location changes from the curve to the receding tangent. The domain of this sub-case is thus![]() . Equation (13) is for case 2(a).
. Equation (13) is for case 2(a).
![]() (13)
(13)
The angle of deflection of the sightline from the approach tangent is also the same as that for case 1(a).
![]() (14)
(14)
2.2.2. Case 2(b): Driver on the Approach Tangent and Object on the Receding Tangent
The equation for this sub-case is given by Equation (15) below. The domain of the equation is![]() . The intercept of the equation is obtained from the maximum value of TH in Equation (13). The maximum value of TH in Equation (13) is obtained when a driver is at distance L downstream of PC-S. To obtain the value of the constant C4 the location of driver corresponding to maximum offset is used. That diver location is such that the sightline deflects at an angle of 0.5∆ from the approach tangent. The value of d corresponding to that location is
. The intercept of the equation is obtained from the maximum value of TH in Equation (13). The maximum value of TH in Equation (13) is obtained when a driver is at distance L downstream of PC-S. To obtain the value of the constant C4 the location of driver corresponding to maximum offset is used. That diver location is such that the sightline deflects at an angle of 0.5∆ from the approach tangent. The value of d corresponding to that location is ![]() and the value of TH is TM where TM is half the length of the sightline as shown in Figure 3. Insertion of
and the value of TH is TM where TM is half the length of the sightline as shown in Figure 3. Insertion of ![]() and TM in Equation (15) gives the value of the constant C4.
and TM in Equation (15) gives the value of the constant C4.
![]() (15)
(15)
where
C4 is a constant given by![]() ;
;
![]() in Figure 3;
in Figure 3;
![]() ;
;
The corresponding deflection angle increases linearly with increase in driver location after![]() . The equation for the deflection angle is given by Equation (16). The domain of the equation is also
. The equation for the deflection angle is given by Equation (16). The domain of the equation is also![]() . The first term of the equation is the maximum value of Equation (14) when
. The first term of the equation is the maximum value of Equation (14) when ![]() in the previous sub-case and hence the initial value of Equation (16). It is also known that when
in the previous sub-case and hence the initial value of Equation (16). It is also known that when ![]() the angle is 0.5∆. These two values are used to determine the rate of change of the deflection angle per unit change in driver location after
the angle is 0.5∆. These two values are used to determine the rate of change of the deflection angle per unit change in driver location after![]() . The rate is presented in the square brackets in Equation (16)
. The rate is presented in the square brackets in Equation (16)
![]() (16)
(16)
![]()
Figure 3. Tangent to envelope at maximum offset for the case L < S.
2.2.3. Case 2(c): Driver on the Curve and Object on the Receding Tangent
This part of the envelope curve is the mirror image of that in case 2(a). Equation (17) presents the relationship for the case. The domain of the equation is![]() . The first two terms of the equation sum to the minimum value of TH when
. The first two terms of the equation sum to the minimum value of TH when ![]() (i.e. the driver is at PC). The two terms were obtained as maximum value of TH in the previous case as per Equation (15). The coefficient C5 is calculated by inserting the upper limit of the domain of Equation (17). When a driver is at PT,
(i.e. the driver is at PC). The two terms were obtained as maximum value of TH in the previous case as per Equation (15). The coefficient C5 is calculated by inserting the upper limit of the domain of Equation (17). When a driver is at PT, ![]() and the object is at
and the object is at ![]() hence
hence![]() .
.
![]() (17)
(17)
where
C5 is a constant given by![]() .
.
The angle of deflection of a sightline from the approach tangent is given by Equation (18). Equation (18) was obtained in the similar way that of case 1(c) was.
![]() (18)
(18)
Equations (19) and (20) group all the sub-cases for the sightline tangent length and deflection angle in case 2, respectively.
![]() (19)
(19)
![]() (20)
(20)
where
C6 is a constant given by![]() .
.
2.3. Equations for Offsets
Coordinates of points where sightlines touch the envelope tangentially are used to determine clearance offsets. Using Equations (11) and (12) for long curves and Equations (19) and (20) for short curves, equations for coordinates of the tangential points are obtained. Equations (21) and (22) are for coordinates of the tangential points. These equations are a parametric way of representing the clearance envelope.
![]() (21)
(21)
![]() (22)
(22)
where
![]() is the x coordinate of driver location;
is the x coordinate of driver location;
![]() is the y coordinate of driver location.
is the y coordinate of driver location.
Offsets for the section between ![]() and PC are simply the y-coordinates of the envelope as per Equation (22) and as shown in Figure 4(a) at point B.
and PC are simply the y-coordinates of the envelope as per Equation (22) and as shown in Figure 4(a) at point B.
![]() (23)
(23)
where
m is an offset from driver path to the envelope.
The equation for offsets from the circular part of the driver path (like point C in Figure 4(a)) is derived below.
![]() (24)
(24)
![]()
Figure 4. Relationship between offsets and coordinates of the envelope. (a) Horizontal offsets from the approach tangent and curve; (b) Horizontal offsets from the receding tangent.
But
![]() (25)
(25)
Inserting (25) in (24) yields Equation (26).
![]() (26)
(26)
Equation (26) works for all stations between PC and PT inclusive. This equation yields values of offsets equal to those determined with Equation (1) for the middle section of long curves from ![]() to
to![]() .
.
An offset from the second highway tangent (like point G in Figure 4(b)) is given by Equation (27) and (28).
![]() (27)
(27)
![]() (28)
(28)
Grouping Equations (23), (26), and (28), yields Equation (29) for offsets from ![]() to
to![]() . This equation is the analytical model of offsets that this paper seeks to present.
. This equation is the analytical model of offsets that this paper seeks to present.
![]() (29)
(29)
where
![]() is the offset;
is the offset;
![]() is the central angle as shown in Figure 4(b).
is the central angle as shown in Figure 4(b).
X is the station of the offset.
3. Verification of the Offset Model
Verification of the analytical model for clearance offsets requires comparing calculated offsets with design offsets. Design offsets are determined with the graphical method presented earlier. The reason for considering the graphical offsets as design offsets is that the graphical method orients sightlines on plans the same way the sightlines are oriented in the field. This mimic of sightline orientation renders the graphical method geometrically sound and hence accurate. It is geometric soundness and accuracy that got it recommended by the AASHTO’s Green Book and accepted by researchers, and practitioners. In fact, Raymond [4] developed offset charts from the graphical method indirectly through numericizing it while Glennon [5] developed offset charts using the graphical method directly. Moreover, some commercial software do use the graphical method to check sight distance requirements. Researchers who have written on the subject of roadside clearance have not criticized the graphical method for no soundness or inaccuracy but for time consumption and tedium. In the absence of analytical models suggested in the past it is the offsets produced with the graphical method in the design room that would be used reliably in the field. Offsets measured in the field would still equal to graphical offsets since it is the graphical method in the first place that was used to develop the offsets before they were laid out in the field. Being good for implementation in the field, the graphical offsets are good for model verification.
Figure 5 presents two sets of offset data. Figure 5(a) presents the first set which is for a site with a long horizontal curve i.e. L ≥ S. Offsets in Figure 5(a) have been determined with the analytical model as well as with the graphical method for a 50 mph (S = 425 ft.) highway with a curve 650 ft. long and a radius 650 ft. long. It is apparent that the two models produce the same values of offsets. Agreement of the analytical offsets with the graphical offsets verifies geometric soundness of the derived equations for the clearance envelope and offsets. That is, the linear relationship between TH and d that is hypothesized in this paper is accurate for practical purposes and nonlinearity that may be in the unknown exact relationship between TH and d is negligibly small.
The second set of offsets is presented by Figure 5(b) for a site with a short horizontal curve i.e. L < S. The figure has two offset data for a 50 mph highway with a curve 250 ft. long and a radius 650 ft. long. The analytical offsets concur with offsets that are determined with the graphical method. Agreement of the analytical offsets with those determined with the graphical method validates the analytical model for the case L < S.
4. Suitability of the Euler’s Spiral
The portion of the clearance envelope between station ![]() and
and ![]() has radius gradually decreasing from infinity at
has radius gradually decreasing from infinity at ![]() to R-M at
to R-M at![]() . This property of gradual decrease in radius makes that part of the envelope a kind of a spiral. Is this spiral the Euler’s spiral that is used for transitioning turning at horizontal curves? Relevance of this question stems out from the fact that some practitioners and researchers may opt for the Euler’s spiral as an analytical method for transitioning clearance since mathematical representation of the spiral is already known. This section examines suitability of the spiral by comparing its offsets with offsets determined using the spiral derived and validated in this paper.
. This property of gradual decrease in radius makes that part of the envelope a kind of a spiral. Is this spiral the Euler’s spiral that is used for transitioning turning at horizontal curves? Relevance of this question stems out from the fact that some practitioners and researchers may opt for the Euler’s spiral as an analytical method for transitioning clearance since mathematical representation of the spiral is already known. This section examines suitability of the spiral by comparing its offsets with offsets determined using the spiral derived and validated in this paper.
![]()
Figure 5. Comparison between analytical and graphical offsets. (a) Agreement of analytical and graphical offsets for L ≥ S. (b) Agreement of analytical and graphical offsets for L < S.
Consider the offset at station ![]() on the 50 mph (S = 425 ft) highway with a 650 ft. radius and a 650 ft curve. At station
on the 50 mph (S = 425 ft) highway with a 650 ft. radius and a 650 ft curve. At station![]() , the clearance offset is that determined with the model in the Green Book i.e. Equation (1). That offset is 34.43 ft as shown below.
, the clearance offset is that determined with the model in the Green Book i.e. Equation (1). That offset is 34.43 ft as shown below.
![]() (30a)
(30a)
![]() (30b)
(30b)
The radius of the envelope at station ![]() is determined by subtracting the offset from the radius of the driver path.
is determined by subtracting the offset from the radius of the driver path.
![]() (31a)
(31a)
![]() (31b)
(31b)
where
Re is the radius of the envelope curve.
The angle at which the sightline deflects from the x-axis is determined based on the driver location at PC.
![]() (32a)
(32a)
![]() (32b)
(32b)
The length of the sightline from the driver at PC to the envelope at ![]() is half length of the whole sightline.
is half length of the whole sightline.
![]() (33)
(33)
The x and y coordinates on the envelope at station ![]() are calculated using Equations (21) and (22) with the deflection angle and sightline tangent length calculated using Equation (32) and (33), respectively.
are calculated using Equations (21) and (22) with the deflection angle and sightline tangent length calculated using Equation (32) and (33), respectively.
![]() (34a)
(34a)
![]() (34b)
(34b)
![]() (35a)
(35a)
![]() (35b)
(35b)
For the Euler’s spiral to be suitable, it must have the same y-coordinate of 67.04 ft at station![]() . The length of the Euler’s spiral that has the y-coordinate of 67.04 ft is determined using Equation (36).
. The length of the Euler’s spiral that has the y-coordinate of 67.04 ft is determined using Equation (36).
![]() (36a)
(36a)
![]() (36b)
(36b)
where
Ys is the y-coordinate of the end of the spiral;
Ls is the maximum length of the spiral.
The length of the spiral so obtained is shorter than the expected x-coordinate at ![]() as per Equation (34). Being shorter implies that the Euler’s spiral does not start at PC-S. Table 1 summarizes geometric features of the spiral and compares with features of the new or proposed spiral.
as per Equation (34). Being shorter implies that the Euler’s spiral does not start at PC-S. Table 1 summarizes geometric features of the spiral and compares with features of the new or proposed spiral.
Table 1 shows that the Euler’s spiral differs from the proposed spiral starting with definitions. The table shows that the Euler’s spiral is shorter, with shorter tangents, with larger spiral angle, than the proposed spiral. The Euler’s spiral is hence sharper than the proposed spiral. The combination of shorter tangents and larger spiral angle implies that the point of intersection of tangents of the Euler’s spiral is not at station PC, while in the graphical method and with the new spiral the tangents intersect at PC. However, the ultimate test of the Euler’s spiral lies in the examination of clearance offsets.
Figure 6(a) presents offset curves determined with the Euler’s spiral, past models, as well as the offset curve determined with the proposed spiral for the 50mph highway with radius of 650 ft and a horizontal curve that is longer than stopping sight distance. The offsets are for the section between station ![]() and
and![]() .
.
In Figure 6(a), it is observed that offsets determined with the Euler’s spiral are consistently smaller than offsets determined with past models and with the proposed spiral except at station![]() . Since offsets determined with the proposed spiral were verified in the previous section, being smaller than these offsets, offsets determined with the Euler’s spiral are considered underestimates of required offsets. For example, at PC the offset determined with the Euler’s spiral is 13.6 ft while the offset determined with the proposed spiral and other models is 20.7 ft. Implementing the 13.6 ft offset will reduce available sight distance to 345 ft which is less than the minimum or stopping sight distance of 425 ft. Reduction of available sight distance to that extent has safety as well as mobility consequences. In addition, the offset curve for the Euler’s spiral does not transition smoothly to the minimum offset proposed in the Green Book at
. Since offsets determined with the proposed spiral were verified in the previous section, being smaller than these offsets, offsets determined with the Euler’s spiral are considered underestimates of required offsets. For example, at PC the offset determined with the Euler’s spiral is 13.6 ft while the offset determined with the proposed spiral and other models is 20.7 ft. Implementing the 13.6 ft offset will reduce available sight distance to 345 ft which is less than the minimum or stopping sight distance of 425 ft. Reduction of available sight distance to that extent has safety as well as mobility consequences. In addition, the offset curve for the Euler’s spiral does not transition smoothly to the minimum offset proposed in the Green Book at![]() . This kinky transition at
. This kinky transition at ![]() together with underestimation of offsets is due to high degree of sharpness of the Euler’s spiral.
together with underestimation of offsets is due to high degree of sharpness of the Euler’s spiral.
In Figure 6(a), it is also observed that offsets determined with the proposed spiral are in agreement with offsets determined with Raymond’s charts [4] . Since Raymond did not report mathematical background of the charts, it is claimed that the equations developed in this paper are representatives of the equations that were used to produce the Raymond’s charts for simple curves. Offsets determined with the model by Glennon [5] slightly
![]()
Table 1. Comparison between Euler’s and proposed spirals.
deviate from the proposed model may be due to minor errors in developing or reading the offsets. Offsets determined with the quadratic model by Olson et al. [2] are in disagreement with offsets by Raymond, Glennon, and the proposed spiral except at three locations: at![]() , PC, and
, PC, and![]() . The quadratic model overestimates offsets on tangent sections where clearance is already provided by lanes and shoulders but underestimates offsets on the curved section where clearance is needed most.
. The quadratic model overestimates offsets on tangent sections where clearance is already provided by lanes and shoulders but underestimates offsets on the curved section where clearance is needed most.
Figure 6(b) is for offsets on the 50 mph highway with 650 ft radius but with 250 ft horizontal curve. It is observed that the Euler’s spiral consistently underestimates offsets even on short curves.
5. Design Chart
In developing charts that designers can use to determine offsets, used is the property that highway curves with the same length L, radius R, and stopping sight distance S have the same offset m at similar location X. These five elements are cut down to four if they are expressed as ratios. That is, highway curves having the same L/S and R/S ratios have the same offset ratio m/MAASHTO at the same location with location ratio X/(2S + L). MAASHTO is the offset determined using the model in the Green Book i.e. Equation (1).
Figure 7 presents one design chart for both cases L ≥ S and L < S. The horizontal axis is for location ratio X/(2S + L) and the vertical axis is for offset ratio m/MAASHTO. The chart is for various L/S ratios and R/S ≥ 1.5.
The R/S ratio is an indicator of how flat a curve is relative to sight distance. Offsets are insensitive to R/S ratios that are greater than 1.5. Figure 8(a) presents m/MAASHTO ratios at PC or PT as a function of R/S ratio. It is evident that for a given L/S ratio, offsets ratios are approximately equal for R/S > 1.5. For R/S < 1.5, offset ratios increase at increasing rates with decrease in R/S ratio. PC or PT have been chosen for presentation of the relationship between offset ratios and R/S ratio since at these points offsets have highest sensitivity to R/S ratio for R/S < 1.5. At other locations, say at PC + 0.5L, offsets are sensitive to R/S ratio for R/S < 1.5 but the sensitivity is low. Figure 8(b) presents the relationship between offset ratios and R/S ratio at PC + 0.5L. It is evident that the offset curves on the left of R/S = 1.5 do not rise as high above values on the right of R/S = 1.5 as offset curves in Figure 8(a) do. Although offsets are sensitive to R/S < 1.5, the chart in Figure 7 is still suitable for most highway curves since the recommendation in the Green Book to provide radii above minimum values will
![]()
Figure 6. Comparison between the proposed and Euler’s spirals. (a) Comparison between proposed, Euler’s, and other offset models for L ≥ S; (b) Comparison between proposed and Euler’s offsets for L < S.
result in the radii that are greater than design sight distances. For few sites with R/S < 1.5 designers may use Equation (5), (11) and (19) to obtain exact offsets. These equations are easily programmable in Excel but the author of this paper may provide an already programed Excel sheet upon request.
As an example of how to use Figure 7, consider a 60 mph 4-lane divided highway. The centerline of the inside lane has a radius of 1500 ft and a length of 685 ft. The minimum clearance offset at station PT is calculated as follows.
Stopping sight distance for 60 mph is S = 570 ft [1] .
R/S ratio is 1500/570 = 2.63 > 1.5, OK.
The offset determined using Equation (1) is:
![]() .
.
![]()
PT is located 570 ft + 685 ft = 1255 ft from![]() .
.
The location ratio is![]() .
.
The L/S ratio is![]() , use the line for L/S = 1.2.
, use the line for L/S = 1.2.
Using the two ratios, m/MAASHTO is 0.6.
![]()
Figure 8. Sensitivity analysis of the design chart. (a) Sensitivity of offset ratio to R/S ratio at PC or PT; (b) Sensitivity of offset ratio to R/S ratio at PC + 0.5L.
The minimum offset at PT is ![]()
Applying the 18 ft offset at PT will provided the sight distance of 570 ft. Any clearance that is greater than 18 ft, say the 30 ft determined using the model in the Green Book, will provide sight distance that is greater than 570 ft. However, the extra 12 ft of clearance could mean extra earthwork cost if the curve was in a cut zone.
6. Conclusions
Sight distance is an element of design of highways. To ensure provision of sufficient sight distance on horizontal curves design guidelines require that the area on the inside of the curves be cleared of sight obstructions. The boundary of the minimum roadside area to clear is known as the clearance envelope. The portion of the clearance envelope near station PC is a transition curve (or spiral) that gradually transitions clearance from straight sections of highways where clearance is unnecessary to middle sections of horizontal curves where clearance is a requirement. Also, the portion of the envelope near PT is a spiral. However, there has been no mathematical representation of the spirals for long time. Absence of mathematical representation of the spirals may tempt practitioners and researchers to use the already known Euler’s spiral as an analytical means of transitioning clearance if they want to avoid the tedious but accurate graphical method. Temptation to use the Euler’s spiral may be coming from naming of the two parts of the envelope as spirals even though suitability of the Euler’s spiral for transitioning clearance is unknown. To differentiate between the two parts of the envelope and the Euler’s spiral the envelope parts may be called roadside spirals, clearance spirals, envelope spirals, or any other short names that may be deemed suitable.
This paper presents derivation of mathematical equations for the clearance envelope on the inside of long and short horizontal curves. The equations are then used for derivation of equations of transition offsets. The equations of the offsets are verified using offsets determined with the graphical method.
An examination of the use of the Euler’s spiral for roadside clearance has been conducted. It has been found that the Euler’s spiral is shorter and hence sharper than the new roadside spirals derived in this paper. Consequently, sharpness of the Euler’s spiral makes offsets determined with it smaller than required values. The Euler’s spiral is therefore unsuitable for transitioning clearance.
Finally, the paper presents a design chart that has been developed using derived offset equations. This chart simplifies determination of offsets even when practitioners are on site and without computers. However, the mathematical equations for the envelope and offsets are still a general solution that practitioners may use through coding the equations in computers. Use of either the design chart or the offset equations will help agencies save money that would otherwise be spent for unnecessarily over-clearing the roadside areas near beginnings and ends of horizontal curves.