1. Introduction
The Ayurvedas depicted that the alcohol behave as a medicine if it is taken for the purpose of meditation otherwise it behave as a poison if it is taken in addiction manner for the humans. The liquor habits reflect person’s social status and cultural prestige. It is observed that transmission of liquoring spreads frequently these days due to availability of the liquor in the market. There is a similarity between spread of infectious disease and liquor habits. In other words, liquor habit can be treated as a virus which transmits among the compartments by social pressure like parties with friends, peers and executive meetings.
In this paper, we analyze quantitative model of a liquor habit transmission in a population similar to SEIR- model. The notations are described in Section 2. The mathematical model and basic reproduction number are formulated in Section 3. The local and global stability are derived in Sections 3.2.1 and 3.2.2 respectively. Numerical simulations are illustrated in Section 4 using State-Space model. Discussions and conclusions are given in Section 5.
2. Notations
The model is derived using following notations.
3. Mathematical Model
Anybody in the population is susceptible to liquor. In general, one starts taking pegs and increases it gradually. The consumption of two pegs is considered as a normal which falls in E-compartment. The work stress, financial stress, and many more factors to go for more than two pegs which fall under I-compartment. Certain fraction of population from E- and I-compartments may be removed. It is taken as R-compartment. Thus, it resembles toSEIR-model.
Let us call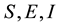 
and R the portion of total population of each class. Now, we make SEIR-model with some assumptions. The portion of liquored person’s who increases liquor habit at a rate proportional to 
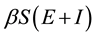with
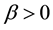. So, the portion of liquored will decrease with the some rate. Here, 
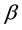is called the effective liquoring rate. The portion of liquor person’s starting liquoring habit with a rate 
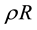(progression rate) with 
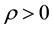and 
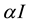with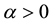
. The portion of excessive liquored with the rate c with
. The portion of removing liquor habit with the rate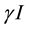 
with 
and 
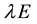with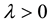
. See the transfer diagram given in Figure 1.
From Figure 1, the model is formulated as following system of differential equations.
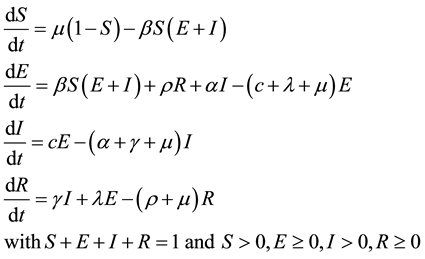(1)
Since, an epidemic model occurs in a short time period, we ignore moving portion of removal from liquor. So, we will analyze the first three equations forming new reduced system
![]()
(2)
Adding all these three equations, we have
![]()
Which gives,![]()
.
Therefore, the feasible region for (2) is
![]()
.
Now, the basic reproduction number ![]()
will be found by using the next generation matrix. It is easy to see that (2) always has a liquor free equilibrium![]()
.
Let![]()
, where dash denotes derivative. So that
![]()
where ![]()
denotes the rate of appearance of new liquored in compartment and ![]()
represents the rate of transfer of liquors, which is given as
![]()
![]()
F and V are ![]()
matrices defined as
![]()
.
So
![]()
where V is non-singular matrix, so that
![]()
(3)
Hence, the basic reproduction number ![]()
is
![]()
= spectral radius of matrix![]()
.
![]()
(4)
Next, we need to discuss equilibrium of the liquor habit system.
3.1. Equilibrium
The liquor free equilibrium is locally asymptotically stable if all the eigenvalues of the matrix have positive real values (Al-Amoudi et al. (2014) [1] ).
Theorem 1 (Johnson (2004) [2] ): Consider the liquor transmission model given by (2) with![]()
. If ![]()
is a liquor free equilibrium of the model, then ![]()
is locally asymptotically stable if![]()
, and unstable if![]()
, where ![]()
is given by (4).
Proof Let![]()
. Since V is a non-singular matrix and F is non-negative,
Thus ![]()
has the Z-sign pattern.
![]()
Û ![]()
isa non-singular matrix.{![]()
is spectral abscissa of j}
Since ![]()
is non-negative, also ![]()
has the Z-sign pattern.
Then, we have ![]()
is a non-singular matrix Û ![]()
is a non-singular matrix.
Finally, since ![]()
is non-negative, all eigenvalues of ![]()
have magnitude less than or equal to![]()
.
Thus, ![]()
is a non-singular matrix Û![]()
.
Hence, ![]()
if and only if![]()
.
Similarly, it follows that ![]()
Û ![]()
is a singular matrix.
Û ![]()
is a singular matrix.
Û![]()
.
Hence, ![]()
if and only if![]()
.
It follows that ![]()
if and only if![]()
.
3.2. Stability of the Equilibrium
3.2.1. Local Stability
The liquor free equilibrium is stable if all the eigenvalues of the Jacobian matrix of the system (1) have negative real parts. For this, the Jacobian of the system (1) at ![]()
takes the form
![]()
Here![]()
.
3.2.2. Global Stability
The liquor free equilibrium is globally stable if![]()
.
![]()
where![]()
.
4. Numerical Simulation
In this section, we perform numerical simulation of the system (1) using with the state-space model.
State-Space Model
State equation ![]()
Output equation ![]()
where u-input, y-output, x-state vector.
The general state-space description for a linear time invariant, continuous time dynamical system is
![]()
where ![]()
are matrices,![]()
. Using this state-space model, we find the solution of the system (1). Taking data as follows:
![]()
in ![]()
![]()
![]()
and ![]()
We carry out the simulation. The results are shown in Figure 2.
5. Discussion and Conclusions
From Figure 2(a), it is observe that 11% of the population from the susceptible compartment start liquoring exponentially in first five weeks. Liquoring habit in the susceptible class is small initially but thereafter it increases exponentially. Figure 2(b) is about those who are taking two or less than two pegs in 10 weeks which shows uniform increase, while 44% of the population is getting liquored in infectious class (Figure 2(c)). It is observed
![]()
Figure 2. (a) Susceptible vs weeks; (b) Expose vs weeks; (c) Infectious vs weeks; (d) Removal vs weeks.
that more than two pegs are taken immediately after 3rd week and increases exponentially. Almost 15% gets chain liquor (those who can’t survive without liquor). The removal compartment (Figure 2(d)), 44% enters either into less than two pegs i.e. E-compartment or into never liquor that is S-compartment.
In this paper, a nonlinear mathematical model for liquor transmission is analysed. The local and global stability of the liquor free equilibrium point are established. It is proved that the free equilibrium is locally asymptotically stable when basic reproduction number ![]()
and global stability of liquor transform![]()
.
This model can be extended by educating youth for non-liquoring via advertisement, rehabilitation centre etc.
Acknowledgements
The first author thanks DST-FIST file # MSI-097 for technical support.