Carbon Black and Multi Wall Carbon Nanotubes Loaded Polyurethane Foam Composite Flexible Thermal Radiator ()
1. Introduction
Flexible thermal radiators (FTRs) are been constructed with textiles manufacturing processes [1]. Several methods have been employed. Weaving or knitting carbon loaded yarns or stainless steel yarns into flexible structures and applying a voltage through these structures is a one approach that has been commonly used [2] [3]. Also putting conductive foam in between two electrodes and passing the current through the foam is practiced widely [4]. Applying a carbon loaded polymer coating or inherently conductive polypyrolle based coating is ano- ther method [3]. In another approach a textiles structure is constructed of carbon based organic polymeric (cotton) yarns or fibres and then it is half burnt by either chemically or flaming [3]. Another method of construction of a flexible heater is by using carbon or stainless steel based short fibres and arranging them by using nonwoven processes [5]. The methods that were discussed above paragraph, the radiation of the heat is in all directions. Therefore not efficient when used in applications where the heat flow direction needed to be controlled such as kidney heating or body warming. During this research the construction of a FTR was carried out to address these limitations. The construction was carried out by using textiles manufacturing methods. This FTR is composed of two layers one contains the powering electrodes and the other the heating element. The electrodes layer is constructed with knitting in the prototypes that were tested but can be constructed with woven or nonwoven as well. The electrodes are constructed in a comb arrangement (Figure 1). The second layer is a heating element that is made by CB loaded foam or MWCNT loaded foam. Both types of prototypes are made for the testing.
The connection between the layers is done by using either by using stitch bonding. The electro-thermal analysis of the FTR is carried by using finite element method. The comparison of the simulation and experimental values are also discussed (Chapter 4). Applications and advantages of FTR are discussed in Chapter 5. The temperature distribution, warm up time to the steady state and power conversion efficiency were measured and presented in the paper.
2. Construction of the FTR
The FTR has two layers, an electrodes layer and a heating layer. FTR is constructed in three steps, constructing electrodes layer, constructing heating layer and connecting them together. The first layer of the FTR is consists of the powering electrodes and which are embedded in electrical insulation material such as polyamide. This layer is constructed with knitting. The powering electrodes were constructed together with the insulating material such that the electrodes and the insulating materials are embedded in the same fabric layer. Silver (Ag) coated polyamide (X static) [6] yarns are used for the electrodes and Nylon (polyamide) yarns are used for the nonconductive sections of this first layer.
The second layer is the thermal radiator and it is constructed by using CB-loaded polyurethane foam or MWCNT loaded polyurethane foam. Both types of foams prepared for the testing. The first and the second layers are joined by stitch bonding. Two groups of FTRs that is CB loaded foams and MWCNT loaded foams are prepared.
2.1. Construction of the Powering Electrodes
The powering electrodes (Figure 2) are arranged in a comb configuration. The comb configuration is used to achieve a uniform heat distribution. The comb electrode structure is constructed by using two intarsia feeders [7]-[9]. Two for electrodes and one for the insulating base on an electronic flatbed knitting machine (Figure 2). Then the silver yarns are fed through these feeders. The insulating base structure is constructed with a polya-
![]()
Figure 1. Flexible thermal radiator (FTR).
![]()
Figure 2. Construction of fabric electrode layer by electronic flat bed knitting.
mide yarn with another separate feeder. Silver coated polyamide 170 dtex yarns and insulating polyamide 220 dtex yarns are used.
When constructing the electrode areas a very closely packed stitches are used. This is to avoid the variation of the resistance of the electrodes during deformation of the FTR. The effect of the open stitches on an electrode is discussed in the reference [10].
2.2. Preparation of CB and MWCNT Loaded Electro Conductive Foam
When selecting suitable conductive foam for the radiating layer thermal stability of the polymer matrix, CB/ MWCNT concentration, type of the polymer matrix, porosity of the foam, thickness of the polymer matrix, and the dimensions of the foam are considered. In order to improve the thermal radiation one side (the side that is exposed to the body) of the foam is formed to a sinusoidal surface (Figure 3). The thickness of the foam is selected such that the radiation is optimized. The filing factor of the CB and the MWCNT plays an important role [11] [12], they are selected optimally. If the concentrations are too high the foam becomes inflexible and the lifetime of the foam is also get reduced. Moreover a significant increase of the resistance with aging is observed. Therefore an optimal CB/ MWCNT concentration is vital for the construction.
2.3. Bonding of the Electrodes Layer and CB/MWCNT Loaded Foam
The third step of the construction is binding of the two layers together by using stitch bonding. The electrodes layer is put on the flat surface of the CB/MWCNT loaded foam and then they are fed to a sewing machine. Insulating yarns are used for the stitches in order to prevent hot spots in the structure and also to improve the duration of the FTR. The stitches are done along the conductive tracks of the comb electrodes (Figure 4). The amplitude of the sinusoidal surface is 5 mm and the pitch is 4 cm (Figure 4). The thickness of a single line of the comb electrode is 2 mm (Figure 4). Also the thickness of the fabric is 1 mm. Figure 4 shows the cross section view of the FTR along a conductive track of a comb line.
3. Electro Thermal Model of the FTR
The FTR consist of two layers comprised of three parts. Namely CB/MWCNT loaded foam and two fabric elec-
trodes. The CB/MWCNT loaded foam is treated as an isotropic and homogeneous continuum. Due to the high loop density of the electrodes, they are assumed as an isotropic homogeneous continuum of 1 mm thickness. Moreover it was also assumed that the conductive materials are purely conductive so that there are no diffusing current components. Also the electrical conductivities of the CB/MWCNT are dependent of the temperature and has nonlinear characteristics [11]. The electrodes have linear temperature dependent electrical conductivities. The physical properties such as densities, specific heat capacities and thermal conductivities are all have temperature dependent nonlinear characteristics for the both CB/MWCNT load foam and the electrodes materials [11] [12]. The 3 parts are shown in the following Figure 5.
The FTR is powered by two diagonal corners of the comb electrodes. The external environment of the FTR is set to be normal environmental conditions. The contact between the electrodes and the heating element is assumed to be a fixed contact. The effect of the insulating parts are neglected.
3.1. Mathematical Model
The model is a classic nonlinear electro-thermal coupled problem [13]-[24]. It can be solved numerically by using various methods and in this paper I used nonlinear finite element analysis method.
The electro thermal transient equation is given by,
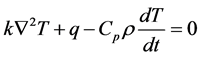 (1)
(1)
where k is the thermal conductivity, T is the temperature, q internal power density, 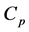 specific heat capacity, t is the time and
specific heat capacity, t is the time and  is the density. T is a function of location and time (T(x, y, z, t)).
is the density. T is a function of location and time (T(x, y, z, t)).
The electro thermal steady state equation is given by,
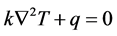 (2)
(2)
where
![]()
The electrical field strength E and electric potential is given by,
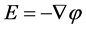 (3)
(3)
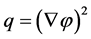 (4)
(4)
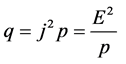 (5)
(5)
where, j is the current density and p is resistivity
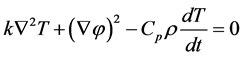 (6)
(6)
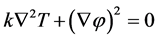 (7)
(7)
The Equation (6) is used for the transient analysis and Equation (7) is used for the steady state analysis. The nonlinear parameters are given as tabulated data with respect to temperature.The meshed FTR is shown in Figure 6.
![]()
Figure 5. Two electrodes and the heating element.
3.2. Simulation Results
The CB load FTR and the MWCNT load FTR are simulated separately. Figures 7(a)-(c) are showing the steady state simulated results with Abaqus.
3.3. Measurement of Temperature
Spatial distribution of the temperature is measured by using a thermocouple. The experimental setup is shown in Figure 8. Figure 9 shows the results obtained from the temperature measurements.
3.4. Transient Thermal Analysis
The transient properties of the FTR are tested and it is observed that it can be modelled by piece wise exponential functions. The rise times and the fall times are calculated by using the empirical exponential equations the results are shown in the Figure 10.
A first order transient behaviour is observed and therefore it can be modelled by using first order exponential equations.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 7. (a) MWCNT FTR(left) and CB FTR (right) Normalized Temperature Distribution; (b) MWCNT FTR(left) and CB FTR (right) Normalized Voltage Distribution; (c) MWCNT FTR(left) and CB FTR (right) CurrentDensity Distribution.
![]()
Figure 9. MWCNT FTR(left) and CB FTR (right) Measured Temperature Profile.
![]()
Figure 10. Transient response of the MWCNT, CB Load FTR.
![]() (8)
(8)
where ![]() is the temperature at a given time t, K is the time constant, Tsteady is the steady state temperature, T0 is the ambient temperature and K is the time constant. K was estimated by using the experimental data.
is the temperature at a given time t, K is the time constant, Tsteady is the steady state temperature, T0 is the ambient temperature and K is the time constant. K was estimated by using the experimental data.
3.5. Discussion of the Results
It was observe that the temperature distribution of MWCNT loaded FTR is more uniform than the CB loaded FTR (Figure 7(a)). MWCNT FTR hotspots are more concentrated than CB loaded FTRs (Figure 7(b)). MWCNT FTR voltage distribution is more uniform than CB loaded FTRs (Figure 7(a)). Transient heating up and cooling times of CB and MWCNT loaded FTRs are observed and MWCNT it was observed that MWCNT has faster time constants both heating and cooling (Figure 10). In addition MWCNT FTR would expected to have better aging performance.
4. Applications
These FTRs are used in heater cloths, aerospace industries and medical applications. In addition they can be used in floor heating and wall heating applications. These FTRs are also constructed by using large-scale textiles manufacturing processes such as weaving, knitting (warp/weft) and nonwoven lamination.