A Synoptic Review on Deriving Bathymetry Information Using Remote Sensing Technologies: Models, Methods and Comparisons ()
1. Introduction
Hydrography measures the physical features of water bodies with their prediction of change over time, which includes not only bathymetry, but also the shape and features of the shoreline, the characteristics of tides, currents, waves, and the physical and chemical properties of the water for the purpose of safe navigation [1] . Bathymetry is a method of quantifying depths to study the topography of water bodies, including oceans, seas, rivers, streams, and lakes. The measurement of bathymetry using satellite imagery is one of the fundamental researches in the field of remote sensing (RS) of the marine environment, which has numerous practical applications to the coastal environment and its monitoring. Accurate determination of water depth is essential for various purposes such as monitoring underwater topography, movement of deposited sediments, and producing maritime charts for navigation. Such information is also vital for port facility management, dredging operations, and to predict channel infill and sediment budget. Bathymetric information plays an essential role in all branches of oceanography, paleoclimate studies, and marine geology. Bathymetric mapping is the process of making bathymetric maps based upon the depth data. Bathymetric maps represent the water body depth as a function of geographical coordinates, similar to topographic maps representing the altitude of Earth’s surface at different geographic coordinates. The most popular type of bathymetric maps is represented by lines of equal depths called isobaths [2] . Nowadays, bathymetry is mapped using echo sounders and the depth datasets are processed to compile nautical charts, shaded relief maps, and digital terrain/bathymetric models. Bathymetric data are generally used to generate navigational charts, 3D models, and seafloor profiles. Traditionally, ocean floor data are collected by measuring the time taken by the laser light, or an acoustic sonar pulse, to travel through the water column to the ocean floor and back, based on the speed of sound in water, sensor characteristics, time, and other variables. Spatial resolution, coverage, temporal resolution and data type vary among the different bathymetry acquisition systems [3] . Traditional bathymetric acquisition methods are capable of generating accurate point measurements or depth profiles along transects, but are constrained by their inefficiency, logistical expenses and inaccessibility in remote areas. Environmental conditions and technical restraints avoid their explicabilities to near-shore waters [4] as shallow coastal waters are perilous for navigation, especially during low tides. An alternative is to combine the shipboard and the satellite data to improve bathymetric prediction [5] . By comparison, RS method is faster and applicable to various environments, including shallow coastal waters, and clear rivers [6] . RS allows modeling of bathymetry at spatial scales that are impossible to achieve with traditional methods. Bathymetry can be estimated using RS by using several techniques, each having its own depth detection capability, accuracy/error/precision, strengths/advantages, drawbacks and best application environment [7] . The two broad categories used in remote sensing for deriving bathymetry information are active RS methods and passive RS methods. Passive RS methods employ passive sensors, which measure energy that is naturally available, e.g. multispectral or optical satellite sensors. Passive sensors record electromagnetic radiation (EMR) that is reflected (e.g., blue, green, red, and near-infrared light) or emitted (e.g., thermal infrared energy) from the surface of the Earth. However, the use of passive remote sensing for modeling water depth in fluvial environments remains a challenge [8] . Active sensors, on the other hand, transmit pulses of electromagnetic energy and record the origin and strength of the backscatter received from objects within the system’s field of view, e.g. synthetic aperture radar (SAR), and light detection and ranging (LIDAR). Advantages for active sensors include the ability to acquire measurements in all-weather and day and night conditions. Active sensors can be used for examining wavelengths that are not sufficiently provided by the sun, such as microwaves, or to better control the way a target is illuminated. Methods for derivation of bathymetry can also be categorized as non-imaging methods and imaging methods (Table 1). LIDAR and satellite altimetry are the two major non-imaging methods used for bathymetry derivation. LIDAR is elucidated as light detection and ranging, which measures the distance between the sensor and the water surface or an ocean floor using a single wave pulse or double waves. It is the time drift
![]()
Table 1. Types of non-imaging and imaging systems with their strengths and limitations (source: modified from Gao [7] ).
of the returned radiation pulses from the object at the sensed spots, which is eventually used to produce bathymetric information. However, this method is limited by the coarse bathymetric sampling interval and high cost. The basic assumption for deriving ocean bed topography from satellite altimeter measurements (non-imaging method) is summarized elsewhere [9] . The conceptual approach employs the sparse depth sounding measurements to restrict the long-wavelength depth while the shorter-wavelength topography is envisaged from the downward-continued satellite gravity measurements [10] . On the other hand, imaging methods approximate the water depth based on the pixel values or digital numbers (DN) of an image. Imaging methods make use of the visible and/or near infrared (NIR) light and microwave radiation. Radio detection and ranging (radars) are imaging sensors whilst radar altimeters and scatterometers are non-imaging sensors used for bathymetry derivation. Radar satellites use short pulses of electromagnetic radiation (EMR) in the microwave range (10 s or 100 s of GHz), therefore they do not depend on daylight and are unaffected by wind, fog, dust, clouds, and bad weather conditions. These satellites measure the radar pulses reflected from the ground surface, evaluate the signal strength or intensity to recover information on the structure of the earth’s surface, and identify the elapsed time between pulse emission and return. In case of microwave imagery, radar observes the backscattered variations from the sea surface, e.g. roughness caused by modulations in the wave spectrum with respect to the surface current [11] . Such variations in the current velocity at the ocean surface can be recognized because of interactions between tidal flow and bed topography. Although imaging method using microwave data is not subject to cloud cover, it is rather complicated because numerical inversion in place of analytical inversion is employed to derive bathymetry from speckle infested radar imagery. Additionally, its accuracy is rather low as a result of its vulnerability to wind influences [12] .
2. Remote Sensing Technologies Involved in the Derivation of Bathymetry
Various active and passive, both in the category of imaging and non-imaging, space-borne/airborne platforms can be effectively used for bathymetry derivation. Some of the most popular technologies are optical RS, LIDAR, radar Altimetry, and SAR.
2.1. Bathymetric Measurements Using Optical RS
Optical RS-based bathymetry is derived from the principle that the total amount of radioactive energy reflected from a water column is a function of water depth. Optical RS takes advantage of shortwave radiation in the blue and green spectrum that has strong penetration capabilities. As the incident solar radiation propagates through the water, it is scattered and absorbed by water molecules and in-water constituents, leaving varied energy to be emitted and recorded in RS imagery. The energy received by the sensor is inversely proportional to the water depth after removing atmospheric corrections and water column effects. Therefore, the intensity of the returned signal is indicative of the depth at which the solar radiation has penetrated. Optical RS can be implemented for bathymetry derivation using two methods; analytical modeling and empirical modeling. Analytical modeling of bathymetry is based on the characteristics of propagation of light in the water column. An analytical model is based on number of optical properties of water, such as the attenuation coefficient and backscattering are required as input parameter [7] . The flow radiative transfer model is a commonly used analytical model and it requires the input of the spectral signatures of suspended and dissolved materials, and bottom reflectance [13] . In case of empirical models, the mathematical relationship between the remotely sensed radiance of a water body and the depth at few sampled locations (ground truth) is established empirically independent of the characteristics of light transmittance in water. A strong correlation exists between water depth and the single band radiance for waters of uniform optical properties and bottom reflectance. Lyzenga [14] suggested the use of multiple spectral bands to overcome the problem of varying optical properties of the water column. The establishment of this empirical model requires a set of in-situ measurements that may include water and bottom reflectance, the vertically averaged diffuse attenuation coefficient, and the concentrations of suspended inorganic constituents, chlorophyll, and dissolved organic carbon. The field measured spectral reflectance over a wide range of wavelength is helpful to understand the most suitable band(s) for sensing bathymetry. This is especially significant in conditions of spatially varying turbidity and water qualities. In addition, other in-situ measurements may include a collection of water samples and determination of water depth at the sampling locations (determined by the GPS) using echo sounder. The least square regression analysis is used to formulate this empirical model. Regression of the observed water depth against the spectral reflectance in the most sensitive spectral band (s) is capable to yield an efficient empirical model for water depth. Applications of this model to the entire satellite image results in the generation of a bathymetric map. The empirical modeling method is valid given that the total water reflectance is related essentially to water depth, and to water turbidity [15] . This claim has been backed by Ji et al. [16] who concluded that water column scattering dominates the exit radiance from the water except if it is very shallow and transparent water bottom [7] . Optical RS methods are potentially used for derivation of bathymetry from space-borne/airborne multispectral (MS) and hyperspectral (HS) imageries.
2.1.1. Bathymetric Measurements Using MS Imagery
Coastlines, lakes, shoals and reefs are some of the most continuously varying dynamic regions of the Earth. Monitoring and measuring spatial changes are critical for understanding the environment. Near-shore bathymetry can be estimated using MS satellite imagery [17] - [21] . MS/HS imagery provides bathymetry measurements which are not reliable enough to be used for navigation purposes. However, MS/HS imagery based method is a cost effective option for bathymetry over large areas. These bathymetric products are suitable for a range of environmental and scientific applications. Imagery derived bathymetry is not directly measured, it is inferred, and as such the bathymetry is estimated, with a lower accuracy than LIDAR or multi-beam echo sounders. The depth to which the imagery is useful is limited by light attenuation. Depending on water clarity, depths derived from aerial or satellite imagery are limited to 25 - 30 m because of light penetration issues [22] . There are two recognized techniques for deriving bathymetry using MS satellite imagery: 1) radiometric approach and 2) photogrammetric approach [23] .
1) Radiometric approach for deriving bathymetry: The radiometric approach exploits the fact that different wavelengths of light are attenuated to different degrees by water, with red light being attenuated much more quickly than blue light. RS technologies have exceeded the capability of existing MS satellite to detect light in the blue (450 - 510 nm), green (510 - 580 nm) and red bands (630 - 690 nm) to achieve superior estimates of depth, in water up to 15 meters deep. In addition, with the help of sound navigation and ranging (SONAR) based in-situ measurements, it is possible to achieve vertical and horizontal accuracies of less than 1 meter. Currently, airborne or space-borne high-resolution MS platforms are employed in order to improve bathymetric measurements, e.g. WorldView-2 (WV-2). These sensors are capable to detect light between 400 and 450 nm wavelengths ? the EMR spectrum that provides the deepest penetration of clear water. Several studies using these datasets have shown that accurate and precise bathymetric quantification can be achieved up to 20 meters and deeper. WV-2 is the first industrial high-resolution satellite to provide 1.84 m resolution MS imagery, plus a coastal blue spectral band focused on the 400 - 450 nm range, which can be used for bathymetric measurements with substantially improved depth and accuracy [24] -[29] . Large synoptic collections, enabled by WV-2 agility and rapid retargeting capabilities, allow to evaluate the differing absorption of the blue, coastal blue, and green spectral bands, and to calibrate their bathymetric measurements using a few in situ points, and then consistently extend the model across the entire study area.
2) Photogrammetric approach using digital elevation model (DEM) for deriving bathymetry: In this method, stereoscopic images can be collected over the target area, a DEM [30] or digital bathymetry model (DBM) of the shallow ocean floor can be produced from the imagery. Early studies with both satellite imagery and digital photography appeared promising, and reveal that this method can be used to generate accurate bathymetric models of shallow environments without in situ data. However, the method has not been widely studied because of the limitations in the capabilities of current sensors. The challenge in collecting stereoscopic imagery of the shallow ocean floor is to understand the interaction of light with the air/water interface. At high angles of incidence, the light is entirely reflected off the surface of the water, preventing any observation of sub-aquatic features. Present multispectral satellite sensors are not capable to collect enough high-resolution stereoscopic imagery within the narrow angle needed to penetrate the sea surface. In addition, none of them is capable to provide shorter wavelength blue light necessary for maximum depth penetration. WV-2 can be used for implementing this new method for measuring bathymetry. The Coastal Blue band can deliver maximum water penetration and WV-2’s enhanced agility enables the acquisition of enormous amounts of high-resolution in-track stereo imagery at the ideal angle for water penetration. The advantage of this approach is that numerous images can be co-registered using tie points that are visible on land and water, and the resulting stereo composite can be used to calculate the water depth without relying on in situ measurements. [31]
2.1.2. Bathymetric Measurements Using HS Imagery
With the advent of HS scanners [32] which sample the upwelling radiance spectrum in several tens of bands which have water penetration, more spectral discrimination power can now be brought to bear on the coastal optics problem. HS methods facilitate to discriminate more independent environmental variables than multi-spectral methods. HS imagery is more complex than MS imagery. The derivation of bathymetry from HS imagery is still under development. The increased number of spectral bands used by HS sensors enables the discrimination between different components of the water column and sea bed. However, this extra complexity has restricted its applicability to the research application [33] . The additional spectral bands enable a more accurate evaluation of water depth and bottom type than is possible from the MS sensors discussed in the previous section. HS imagery is still largely acquired using airborne acquisition methods and so does not have the advantages associated with satellite imagery. The first HS sensor in space, Hyperion, has been used for mapping shallow water benthic habitat [34] . Airborne hyperspectral instruments can also provide the spectral and spatial resolutions needed for deriving bathymetry. However, the cost of acquisition is higher, to the point of limiting the usage of HS airborne imagery in mapping large coastal areas. Increased developments and launches of satellite-based HS sensors will make this acquisition technique more feasible for large area bathymetry processing. As an airborne technique, the advantages for deriving bathymetry from HS sensors are limited compared to other available airborne technologies. There is no easily identifiable depth, coverage or environmental advantages to airborne HS imagery derived bathymetry over LIDAR-based bathymetry.
2.2. Bathymetric Measurements Using LIDAR
The practicability of deriving water depths using airborne blue-green laser pulse was established as early as the late 1960s [35] . Lyzenga [36] pioneered the use of LIDAR in shallow water bathymetry. Airborne LIDAR is superior for mapping seafloor topography in coastal waters with low in-water constituents (suspended sediment concentrations or organic pigments) [37] . LIDAR bathymetry is an active non-imaging RS sensor that involves the transmission of laser light pulse using infrared and green wavelengths of the EMR spectrum [38] [39] . A laser altimeter onboard an aircraft pulses both of these waves to the water surface and measures the time lapse for the energy to return. The infrared light is reflected back to the sensor from the water surface while the green light penetrates through the water column. The water depth is estimated from the time difference between the infrared and green laser reflections using simple mathematical calculations that incorporate the characteristics of the water column along with system and environmental parameters. In LIDAR-based bathymetry systems, longer wavelength radiation is not ideal because of increasing absorption by water. Also, shorter wavelengths are not ideal because of strong scattering and absorption by in-water constituents, which causes shallower penetration in the water column [40] . Bathymetric LIDAR data are typically very dense, with millions of data points. Point spacing can vary from centimeter to several meters, which can be used to generate high resolution digital elevation or bathymetry models (DEMs or DBMs) to supplement SONAR or eco-sounding data for hydrographical and navigational purpose. The spatial resolution of depth measurements collected by LIDAR bathymetry systems depends on two principal variables; (a) the physical characteristics of the LIDAR sensor/laser scanner and scanning instrument, and (b) water depth. LIDAR based bathymetry systems are capable of measuring water depth from 1.5 to 60 m [41] at an accuracy up to 15 cm. The aircraft altitude above the water surface plays an important role in the spatial resolution of the footprint of the seafloor. The temporal resolution of the airborne LIDAR is limited by the episodic nature with which the surveys are carried out. The accuracies associated with the LIDAR bathymetry are quite high. Bathymetric LIDAR systems receive both image-based and discrete vector data. The actual signal received by the receiver is a waveform, and the properties of the waveform may vary from one sensor to the other. A variety of types of data transformations can be derived from the source data to establish models to represent bathymetry. The actual water depth is simply a difference between the two peaks of the waveform depicting the two surfaces, i.e., maxima of the two main signals [39] . Depth measurements captured as a point can undergo further data processing for modification of the ocean floor model and to account for any systematic errors introduced during the collection process. Based on the intensity of the signal from the ocean floor, LIDAR can also compute the surface difference between ocean surface and ocean floor. The reflectance values are captured as a digital number (DN) value stored as a raster format associated with the depth measurement [3] .
2.3. Bathymetric Measurements Using LIDAR
Analogous to MS and HS imagery which deduce depth, SAR does not directly measure bathymetry; it infers depth from changes in the sea surface [12] [42] . This enables SAR to provide a potential solution in turbid aquatic environments where other RS techniques are unsuccessful. However, SAR is one of the less frequently used technologies employed to determine near-shore bathymetry and the technique is not currently reliable enough to be used as a supplementary technology in bathymetry gaps caused by turbidity. Under favorable meteorological and oceanic hydrodynamic conditions (moderate winds and strong tidal currents), air and space borne SAR imagery can be used to identify features of the bottom topography of shallow seas [43] [44] . SAR bathymetry determination is based on its capability to quantify the change in height and roughness of the sea surface. The rougher water enhances the radar backscatter giving a brighter zone on the radar image [42] [45] . Practical operation SAR bathymetric measurement requires knowledge of the tidal currents and the wind, as the wind speed and direction affects the roughness modulation. The SAR imaging mechanism consists of three steps: a) the interface between (tidal) flow and bottom topography results in the inflection of the surface flow speed. This relation can be illustrated by numerous models with an increasing level of complications such as: continuity equation, shallow water equations, etc., b) modulations in the surface flow velocity cause deviations in the surface wave spectrum, which can be modeled with the action balance equation, and c) a deviation in the surface wave spectrum causes variations in the level of radar backscatter. Bragg model two-scale and first iteration Kirchhoff model can be used to compute the backscatter deviations. More detailed mathematical illustration is found elsewhere [46] . SAR has the benefit of being unaffected by atmospheric disturbances and cloud cover. SAR produces relative bathymetry, rather than absolute depths. The technology is particularly suited to areas of sandbanks and shoals where there are continuous changes in bathymetry. However, there are several uncertainties inherent in the measurement and manipulation of SAR bathymetry observations used to estimate ocean depth. These make SAR derived bathymetry difficult to determine and inherently unreliable compared to other technologies.
2.4. Bathymetric Measurements Using Altimetry
Satellite altimetry can be used to determine the gravity field of the oceans on a global scale. Gravity field data can be used to approximate the bathymetry of deep-seafloor features, e.g. seamounts and ridges. Dense satellite altimeter measurements can be used in combination with sparse in situ depth soundings of the seafloor to compile a uniform resolution bathymetric map of the seafloor topography. These maps have comparatively low accuracy and resolution to be used for assessing navigational hazards, but these maps can be useful for various applications, e.g. locating obstructions to the major ocean currents and shallow seamounts. Altimetry-derived bathymetry also reveals plate boundaries and oceanic plateaus. The basic theory for deducing seafloor topography from satellite altimeter measurements is summarized elsewhere [9] . The conceptual approach uses the sparse in situ depth soundings to restrict the long-wavelength depth while the shorter-wavelength topography is inferred from the downward-continued satellite gravity measurements [10] [47] . There are a number of complications that need careful handling; the most important ones are 1) computing bathymetry from gravity anomalies is possible over a limited wavelength band, and 2) longer wavelengths are highly dependent on the elastic thickness of the lithosphere. The feasibility study of a bathymetry calculation technique based on the one-dimensional filtering of SEASAT tracks is published elsewhere [9] . Fundamentally, the algorithm is based on the linear approximation of the relationship between the geoid and a given density contrast interface. Several algorithms are developed to derive bathymetric predictions from satellite altimeter. The most popular methods are: 1) the one-dimensional inversion of satellite tracks using linear approximation of the transfer function [9] [48] [49] , 2) the one-dimensional adjustment of synthetic and satellite tracks [50] , 3) the geometrical analysis of satellite tracks [51] , 4) the two-dimensional inversion of geoid anomalies [52] , and 5) the two-dimensional inversion of satellite data and the merging with conventional geophysical measurements [10] [53] [54] .
3. Methods for Derivation of Bathymetry Information Using RS Technology
Numerous algorithms have been developed for deriving bathymetry information from multispectral and hyperspectral imageries, SAR imageries, and LIDAR data. Some of the most important algorithms are described in the following section;
3.1. Derivation of Bathymetry Using Optical Remote Sensing Models
Following are the most commonly used algorithms for calculating the bathymetry from multispectral and hyper- spectral imageries.
3.1.1. Stumpf Model/Linear Ratio Model
Stumpf et al. [55] proposed a “Ratio method” to overcome the drawbacks of changing substrate albedo in deriving bathymetry information. The model is based on the theory of light attenuating exponentially with depth, and proposed that the effects of substrate albedo are minimized using two bands to derive the depth. This principle is explained mathematically as follows:
 (1)
(1)
where Z is depth, g is a function of the diffuse attenuation coefficients for both downwelling and upwelling light, Ad is the bottom albedo, R∞ is the water column reflectance if the water were optically deep, and Rw is observed reflectance. The ratio model addresses the drawback by comparing the attenuation of two spectral bands against each other rather than using albedo as a variable in depth derivation. Different spectral bands attenuate at different rates. Therefore, the ratio between two spectral bands will vary with depth. The modification in the bottom albedo should affect both spectral bands equally, but the modification in attenuation with depth will be greater than the alteration attributable to bottom albedo so that the ratio between two bands should remain comparable over different substrates at the similar depth. This can be illustrated mathematically as follows:
 (2)
(2)
where, Z is depth, m1 is a tunable constant to scale the ratio to depth, n is a constant to ensure the ratio remains positive under all values, Rw is observed reflectance, and m0 is the offset for a depth of m0. The ratio transform method addresses several issues that have substantial significance to use passive MS imagery to map shallow-water bathymetry. First, 1) it does not require subtraction of dark water pixels, 2) the ratio transform method has fewer empirical coefficients required for the solution, which makes the method easier to use and more stable over broad geographic areas, and 3) the ratio method can be tuned using available reliable depth soundings.
3.1.2. Jupp’s Model or Depth of Penetration Zone (DOP) Model [56] [57]
A model that finds large usage in literature to reconstruct the bathymetry in coastal zones from MS imagery is the depth of penetration zone (DOP) method proposed by Jupp [56] . There are two parts to Jupp’s method: 1) the computation of DOP zones, and 2) the interpolation of depths within DOP zones. The method [56] has three critical assumptions: 1) attenuation of light is an exponential function of depth, 2) water quality does not vary within an image, and 3) reflective properties of the substrate are constant. The second and third assumptions are the weakness of this model because in some cases water and seabed properties fluctuate, as the satellite image normally covers a very large area. Considering a bunch of monochromatic light, the relative loss of radiant flux is proportional to the size of the path, to less of a coefficient of proportionality (extinction coefficient). Jupp’s model can be mathematically expressed as:
 (3)
(3)
where Le is measured at-sensor radiance, Lb is the emergent radiance from the seabed, Lw is the emergent radiance from different layers of water, z is depth, k is the coefficient of absorption. If the term Lw is hypothesized as negligible and is directly related to the quality of the water (suspended sediments) and small changes in the seabed, then, among the depth of the water column and the logarithm of the measured at-sensor radiance, there will be a linear relationship. Under these conditions, rearranging Equation (3) lead to the classical DOP equation for the water depth determination:
 (4)
(4)
where N is the number of spectral bands. In practice, to guarantee homogeneity, the DOP model assumes constant coefficient of absorption, which is the main cause of the failure of the DOP algorithm in some cases, where the spatial lack of homogeneity is very high.
3.1.3. Lyzenga Model or Linear Band Model
Satellite RS data is the amount of light reflected, which is affected by the atmosphere, water clarity, depth attenuation, bottom reflectance, scattered suspended material and so on [58] . Campbell [59] described that the sunlight spectrum has different penetrability, bottom reflectance and suspended material scattering. Therefore, to advance the accuracy of water-depth estimation, the RS data can be classified using multiband radiance. In ideal conditions, under the assumptions of a homogeneous atmosphere, similar wave situation, similar water property, and homogeneous bottom property, the water depth can be retrieved from a satellite. After penetrating the water column, the satellite sensor detects the visible light reflected from the bottom. In the water column, the light is attenuated exponentially with depth by Beer’s Law and the relationship of observed reflectance to depth and bottom albedo could be described as [55] [60] ;
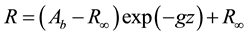 (5)
(5)
where R∞ is the water column reflectance, if the water is optically deep, Ab is the bottom albedo, z is the depth, and g is a function of the diffuse attenuation coefficients for both down-welling and up-welling light. However, the derivation of depth from a single band is dependent on the albedo Ab, with a decline in albedo resulting in amplification in the estimated depth. Lyzenga [36] proposed a linear solution of correction for albedo with two bands as;
 (6)
(6)
where 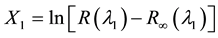 and λ is the wavelength. The algorithm corrects for a range of variations in both water attenuation and bottom reflectance using a linear combination of the log-transformed radiances in the blue and green channels. Lyzenga model has essentially attempted to account for unpredictability in bottom type by using multiple spectral bands. A variable, Xj, was defined for each of the N bands as:
and λ is the wavelength. The algorithm corrects for a range of variations in both water attenuation and bottom reflectance using a linear combination of the log-transformed radiances in the blue and green channels. Lyzenga model has essentially attempted to account for unpredictability in bottom type by using multiple spectral bands. A variable, Xj, was defined for each of the N bands as:
 (7)
(7)
where, Lj = above-surface reflectance in band j and Lwj = averaged deep-water reflectance. The reflectance values were log-transformed to create a linear relationship between input reflectance and depth. Deep-water reflectance was used to account for reflection because of surface effects and volume scattering in the water column and was assumed to result mostly from external water reflection, including sun-glint effects, and atmospheric scattering. However, the effect of deep water radiance was almost negligible in shallow water bodies. To account for water quality heterogeneity and depth-independent variability in reflectance values between bands this algorithm was updated by Lyzenga [36] , and again Lyzenga et al. [61] . This produced (N + 1) depth-indepen- dent variables that could be used as indices of bottom type, and finally modeled depth as:
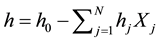 (8)
(8)
where ho and each hj are constants defining a linear relationship between Xj and depth. ho and all of h1 to hj are determined through multiple linear regression between a set of known depths and the log-transformed reflectance values found at those depths. The method increases operational flexibility since wavelength bands are not restricted by the algorithm.
3.2. Derivation of Bathymetry Using LIDAR Models
To map large linear bathymetry rivers, bathymetric LIDAR is a suitable RS technique, complementary to SONAR [62] . Most of the research works carried out by different authors was based on comparing the optical modeling results with LIDAR bathymetry results where the accuracy of optical models was compared to LIDAR bathymetry results.
Bathymetry Estimation on a Simulated Green LIDAR Full Waveform (GLFW)
A procedure for estimating the bathymetry (Ĥ) from peaks detection of surface and bottom on a simulated GLFW was developed using an approximation method. This approximation is classically based on a mixture of Gaussians laws fitted by an iterative least squares optimization algorithm. With approximation, water depth Ĥ can be estimated from a simulated GLFW having a real depth H. The method is based on three major steps: (1) Minimum depth determination, (2) Confidence interval of the minimum depth detectable. (3) Comparison of the values according to surface roughness parameters. Using this model waveforms can be generated and analyzed using a classical approximation method of water depth. Results for a flat water surface and a moderate roughness show a minimal depth detectable of 0.41 m [62] [63] .
3.3. Derivation of Bathymetry Using SAR Models [64]
3.3.1. Wave Tracing Method [64]
Fast Fourier transformation (FFT) is a technique used to decompose a function in spatial domain into its constituent frequency components. It can be very useful while obtaining regular periodicity in the images. FFT can also be used for retrieving the wavelength and wave direction of the ocean surface waves. The FFT of a SAR sub image of N × N pixel size gives a 2-D image spectrum. The peak in this spectrum represents the mean wavelength and the mean wave direction. The wavelength and angle of propagation can be estimated using:
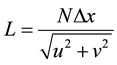 (9)
(9)
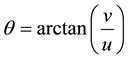 (10)
(10)
where L is the measured peak wavelength, θ is the peak wave direction, Δx is the spatial resolution of the subset image, N is the size of the sub-image, and u and v are the coordinates of the dominant frequency with the centre point as origin.
3.3.2. Linear Dispersion Relation
The water depth (D) for the particular FFT box can be retrieved from linear dispersion relation
 (11)
(11)
where L is the peak wavelength, ω is the peak frequency (ω = 2π/t), t is the peak period, and g is the acceleration due to gravity. The peak period should be estimated by the analysis of the wave tracks and by the first measured wavelength of a wave ray along with the first guess for the water depth.
4. Review on Case Studies Employed for Bathymetry Derivation
As bathymetry derived from imagery is estimated rather than directly measured, it is worth discussing the influence and impact of the algorithms used to model the depths. A number of different algorithms have been derived to determine bathymetry from imagery. For HS and MS imagery derived bathymetry, it is just as important to select the most appropriate algorithm, as it is to select the most suitable image sensor. Mobley [65] compared six common algorithms used to derive bathymetry. Few case studies are discussed for comparison of methods, models, algorithms, and types of data used for derivation of bathymetry (Table 2).
5. Summary and Discussion
The seafloor is one of the last mostly unexplored and most dynamic landscapes on the planet earth. Technological development for bathymetry derivation has progressed rapidly in the last century because of the advancement of techniques using acoustics, optics, and radar. More acoustic depth soundings are required to validate RS based models for the derivation of bathymetry in remote regions of the world (e.g. Southern Ocean, around Antarctica, Arctic, etc.). The present review focuses mainly on techniques used for deriving the bathymetry, methods and technologies evolved for bathymetric derivation, and limitations and advantages of bathymetric algorithms. There are two broad ways in which RS methods for bathymetry derivation can be categorized: active RS/passive RS and non-imaging/imaging. The non-imaging LIDAR method is capable to detect elevations at sampled locations, but this method is not widely used for practical applications until recently because of technical constraints. LIDAR method is capable to derive a large range of depths up to 70 m in clear open waters with an accuracy of ±15 cm [7] . Airborne LIDAR is appropriate for bathymetric mapping over relatively small geographical areas. LIDAR accuracy and applicability are additionally constrained by water turbidity. In comparison, the passive optical imaging method is more flexible, because it can be implemented either analytically or empirically. Analytical modeling is complex to implement since it requires the input of in-situ measured parameters related to the optical properties of water. Empirical modeling is much easier to implement, since it requires only a limited number of in-situ measurements at certain sampling spots. This implementation may produce results which have similar accuracy to the analytical or semi-analytical implementations under certain circumstances. The passive imaging methods are widely applicable to both shallow turbid coastal waters and open oceanic waters. It is just important to select the most appropriate bathymetric algorithm, as it is to select most suitable image sensors for an effective derivation of bathymetry. Each model or sensor has benefits and limitations. For most of the case studies, optical data, such as WV-2, QuickBird, SPOT, Landsat and IKONOS, have been used [15] [20] [30] [55] [57] [61] [66] -[85] .
In general, Lyzenga model (linear band model) used for QuickBird data can yield the error of water depth about 9.7%, while for IKONOS the RMS is ≈2.3 m [72] . The Lyzenga algorithm corrects for a range of variations in both water attenuation and bottom reflectance using a linear combination of the log-transformed radiances in the blue and green spectral channels. The Stumpf model or ratio transform model can retrieve depths in less than 25 m of water [55] . It also performs better in scattering turbidity than the linear band model. The ratio model is found to be somewhat nosier and cannot always adequately resolve fine morphology in water depths less than 15 - 20 m. In general, the ratio transform was found to be more robust than the linear transform [55] . In a few cases three models viz. Jupp’s, Stumpf and Lyzenga were used, where the depth was found to be less than 30 m with different methodologies used. The empirical model (SPOT-5 imagery) can yield the accuracy of 0.5 m based on in-situ data [15] . In shallow waters, empirical fitting is time-efficient, but requires real-time high- density depth soundings to provide precise results. In case of semi-analytical model (SPOT-5 imagery), the computed depths were found to be underestimated when water depth exceeded 2.5 m. In general, bathymetry derivation accuracy was observed to be depth dependent; more errors were observed at greater depths. In general, there are several benefits as well as limitations of optical RS models used for mapping the bathymetry. Two
![]()
Table 2. Summary of case studies utilizing various satellite datasets and methods for bathymetry derivation.
of the algorithms (Linear/Lyzenga and Ratio/Stumpf) are found to be superior to accurately determine the shallow depth in highly turbid waters given sufficiently representative training data sets. The ratio transform method or Stumpf model has less number of empirical coefficients which makes the method simple to use and more stable over broad geographic areas. The ratio model is more robust in case of the non-homogenous environment. The ratio transform has limitations relative to the linear transform, particularly in an increased level of noise. On the other hand, Lyzenga linear band model employs two or more bands, which allows separation of variations in depth from variations in bottom albedo, but compensation for turbidity. Retrieval of bathymetry under restrictive environmental conditions is limited. The linear band algorithm modified from Lyzenga et al. [61] can provide slightly better results than Stumpf model using WV-2 data. The additional 4 spectral bands provided by the WV- 2 have been found to be improved the linear band model marginally. A classification using band instead of raw band values achieved results comparable to the linear band algorithm. Although its data input requirements are the same as the more accurate band classification, its lower computation requirements may make it attractive after further validation. The linear ratio algorithm developed by Stumpf et al. [55] may prove completely ineffective in waters where turbidity is the predominant factor defining attenuation in the water column. In order to achieve better results using the linear ratio model, ground reference or in-situ datasets should be considered to represent a wide range of variance in bottom type and water column properties with statistically significant sample sizes at different depths.
Acknowledgements
We acknowledge Dr. S. Rajan, Director, NCAOR for his encouragement and motivation of this research. We acknowledge Dr. T. P. Singh (Director, SIT), Dr. Kanchan Khare (HOD, Department of Civil Engineering, SIT), Prof Sagar Kolekar (SIT), and Prof. Rushikesh Kulkarni (SIT), for their cooperation. We also thank Ms. Prachi Vaidya, India for her constructive comments on the draft version of the manuscript. This is NCAOR contribution No. 17/2015.