Modeling and Simulation of Hot Metal Desulfurization by Powder Injection ()
1. Introduction
Current industrial consumers demand high quality steels with tight chemical specifications, superior mechanical performances and low impurity contents. Particularly, sulfur is a detrimental impurity which causes brittleness and granular cracks in steels and adversely affects mechanical properties such as ductility and impact toughness. Therefore, hot metal from blast furnaces must be treated prior to the oxygen steelmaking in order to obtain steels with low sulfur contents [1] . In the desulfurization process, powdered reagents are injected into the hot metal through an immersed lance using an inert carrier gas such as argon or nitrogen, as shown in Figure 1. The reagents chemically react with the dissolved sulfur forming a sulfide that ascends and is captured in the slag layer that covers the melt. Lime, calcium carbide and magnesium are the powdered reagents commonly employed for the hot metal desulfurization [2] .
Nowadays, some technology suppliers are offering to steelmakers desulfurization systems based on the simultaneous injection, namely co-injection, multiple-injection or mono-injection of diverse powdered reagents
![]()
Figure 1. The desulfurization process of hot metal by powder injection.
for manufacturing ultralow sulfur steels [3] -[5] . They promise market-driven innovation, enhanced injection process, flexible production execution, highest availability, cost reduction, and so on [3] . Many experimental [6] -[9] and numerical [10] - [13] works have been published in the specialized literature concerning the hot metal desulfurization. Some of them [14] [15] report mathematical models on co-injection of desulfurization using several powders; however they are so complex that practical applications by plant engineers are hard to implement.
In this work, isothermal mathematical models to simulate the hot metal desulfurization by the mono-injection of lime powder and the co-injection of lime, calcium carbide and magnesium powders are developed and presented. The mono-injection model is derived from the continuity equation and is validated using experimental results and data from literature. Computational fluid dynamics (CFD) simulations are carried out to verify the simplification assumptions made to the continuity equation. The co-injection model uses a rate constant for the mixture which is determined from the molar fractions and rate constants of the individual powders. The effect of the lime content of the mixture on the desulfurization dynamics and reaction half-life is analyzed.
2. Mono-Injection Desulfurization Modeling
The equation of continuity in cylindrical coordinates [16] can be employed to mathematically represent the desulfurization process:
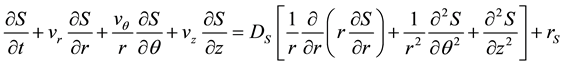 (1)
(1)
where S is the sulfur concentration in hot metal, t is time, and r, θ and z are the radial, the angular and the axial components of the cylindrical coordinates, respectively; vr, vθ and vz are the components of the velocity vector in the r, θ and z directions. Besides, rS is the rate of disappearance of S by chemical reaction and DS is the diffusion coefficient of sulfur in the hot metal.
Given that the bubbles of the carrier gas are mainly moving in the axial direction, one can assume that the desulfurization phenomenon is predominant in that direction; then Equation (1) is reduced to
 (2)
(2)
Furthermore, considering that: 1) the diffusion of sulfur is small compared to its convective transport and 2) the vessel is a well stirred tank with small concentration gradients, then Equation (2) is simplified to an ordinary differential equation:
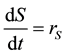 (3)
(3)
The desulfurization reactions are first order chemical reactions whose kinetics can be expressed as follows [17] :
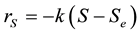 (4)
(4)
where k is the reaction rate constant and Se is the value of the sulfur concentration at thermodynamic equilibrium. The reaction rate constant is a temperature-dependent term which is well represented by Arrhenius’s law [18] :
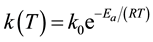 (5)
(5)
where k0 is the pre-exponential constant, Ea is the reaction activation energy, R is the universal gas constant and T is the absolute temperature.
Substituting Equation (4) into Equation (3) and integrating one obtains
 (6)
(6)
where S0 is the initial concentration of S.
3. Desulfurization with Mono-Injection of Lime Powder
In addition to its dependence on temperature, rate constant of Equation (6) depends on a lot of factors, such as lime particle diameter, carrier gas bubble diameter, residence time of particles, hot metal density, hot metal viscosity and so on. In [17] , the rate constant for lime desulfurization is determined from
 (7)
(7)
where β is the mass transfer coefficient, tR is the mean residence time of lime particles in the melt, qCaO is the lime flow rate, ρM is the hot metal density, dp is the lime particle diameter, wM is the hot metal weight and ρCaO is the lime density.
Given that the lime particles are upwards transported by the carrier gas bubbles, the mean residence time of the particles can be estimated from the rise velocity of the gas bubbles vb:
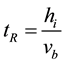 (8)
(8)
where hi is the immersion depth of the injection lance. The rise velocity of argon bubbles is estimated here from the well known Stoke’s law:
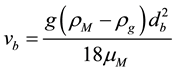 (9)
(9)
where g is the gravity constant, ρg is the carrier gas density, db is the bubble diameter and μM is the melt viscosity.
4. Validation of the Mono-Injection Model
The mono-injection mathematical model is validated using the results reported in [17] for the desulfurization of hot metal with lime in a cylindrical ladle of 150 metric tons of hot metal with an initial sulfur concentration of 0.1 weight percent and 2400 s of injection time. The remainder parameters are shown in Table 1.
From the parameter values of Table 1, the following values of the rate constant, the bubble rise velocity and the mean residence time, respectively, are obtained: k = 0.001684 s −1, vb = 0.7938 m s−1, tR = 2.52 s. Figure 2 shows a comparison between the results of [17] and the present mono-injection model using Equation (6). The observed agreement is fine, and this gives good confidence in the results of the subsequent co-injection simulations.
In order to verify the assumption that the vessel is a well stirred tank, isothermal transient 2D Computational Fluid Dynamics (CFD) simulations are carried out using the parameter values given in Table 1. The equations of continuity and momentum, the Volume of Fluid (VOF) model for multiphase flow and the classical K-ε model for turbulence modeling are employed in the CFD simulations [19] . The boundary conditions for K and ɛ in
![]()
Table 1. Parameter values employed in the mono-injection model validation.
![]()
Figure 2. Comparison between results of [17] and the present model.
the lance nozzles are determined from the expressions.
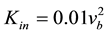 (10)
(10)
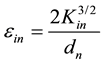 (11)
(11)
where dn is nozzle diameter.
For dn = 0.02 m and a lance with two nozzles, Equations (10)-(11) yield Kin = 0.0063 and ɛin = 0.05. For an injection angle of 45 degrees, the velocity components of vb are as follows: for the left nozzle, vx = vy = −0.5613 m∙s−1; for the right nozzle, vx = 0.5613 m∙s−1, vy = −0.5613 m∙s−1.
Figure 3 shows the distribution of phases for t = 5 s. The argon bubbles ascend to the hot metal surface in the vicinity of the walls of the immersion lance, however many bubbles spread to the vessel walls, mainly in the upper section of the ladle. Given that the ascending bubbles cause convective movement and agitation of the hot metal, Figure 3 suggests that the assumption of considering the vessel as a well agitated tank is valid. This assumption is corroborated with the corresponding hot metal streamlines depicted in Figure 4, where significant hot metal agitation in the vessel bottom is observed.
5. Co-Injection Desulfurization Modeling
Desulfurization of hot metal by co-injection with three powders: lime (CaO), calcium carbide (CaC2) and magnesium
![]()
Figure 3. CFD simulation of argon bubbles (yellow) ascending through the hot metal (red).
![]()
Figure 4. Streamlines in the hot metal produced by the argon ascending bubbles.
(Mg), is considered in this work. The corresponding desulfurization chemical reactions are as follows [1] :
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
where ( ) and [ ] means the slag and the metal phase, respectively. In Table 2 are shown the individual rate constants of the powders considered.
Mathematical modeling of powder co-injection is not an easy task given that several reagents are reacting simultaneously with sulfur, each one with its own rate constant and physicochemical properties. In this work a mixture rate constant is proposed based on assigning a weight to each individual powder in accordance to its mol fraction in the co-injected mixture:
![]() (15)
(15)
where km is the rate constant of the co-injected mixture, xi is the mol fraction of the ith powder, ki is the rate constant of the ith powder, and n is the number of powders injected. Five mixtures are considered for co-injection, whose weight percent composition and rate constants are shown in Table 3. As is observed, the rate constant depends on the proportion of powders in the mixture. Table 3 shows that the reaction constant of the mixture decreases as the lime content is increased.
6. Results and Comments
Results for the mono-injection of the powders considered are depicted in Figure 5 using an initial sulfur concentration of 0.1 weight percent. This figure shows that, among the three powders considered, lime yields the slowest dynamics for desulfurization, particularly during the first half of the injection process. At the end of the injection, the final sulfur concentration is low and similar for calcium carbide (0.0002773 wt%) and magnesium (0.0002863 wt%), whereas for lime is relatively high (0.00176 wt%). Figure 5 suggests that calcium carbide is the most efficient desulfurization powder from the chemical kinetics viewpoint, followed by magnesium, however, their cost prevents their wider usage in plants.
Results of numerical simulations for co-injection using the mixtures of Table 3 are seen in Figure 6. The fastest desulfurization dynamics occurs for the mixture number 1, whose lime content is null. As the lime content in the mixture is raised, the sulfur concentration in the hot metal exhibits a slower decay. This is explained by the fact that the mixture rate constant decreases as the lime content is increased, as is observed in Table 3.
The half-life of a chemical reaction, th, is defined as the time needed for the concentration of reactants to drop to one-half the initial value [18] . For a first order chemical reaction th is determined from the expression
![]() (16)
(16)
![]()
Table 2. Reaction rate constants of the powders considered.
![]()
Table 3. Co-injected mixtures and average rate constant.
![]()
Figure 5. Mono-injection desulfurization of hot metal with lime (solid line), calcium carbide (dotted line) and magnesium (dashed line) powders.
![]()
Figure 6. Desulfurization behavior under co-injection using the mixtures of Table 3.
![]()
Figure 7. Half-life of the desulfurization reaction as function of the lime content in the co-injected mixture.
Essentially, th evaluates the slowness of a chemical reaction in this way: as th is increased, the slower the reaction becomes. This concept is applied here to the co-injection desulfurization process using the mixture rate constants of Table 3, and results are shown in Figure 7 as function of the mixture lime content. It is observed that as the lime content in the mixture is increased, th is decreased. This result is consistent with the results of Figure 6.
7. Conclusions
The mono-injection and the co-injection desulfurization of hot metal with powdered reagents is mathematically modeled in this work assuming that the diffusion of sulfur is small compared to its convective transport and that the vessel is a well stirred tank with small concentration gradients. Lime, calcium carbide and magnesium powders are considered in the co-injection process. From the isothermal numerical simulations the following conclusions arise:
1) The bubbles of the carrier gas promote the agitation of the bath, and CFD simulations corroborate the validity of the well stirred tank assumption which allows the simplification of the continuity equation.
2) The mono-injection desulfurization model using lime powder is validated with data previously reported in the literature, and represents properly, in a quantitative way, the corresponding process. This model takes into account those parameters that are significant from the physical and chemical points of view.
3) A simple model based on the molar fraction and rate constant of the individual powders is proposed to determine the rate constant of the co-injected mixture.
4) Lime content of the mixture determines the speed of the co-injection desulfurization dynamics. This is more evident in the first half of the process. As the lime content of the lime-calcium carbide-magnesium mixture is increased, the half-life of the desulfurization chemical reaction is increased.
5) The numerical results suggest that, in order to increase the co-injection desulfurization rate, the lime content in the mixture must be reduced. Among the powders considered, lime is the cheapest one. However, previous to make a decision in the plant about the lime content, a deep analysis must be carried out by each steelmaking shop in order to balance economical, technical and productivity factors.