Applied the Large Scale Particle Image Velocimetry Technique for Measurement the Velocity of Gravity Currents in the Laboratory ()
1. Introduction
A gravity current is the flow of one fluid driven by the gravity into another fluid with a different density [1] . Gravity currents frequently occur in both natural and artificial situations: thunderstorms, sea-breeze fronts, estuarine effluents, discharge of industrial waste waters into rivers, lakes or oceans, sudden release of foreign gas into the atmosphere, etc. [2] . Gravity currents are also horizontal flows which can be created by a temperature difference, a salinity contrast or suspended materials. The release of pollutants into rivers, oil spillage on the sea environment and desalination plant outflows is a few of man-made gravity currents that occur in water masses and frequently cause negative environmental impacts. The first theoretical study on gravity currents was performed by Von Kàrmàn [3] .
A video imagery technique for making flow measurements in streams and waterways is presented and used to estimate discharge for river. A video camera was used to visualize the flow seeded with tracers. Measurements of free surface flow velocities were then made using particle image velocimetry (PIV) techniques [4] . New technologies have been developed for discharge and surface velocity measurements due to concerns about flow conditions, costs, accuracy, inaccessible locations, measuring time and the safety of conventional methods. One emerging technology is large-scale particle image velocimetry (LSPIV), which has several advantages over con- ventional measurement techniques; namely, LSPIV is safer, non-intrusive and provides continuous measurements [5] .
Taylor was the first to show analytically and experimentally that longitudinal dispersion is determined by the time-averaged, three-dimensional velocity profile and the transverse molecular or turbulent diffusion [6] -[8] . The velocity estimation principle implemented in the device is an adaptation of the particle image velocimetry (PIV) technique widely used in experimental fluid mechanics measurement of flow velocities [9] [10] . The technique used in this work is a direct outgrowth of the conventional PIV used for images large-scale flow surface and was therefore dubbed large-scale particle image velocimetry (LSPIV) [11] .
The local velocity and vorticity fields are measured using an optical technique similar to large scale PIV (LSPIV) based on an intercorellation function of two images [11] [12] . The use of the LSPIV technique in field applications is now widespread after the pioneering work of [11] [13] and has been significantly improved [14] [15] .
In this paper, we describe velocity flow measurement in laboratory. The approach involves two steps: 1) surface velocity measurement using video imagery techniques, and 2) as such, the configuration studied here can represent a process of coastal discharge of effluents. Surface velocity measurements are made using particle image velocimetry, as well established technique in fluids research for laboratory flow measurement.
We applied the image processing and the spatiotemporal diagrams technique in order to describe the time evolution of the progress x, and the spreading y of the gravity current. That means able to measure these two components which characterize the flow of the gravity current as a function of the flow rate and salinity (Froude number).
2. Material and Method
2.1. Experimental Setup
The experimental device used to investigate the propagation of gravity currents over the free surface of a miscible denser liquid at rest was designed and built in our laboratory, it comprises as shown in (Figure 1). A transparent basin made from Plexiglas, containing the static ambient liquid, of 700 L ( 300 cm long, 49 cm wide and 49 cm deep). A bowl of 240 L used to prepare the ambient fluid by introducing the quantity of salt corresponding to the concentration needed into a given volume of water. The solution prepared (salt water), then poured into the previous basin. A reservoir of 60 L equipped with a floodgate and which releases the gravity currents into the basin. An injection channel ( 600 mm long and 17 mm wide) manufactured in transparent glass and which links the reservoir to the basin. A light source made of 500 w (50 Hz) projector was placed ahead of basin to provide reflection of light source. The experiments were conducted in the dark laboratory room to a void other light sources disturbing the experiments.
2.2. Measurement Technique
A Techfluid 2150 flowmeter aiming at controlling and measuring the flow rate of the gravity current as it is released from the reservoir into an injection channel. The viscosity of the salty water was measured against the concentration using an Ostwald viscometer .The viscosity of the salty water increases with an increasing concentration in salt Cs (g/L). We note a good concordance between our results and the values of the viscosity of the seawater given by Weast [16] as shown in Table 1. Also the salinity of the salt water at the basin was measured using a calibrated conductivity meter, and it provides temperature measurements, which together with
![]()
Table 1. Dynamic viscosity of salty water in this work compared with those given by Weast using seawater [16] .
salinity.
An instrumentation equipment comprising: an observation system consisting of one SONY CCD XC-ST51/ ST51CE black and white camera equipped with a resolution of 768 × 576 pixels. The images observed by this camera is simultaneously captured at a frequency of 25 Hz or 50 Hz owing to a system of image capturing and which consists of a PC equipped with a Pentium IV processor (2.6 GHz) of 1024 Mb of random-access memory and provided with a Matrox Meteor II multi-voice at 8 bits smart card. Therefore, by using this card the images can be captured following 256 levels of grey.
2.3. Newtonian Gravity Currents Formation
The Newtonian gravity currents used in the experiments described are made of fresh water with density ρ-∆ρ in which a small quantity of Rhodamine B colouring agent as a tracer is introduced for video-photographic analysis purpose. Testing the density and the viscosity of these gravity currents, observed that the addition of Rhodamine B does not modify the physical properties of the gravity current. The ambient liquid at rest is salty water with adjustable density ρ by introducing an appropriate quantity of salt in a given quantity of water.
2.4. Experimental Procedure
A series of experiments were served in the dark room to identify gravity current flow properties, have been carried out. The measurement of the control parameters as Froude number is difficult because of the height of ambient fluid and mixing between dense and ambient fluids and variations in the velocity prevents the determination of local parameters only calculate initial Froude number 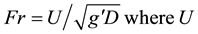 is the initial injection velocity, D is the diameter of channel, and
is the initial injection velocity, D is the diameter of channel, and  is the apparent acceleration of gravity at the injected source
is the apparent acceleration of gravity at the injected source 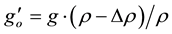 ranging from 0.36 to 2.6. The flow was laminar and then became a fully turbulent based on flow rate with channel Reynolds numbers
ranging from 0.36 to 2.6. The flow was laminar and then became a fully turbulent based on flow rate with channel Reynolds numbers 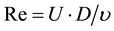 where υ is the kinematic viscosity in the range of 481 - 4434. The experimental procedure is discussed in the framework of Huppert theory [17] .
where υ is the kinematic viscosity in the range of 481 - 4434. The experimental procedure is discussed in the framework of Huppert theory [17] .
3. Velocity Field of Gravity Currents
3.1. Kinematic Field
A local characterization of the kinematic field, i.e. the local velocity and vorticity fields using the large scale PIV (LSPIV). The LSPIV technique is adapted for investigating a flow in large real configuration (rivers, dams, etc.) [4] [12] [15] . The measurement principle is based on Particle Image Velocimetry for large scale applications. The optical velocimetry technique uses conventional the digital imaging methods for the quantitative determination of two-component velocity data in a two-dimensional measurement plane [18] . The standard PIV method has been applied to velocity measurements at larger scales, commonly called large-scale particle image velocimetry (LSPIV) [11] [19] .
By the same way, we use the LSPIV technique which provides the reliable measurements of velocities with acceptable accuracy. In this case, the solid particles used in classical PIV are replaced by an inert colouring agent (e.g.: Rhodamine B), which is introduced in the gravity current injected in the ambient fluid. The images sequences recorded by the camera and then dissociated. The difference between the light intensities of the two liquids is observed on the images and their respective motions can be followed and analyzed using the time elapsed between two consecutive images. The laser beam used in classical PIV is replaced by a white light, as the contrast is perceptible to the naked eye. So the intensity differences caused by the intrusion level of the gravity current are observed. Table 2 provides a comparison between the two methods.
From one image to another one, by correlating the graphs, the displacement is determined. The use of the inter correlation algorithm to compute velocity (Figure 2 & Figure 3) and vorticity (Figure 3). Indeed, two images separated by a small time interval are selected using fenestration. Each window is analyzed: graphs representing the light intensity versus the position are derived. If necessary a modification of a correlation window is performed by redoing it with a smaller window.
3.2. Local Velocity and Vorticity
The local progress velocity is described by two components: U(x, y) and V(x, y) in the free surface. The (Figure 4) presents the axial velocity U(x, 0) and the lateral velocity V(x, 0). At fixed lateral direction (y = 0), the velocity of axial direction U(x, 0) (Figure 4(a)) is almost constant close to the injection channel, this can be explained by the presence of the inertia regime when the progress of front is linear with time. While far from the injection channel, the axial velocity decreases strongly with axial direction, this can be explained by the establishment of viscous regime. The lateral velocity V(x, 0) is very small in axial direction at y = 0 near the injection channel. While far from the injection, even the lateral velocity is small but it is of the same order than the axial velocity.
This can be explained that near the injection channel, the flow is one dimensional in x-direction where the vorticity is very small or vanishing (Figure 4(b)). Far from the injection channel, the free surface flow has two- dimensional propagation where the vorticity is not vanishing with a weak asymmetry with respect to the axis of the injection channel (Figure 4(b)).
Figure 5 presents the axial velocity U(0, y) and lateral V(0, y) at fixed axial direction (x = 0); the velocity of axial direction U(0, y) (Figure 5(a)) is maximal close to the injection channel and it decreases strongly with y. The lateral velocity V (0, y) vanishes at the injection channel and then it is maximal. The lateral velocity V(0, y) decreases strongly with y (Figure 5(b)).
![]()
Table 2. Comparison of classic PIV technique and large-scale PIV.
![]()
Figure 2. Spatio-temporal evolution of velocity for Cs = 10 g/Lang Fr = 0.71.
![]()
Figure 3. Spatio-temporal evolutions of velocity (left) and of vorticity (right) for Cs = 10 g/Lang Fr = 0.71.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Variation of the velocity with the axial direction at y = 0 of (a) axial component U(x,0) and of (b) lateral component V(x,0) for ∆ρ/ρ = 0.0196: Re = 3587: and Fr = 0.97.
4. Conclusions
An experimental investigation of the propagation of Newtonian gravity currents (colored fresh water) over the
free surface of a miscible denser liquid (salty water) at rest in a basin. Image processing technique has been proved for use in flow velocity measurement because of the initial evaluation of the feasibility of making flow surface measurements like in the natural waterways using video imagery determined the unique circumstances that will impact the quality of field video measurements. Our image processing software is based on the algorithm developed and is conceptually similar to the correlation imaging velocimetry [11] [20] . On the other hand, the Shallow flows are dominated by two-dimensional flow structures, which mean that the overall behavior of the flow can be analyzed using surface velocities. The characterization of flow was made by measurement of the velocity field and vorticity field using a large scale PIV technique. The application of Particle Image Velocimetry to measurement of velocity on large scales is a challenging necessity especially for investigation of injection gravity current propagation.
The image processing to estimate the surface velocity field with the LSPIV techniques, together of (corrected) images is processed to estimate surface velocity. Can be used as the natural light is used as illumination for LSPIV measurements instead of the laser light used in laboratory experiments that means no laser has to be used to provide fresh water at the basin, and using the free water surface as measurement gravity currents. Surface LSPIV measurements showed that the diffusion of dissolved tracer (Rhodamine B colouring) into the mixing
![]() (a)
(a)![]() (b)
(b)
Figure 5. Variation of the velocity with the axial direction at x = 0 of (a) axial component U(0,y) and of (b) lateral component V(0,y) for Cs = 10 g/L, and Fr = 0.71.
layer and the method involves surface velocity field injection estimation, and using initial flow parameters analysis as Froude Number.
Acknowledgements
This paper is part of the author’s PhD thesis in the field of Coastal Engineering at UBO (Université de Bretagne Occidentale).
NOTES
*Corresponding author.