Equivalent Risky Allocation: The New ERA of Risk Measurement for Heterogeneous Investors ()
1. Introduction
The Modern Portfolio Theory introduced by Markowitz [1] defines risk as the variance of portfolio return. Since its publication, many studies have shown that higher moments of the distribution of returns are relevant for asset allocation decisions [2] - [4] . Although several risk measures taking into account higher moments of asset returns’ distributions have been proposed in the literature (see for instance the paper of Coombs and Lehner [5] or Favre and Galeano [6] ), they do not take into account the investor’s “perception” of financial risks.
We define this notion of perception as the subjective judgment of an investor over the characteristics and severity of a potential loss. Undeniably, investors display heterogeneous attitudes towards the notion of “risk”. We can identify two extreme behaviors. Some investors put a very strong emphasis on the stability of returns around their mean and put a significantly less weight on extreme but rare losses. These are close to traditional “mean- variance investors”, in the scope of the Modern Portfolio Theory framework. At the other end of the spectrum, some investors primarily care about tail risk. They are sensitive to the threat of a shortfall with respect to a threshold level of wealth. These investors fall closer to the “mean-VaR (i.e., Value-at-Risk) investors” such as in the framework of Favre and Galeano [6] . Unfortunately, such a risk measure is inconsistent with any characterization of investor preferences under the Expected Utility Theory framework.
The objectives of our paper are twofold. We first aim to propose a risk measure derived from the Expected Utility Theory that explicitly takes into account the risk perception of the investor. This measure is applicable to various kinds of investor types, from one extreme to another. It is derived from Bell’s linear plus exponential (linex) utility function [7] , characterized by two parameters: one for the risk aversion, and one for the risk perception. The design of our risk measure, called Equivalent Risky Allocation (ERA), makes it practical, easily interpretable and comparable from one definition of risk to another. The ERA of a portfolio is the percentage invested in a specified benchmark (the rest being invested in the risk-free asset) that displays the same risk as this portfolio. This ERA has the advantage of providing a single and homogeneous value for the risk of each portfolio, while properly accounting for the heterogeneity of preferences among investors1. We demonstrate that for a same value of ERA, there exist several optimal portfolio allocations depending on the risk perception of the investor. Our second objective is to examine, with this new risk measure, the relevance of explicitly accounting for investors’ risk perceptions in their portfolio allocation decisions, both static and dynamic. Considering several investors with different risk profiles (risk perception and risk aversion) but confronted with the same set of asset classes and allocation constraints, we assess the consistency of using one-size-fits-it-all measures of risk, such as the variance or the value-at-risk (VaR), and compare the results with utility-based allocation schemes with the use of Bell’s measure.
We observe that, under a passive buy-and-hold strategy, the ERA obtained with Bell’s Risk Measure allows a better control of actual risk exposures than with the variance, which only addresses the stability of returns. Meanwhile, the VaR measure produces much more conservative allocations, at the expense of a lower variety of asset classes in the optimal allocations.
Under an active strategy with portfolio rebalancing every four weeks, applying the ERA with the proper risk perception enables the portfolio manager to tightly monitor and control her risk exposure. It is particularly relevant in the European MiFID directive context where taking account the proper risk perception of investors is one of the most valuable criteria. Portfolio risk, measured four weeks after the allocation, never moves further than 1% from its target. We also illustrate the influence of a different perception of risk on the allocations of the optimal portfolios. Finally, we show the impact of a wrong profiling through both an in-sample and out-of-sample check of the portfolio ERA measures with another risk profile than the one used for portfolio allocations. This acid test emphasizes the strong consistency of Bell [7] ’s risk measure and the quality of portfolios composed via this characterization of investor preferences. Such consistency is not warranted under the use of a measure of pure extreme risks, such as the VaR. Because the VaR is very sensitive to extreme events, the adoption of this measure for portfolio selection yields more instability over time. Bell’s utility function also accounts for tail risks, but in a more proportionate manner, which results in allocations whose consistency over time remains close to the ones of a mean-variance portfolio.
This paper is organized as follows. Section 2 introduces the two-dimensional framework with risk aversion and risk perception. In Section 3, we discuss the data and methodology for the empirical investigation of optimal allocations over time. All results are reported and analyzed in the fourth section. Section 5 discusses managerial implications, followed by the concluding section.
2. The Risk Aversion-Risk Perception Approach
2.1. Bell’s Risk Measure.
Bell [7] has proven that the only utility function compatible with a decision maker that prefers more money to less, wishes to obey the axioms of expected utility, is decreasingly risk averse at all wealth levels, wishes to obey the one-switch rule2 and will approach risk neutrality for small gambles when extremely rich, is the linex utility function:
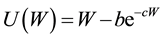 (1)
(1)
where W is the wealth level, b the risk aversion coefficient and c the risk perception coefficient. Both coefficients are positive and investor-specific.
Financial decision making under uncertainty is an issue of trading off risk against return. For that purpose, Bell [9] derives from his utility function an independent risk measure. His point is that the expected value of his utility function is a function of a measure of return, 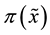 , a measure of risk,
, a measure of risk, 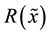 and of the initial wealth, W0. Writing the evaluation of an alternative as follows:
and of the initial wealth, W0. Writing the evaluation of an alternative as follows:
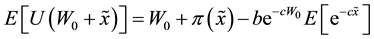 (2)
(2)
The only definition of risk compatible with Bell’s assumptions is the following:
 (3)
(3)
Because of parameter c which varies from one person to another, this measure is not unique but specific to each investor. The main advantage of this risk measure is that it includes, as special cases, many other measures of risk previously proposed in the literature.
Hlawitschka [10] demonstrates that the best quality of the approximation of Bell’s risk measure is achieved with the first fourth-order moments of the distribution. Consider the initial wealth of the investor W0 and the global amount invested in the risky asset I. The risk premium on this amount is equal to x = θ ? r, where θ is the return of the risky asset, and r is the risk-free return. The expected utility becomes:
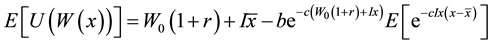 (5)
(5)
The Taylor series expansion of this expression around the mean is then:
 (6)
(6)
where 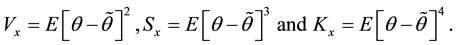 We refer to
We refer to 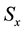 and
and 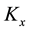 as the (un-standar- dized) skewness and kurtosis, respectively.
as the (un-standar- dized) skewness and kurtosis, respectively.
From this equation, we get the risk measure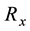 , for a standard unit of wealth:
, for a standard unit of wealth:
 (7)
(7)
An example is helpful in order to better understand the role of the risk perception parameter C. Suppose three different investors, respectively characterized by C equal to 5, 17 and 343. Each one is asked to choose between two assets characterized by the same expected return and the same variance (equal to 0.0029), but with different skewness and kurtosis. Table 1 provides the coefficient applied to the variance, skewness and kurtosis and their respective weights (between brackets) given by each investor. We can see from Table 1 that as C increases, more weight is put on the skewness and kurtosis.
![]()
Table 1. Illustration of the weight given to the 2nd, 3rd and 4th moment of the distribution in Bell Risk Measure for 3 different value of C, the risk perception parameter.
Comparing two assets with the same expected return and the same variance (and so the same risk in the mean-variance framework), but with different skewness and kurtosis, we can see the evolution of the risk measures (see Table 2). Whereas an investor using a traditional mean-variance approach will exhibit prefect indifference between both assets, the investor using the Bell Risk Measure will be more and more inclined to select Asset Y as her coefficient C gets bigger.
2.2. Equivalent Risky Allocation
In order to make the Bell Risk Measure easily interpretable and comparable, we propose to express this measure in terms of an Equivalent Risky Allocation (ERA). The ERA of a portfolio is the percentage invested in a specified benchmark (the rest being invested in the risk-free asset) that delivers the same risk as this portfolio. The benchmark can be any portfolio used as a reference, and is not constrained to be ex-ante or ex-post efficient. This makes our measure very simple and practical. In the mean-variance context, the ERA can be compared to a generalization of the weight put in a benchmark portfolio along the Capital Allocation Line4.
As the risk perception differs from one investor to another, there will be as many ERAs associated to a portfolio as the number of different investors. This measure provides a single index value for each portfolio, while properly accounting for the heterogeneity of the investors. The ERA can be applied to any measure of risk, as long as one uses the same measure to measure the risk of the studied asset and the risk of the benchmark. If the risk measure is homogeneous of degree 1 with the weight in the risky asset, such as the variance and the Bell Risk Measure, the formula of the ERA is:
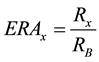 (8)
(8)
where RB is the risk value of the selected benchmark
To illustrate this measure, consider Asset X in the previous example. Take the S&P500 index as benchmark, and the variance as the risk measure. The monthly variance of the S&P500 is equal to 0.0023. The ERA is then:
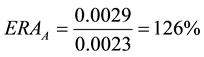
meaning that asset X is 26% riskier than the benchmark in terms of volatility, or that one needs to invest 126% of her wealth in the S&P500 (and borrow the 26% at the risk-free rate) in order to obtain the same risk level (measured by variance in this case) as her asset X.
This approach enables us to measure the risk of any portfolio with a single metric, irrespective of how the investor perceives the notion of risk. This is helpful in order to characterize the evolution of portfolios allocated with different risk-return optimization rules, as we do in the empirical section.
3. Data and Methodology
To compute optimal portfolios, we consider the weekly returns of nine equity indices and one bond index, for the period of January 7th, 2000 to November 5th, 2010. The equity indices are S&P500, S&P500 Growth, S&P500 Value, S&P400, S&P400 Growth, S&P400 Value, S&P600, S&P600 Growth and S&P600 Value total return indices. The bond index is JPM US Aggregate bond index total return.
![]()
Table 2. Illustration of the Bell Risk Measure’s value for two assets characterized by the same expected return and variance, but different skewness and kurtosis.
Table 3 displays the mean, minimum and maximum weekly returns of the 10 assets, over the whole period (564 weeks), as well as their standard deviation, skewness and kurtosis. The sample means of the series do not really reflect the return we can expect for their respective indices. The equity indices, being riskier than the bond index, display means lower than or close to the bond index and are even negative for S & P500 and S & P500 Growth. As we are primarily interested in the risk profile of the assets, we adjust the returns of the series using the Black and Litterman’s model [11] , smoothing the expected return through a market equilibrium model and combining our own view of the market returns with the equilibrium model’s returns. The main inputs of the Black-Litterman model are the “average” risk aversion, set to 2.5 by He and Litterman [12] , the variance-cova- riance matrix of the returns5, and the views we have of the market returns.
To specify our view, we go along with the Fama and French’s study [13] , showing that, on average, Growth companies have lower returns than Value companies, and that small companies have higher returns than larger ones. Using the Fama and French weekly factors average value over the preceding 78 weeks, we use an additional 0.11% weekly return for Value firms and for small companies. Moreover, we add the view that the bond index return must exceed the LIBOR 1M by its average spread for the last 18 months.
Table 4 displays our view of the returns of the equity indices, presented in matrix form. As requested by the Black-Litterman model, the sum of the weights given to the assets in a view is equal to 0 (resp. 1) when the view is relative (resp. absolute). The last line represents the vector of the adjustment to apply to the selected assets’ returns, expressed in weekly returns.
Table 5 shows the evolution of the posterior expected returns of the indices. We apply the model over a rolling window of 78 weeks over the entire sample period. The absolute value of the bond index presented in the table is its average value for the whole period.
Once the expected returns are smoothened with the Black-Litterman model, we construct defensive, median-risk and aggressive optimal portfolios, that is, with a maximum ERA of respectively 50%, 75% and 100%. The defensive (resp. median-risk, aggressive) portfolio is therefore constructed such as its risk is half (resp. 75%, 100% of) the risk of an equally weighted portfolio of the 9 equity indices (our benchmark)6.
We build these portfolios for four types of investor’s profiles:
- A “MVaR” investor, for whom we construct an optimal portfolio maximizing her expected return for a given Modified Value-at-Risk7;
- A protective investor, more affected by extreme losses than variability. Her portfolio is constructed using the Bell risk measure with a high C, equal to 34;
- A stable investor, more affected by variability than extreme events, characterized by a low C, equal to 5;
- A Markowitz investor, for whom we construct an optimal portfolio maximizing his expected return for a given variance.
4. Results
In order to compare our twelve optimal portfolios computed with 4 different risk measures for three levels of risk, the risk values are systematically expressed in ERA. In the first sub-section we test the time consistency of the Bell Measure for a fixed-weights portfolio, by observing the evolution of the ERA over time. Then, we test the time consistency of the measure for a rebalanced portfolio. Finally, we test the portfolio consistency by recomputing the risk measures for the rebuilt historical of the rebalanced portfolios. Note that all portfolios are constructed under the constraint that the maximum weight of each equity index is set to 20%.
![]()
Table 3. Descriptive statistics of the weekly returns’ distributions of the indices.
![]()
Table 4. Inputs of the Black-Litterman model: types of views and estimated returns.
![]()
Table 5. Average expected returns of the equity indices before, during and after the implementation of the Black-Litterman approach.
4.1. Time Consistency with No Rebalancing
In order to test the coherence of the risk measure over time, we construct 12 optimal portfolios, i.e., for 3 levels of risk and for 4 different perceptions of risk, every 4 weeks, starting on June 29th, 2001, until November 5th, 2010, and we observe the evolution of their ERA.
Table 6 presents the average optimal allocations for the 12 optimal portfolios and compares their ERA on the day of the optimization for the 4 investors. The ERA is highlighted when the correct risk measure is used for the specified investor. Using the wrong risk measure for the investors can make them bear a too high risk level or miss a higher expected return by reducing too much the risk taken. Indeed, for defensive and median-risk portfolios, if we use a Bell Risk Measure with a high C (34), the optimal portfolios are too risky for the other investors, as their ERA are higher than the required value (50% and 75%). On the other hand, investors, for whom we have computed an optimal portfolio using erroneously the MVaR, have a portfolio with too little risk, with a potential loss in expected return.
The observation of these average values already hints over the complexity induced by the various notions of risk perceived by the investors. Indeed, a protective investor is not always the one with the highest allocation in bonds. Taking a look at the average allocations of the portfolios (right part of Table 6), we can see that for an analogous amount of risk, the allocations differ quite significantly from one another. The MVaR portfolios differ the most from the other ones, as they are usually composed of much more bonds than with the other risk measures. For a low level of risk, a MVaR investor will invest, on average, 51% in the bond index, whereas the other investors will have, on average, less than 30% invested in the bond index. This difference is not as significant for aggressive portfolios.
The last column of Table 6 reports the standard deviation of portfolio weights. The optimal allocations for investors using Bell risk measure are more stable than using variance of MVaR. The allocations obtained with these two classical risk measures are twice as volatile as the ones produced with Bell’s measures.
![]()
Table 6. Average equivalent risky allocation of optimal portfolios for 4 different investors and average allocations of these portfolios.
The portfolios are optimized every 4 weeks on the basis of the preceding 78 weekly returns (from June 29th, 2001 to November 5th, 2010) of 10 indices, with 4 different risk measures. The indices are S&P500, S&P500 Growth, S&P500 Value, S&P400, S&P400 Growth, S&P400 Value, S&P600, S&P600 Growth, S&P600 Value and JPM US Corp Bond index. The risk measures are the variance, the Bell’s Risk Measure (Bell) with a perception parameter C equal to 5, and equal to 34, and the Modified Value-at-Risk with a 97.5% level of confidence. Under each risk measure, we construct three portfolios: a defensive (ERA = 50%), a median-risk (ERA = 75%) and an aggressive (ERA = 100%) portfolio. The ERA is the value of the risk measure of the optimal portfolio, divided by the value of the same risk measure for the benchmark. The benchmark chosen is an equally weighted portfolio of the 9 equity indices.
We then analyze the evolution of the ERA of each portfolio over time. Each portfolio’s ERA is computed every week after the optimization until 3 years later. The procedure is reproduced over a rolling window of 18 months. Figure 1 displays, for the medium-risk portfolios8, the evolution of the averages, the 5% and 95% quantiles of these ERAs, according to the number of weeks elapsed since the allocation date. The dashed lines represent the target value of the portfolios optimizations (75% in this example).
The value taken by the ERAs after three years is on average equal to respectively 82%, 85%, 88% and 92% for resp. the MVaR, BellC=34, BellC=5 and variance, which means that the portfolios optimized with the traditional variance approach are the least likely to remain close to their risk target.
4.2. Time Consistency with Rebalancing.
Although it provides informative outputs, the previous exercise is not very close to the reality of asset managers. Hence, in the following application, we do not consider the different allocations of each investor separately, but we study the dynamics of the 12 portfolios reallocated every four weeks. Figure 2 (resp. 3 and 4) displays the evolution of the weights of the 10 indices for the defensive portfolios (resp. median risk and aggressive) constructed for the 4 different perceptions of risk considered (Figure 3).
Next, we study the evolution of the risk taken by the investors through time. Table 7 and Table 8 compare the ERA of the actively managed portfolios for the 4 investors. They report the average ERA on the day of the allocation (ERAt) and the average ERA four weeks later, just before the next allocation (ERAt+4). The average differences between both ERA (bias) and the Root Mean Square Errors (RMSE), expressed in percentage of the ERAt, are also reported. The shaded sections highlight the measures when the right method is used for the right investor. Table 7 (resp. 8) displays those results for the defensive (resp. median-risk) portfolios. The defensive
![]()
Figure 1. ERA quantiles of meadian-risk portfolios for 4 different investors.
MVaR investor Protective investor
![]()
![]()
Table 7. Equivalent risky allocation for defensive investors.
Average Equivalent Risky Allocation of 4 portfolios rebalanced every 4 weeks on the day of the allocation, ERAt, and 4 weeks after, just before the next allocation (ERAt+4), for 4 different investors (Markowitz, Stable, Protector and MVaR). The portfolios are optimal portfolios under the constraint that the ERA is set to 50% for 4 different risk measures (variance, Bell’s Risk Measure with perception parameter C = 5 and 34 and MVaR). The bias and root mean squared errors (RMSE) are computed as a percentage of the average of ERAt.
![]()
Table 8. Equivalent risky allocation for median-risk investors.
Average Equivalent Risky Allocation of 4 portfolios rebalanced every 4 weeks on the day of the allocation, ERAt, and 4 weeks after, just before the next allocation (ERAt+4), for 4 different investors (Markowitz, Stable, Protector and MVaR). The portfolios are optimal portfolios under the constraint that the ERA is set to 75% for 4 different risk measures (variance, Bell’s Risk Measure with perception parameter C = 5 and 34 and MVaR). The bias and root mean squared errors (RMSE) are computed as a percentage of the average of ERAt.
MVaR investor Protective investor
and median-risk portfolios of the protective investors tend to be perceived as riskier than expected by the other investors.
The portfolios of the MVaR investors look less risky than targeted for the other investors. Thus even if the MVaR measure seems more stable in a passive strategy, this measure is totally inaccurate for investors using variance or Bell Risk Measure to take their decisions.
The bias levels show that the allocation processes perform well in regards to their objective, as all biases are lower than 1%, except for the Bell34 investor where a wrong measure can reach a 3.6% bias. It nonetheless does not outreach the 1.1% threshold when the correct measure is used.
If we look at the RSME, we clearly see that, if one does not know the investor’s profile, the MVaR risk measure is most likely to be misleading. It can produce ERA more than 20% far away from its objective. This tends to improve for higher degree of risk. For the Bell Risk Measure, even if one misestimates the perception parameter, the highest RMSE is half the MVaR’s, and the method even improves comparatively when the level of risk rises, with a RMSE of maximum 6.3% for an ERA of 100%.
4.3. Portfolio Consistency.
After having checked for the time consistency of the risk measure, an ex-post validation is necessary. The investor must be able to verify afterwards whether the portfolio held during the whole investment horizon has realized its objectives in term of risk.
To test the portfolio consistency of our 12 portfolios, we rebuild the historical of the rebalanced portfolios and compute their ERA on the last day of the holding period, that is, on November 5th, 2010. Table 9 displays the final ERAs of the 12 portfolios, constructed on June 29th, 2001, and rebalanced every four weeks until October 15th, 2010. The last column displays the maximum spread between the ERA of the investor for whom the risk measure used for the optimization is the right one (in bold), and the ERA of the others investors.
Results in Table 9 indicate that the portfolios created and periodically rebalanced for the different investors (in bold) have been riskier than expected, except for the Markowitz-median risk investor and the MVaR-ag- gressive one. Whereas the portfolios were reallocated every four weeks, with the constraint that the ERA must be lower than 50%, 75% and 100%, the final ERAs are higher than the target values. This is partially due to an increase of the global risk of the “return drivers”. Indeed, the variance (resp. kurtosis) of the S&P600 Value index has, for instance, increased from 52% to 225% (resp. from 18% to 568%) of the benchmark variance (resp. kurtosis). The MVaR is the least reliable method, even if used for the correct investor.
The relative increase of the ERA is lower, the higher the expected ERA. This might be due to the S&P600 index and, to a smaller extent, to S&P500 and 400 indices, which have experienced a reduction in variance and kurtosis over the tested period. The spread between the ERAs of different investor types for a same portfolio
![]()
Table 9. Final equivalent risky allocation of 12 rebalanced portfolios for 4 different investors (Markowitz, Protective, Stable, MVaR).
Equivalent Risky Allocation of 12 portfolios rebalanced every 4 weeks, for 4 different investors (Markowitz, Stable, Protector and MVaR). The portfolios are optimized every 4 weeks on the basis of the preceding 78 weekly returns (from June 29th, 2001 to November 5th, 2010) of 10 indices, with 4 different risk measures. The indices are S&P500, S&P500 Growth, S&P500 Value, S&P400, S&P400 Growth, S&P400 Value, S&P600, S&P600 Growth, S&P600 Value and JPM US Corp Bond index. The risk measures are the variance, the Bell’s Risk Measure (Bell) with a perception parameter C equal to 5, and equal to 34, and the Modified Value-at-Risk with a 97.5% level of confidence. Under each risk measure, we construct three portfolios: a defensive (ERA = 50%), a median-risk (ERA = 75%) and an aggressive (ERA = 100%) portfolio. The ERA is the value of the risk measure of the optimal portfolio, divided by the value of the same risk measure for the benchmark. The benchmark chosen is an equally weighted portfolio of the 9 equity indices.
illustrates the consequence of a wrong profiling. A misunderstanding of the investor’s perception of risk could make her endure a risk up to 45% away from her objective. Besides, using the wrong risk measure for an investor appears to be more damageable for defensive portfolios, as the maximum spread is higher for those portfolios.
5. Implications for Portfolio Management
Our framework happens to yield significant implications for portfolio management at three levels: i) by introducing an operationally affordable tool to account for risk perception in investor profiling; ii) by showing how actual portfolio allocations are sensitive to the proper adequacy between asset return properties and two-di- mensional investor profiles; iii) by summarizing the risk measure in an intuitive and easily interpretable fashion which is especially relevant in the European MiFID regulations context.
On the one hand, the traditional notion of risk aversion refers to the rational expected utility theory. On the other hand, the dimension of risk perception, which involves a personal assessment of the nature of risk, more closely relates to behavioral finance. Thanks to the linex utility function, these two dimensions are reconciled in a single framework that summarizes the investor with two parameters. Unlike Kahneman and Tversky’s prospect theory [15] , the use of Bell’s utility function does not leave the paradigm of a uniquely defined, increasing, continuous and differentiable utility function. For the practical purpose of measuring investors’ profiles and applying consistent and adequate portfolio recommendations, the adoption of the linex function instead of, for instance, the negative exponential or the power utility function (as in Morningstar’s MRAR methodology, for instance) only requires the estimation of a second parameter. This means that any investment advisor’s profiling system has to be adapted, not replaced in order to comply with this more sophisticated approach of measuring preferences over risk and return. From an organizational perspective, this potentially makes a huge difference.
Does the explicit account for risk perception really lead to improving the quality of portfolio advice and the outcomes of the asset allocation process? Our tests clearly show that, even for relatively homogenous equity investments, an inadequate investor profile that ignores the heterogeneity of investors regarding their risk perception is likely to lead to significant errors, both in static allocations and in dynamic portfolio properties. The attribution of “one-type-fits-it-all” portfolios optimized with the wrong underlying utility function yields potential investor dissatisfaction because the portfolio behavior does not correspond to her profile. Furthermore, the dynamic properties of such misspecified portfolios induce a risk drifting that aggravates the initial mistake. Ignoring risk perception, while this is a major determinant of an investor’s attitudes towards risk, has considerable implications in expected utility maximization.
Finally, the introduction of ERA as a way to express risk extends its applicability beyond the use of Bell’s risk measure, but is particularly suitable in this context. It meets the challenge of expressing the risk of a financial instrument when this risk is not homogeneously perceived by investors. Our original framework has addressed several important issues in risk perception analysis and delivers in the end several meaningful insights for either practitioners or national and international regulatory authorities.
6. Conclusions
This study has demonstrated the relevance of the perception of risk, defined as the subjective judgment of an investor about the characteristics and severity of a risk, for portfolio allocation. Although confirmed several times in experimental finance (see [16] and [17] among others), none of the authors were able to reconcile their perception driven risk measure with the theory of utility function until the advent of Bell’s contribution [18] . He derives a risk measure from a linex utility function and approximates the risk perception of the investor through an individualized specific parameter.
The Bell Risk Measure allows us to adequately address the request of an increasing number of researchers and practitioners advocating for the introduction of higher moments of the distribution of returns when optimizing portfolios. For that purpose, we also compare our results with an optimization using MVaR, another risk measure taking into account higher moments of distribution.
The risk measure retrieved from the linex function is much more complicated to interpret than the mere variance or a VaR. As a first contribution, we have proposed a standardization technique that simplifies its interpretation but keeps its individualization specificity: the Equivalent Risky Allocation (ERA). This measure simply expresses the risk measure of an asset in terms of a percentage of the wealth to invest in a selected benchmark to obtain the same risk value.
Through an application of portfolio optimization using nine equity indices and a bond index, we test the time and portfolio consistency of the measure and compare it with the variance of Markowitz and the MVaR which we also express in terms of ERA. Although the variance is a particular case of the Bell Risk Measure with its risk perception C that tends to zero, our research shows the relevance of the recognition of the risk perception in portfolio allocation. Moreover, we demonstrate the consequences of a misspecification of the risk profiles of the investors who are brought to encounter a too high risk or to miss potentially higher returns. Finally, we demonstrate the weakness of MVaR which tends to produce too defensive portfolios for investors using other risk measure as reference.
The limit of this study remains, as in all quantitative approaches, in the need of sufficient historical data. Introducing non classical assets in the portfolio, such as structured products or derivative products, would require using additional techniques in order to “translate” those assets into time series. This methodology also could be tested on larger portfolios and other time periods. Finally, whereas the authors have shown the consequences of a wrong risk profile, the value of the risk perception C of the utility function may be difficult to parametrize.
Acknowledgements
This paper has benefitted from comments by Yves Crama, André Farber, Olesya Grishchenko, Olivier Lecourtois, Aline Muller and François Quittard-Pinon, as well as EM Lyon seminar participants and the 2010 French Finance Association Conference (St-Malo) attendees. We thank Laurent Bodson and Gaël Minon for research support. Georges Hübner acknowledges financial support from Deloitte. Séverine Plunus acknowledges financial support from KBL Private Bankers.
NOTES
*Corresponding author.
![]()
1This desirable property is not shared by the framework introduced in Zakamouline and Koekebakker [8] who propose a performance measure including higher moments of distribution derived from the hyperbolic absolute risk aversion (HARA) utility function. Their measure requires the assumption that all investors share the same perception of risk.
![]()
2“A decision maker obeys the one-switch rule if, for every pair of alternatives whose ranking is not independent of wealth level, there exists a wealth level above which one alternative is preferred, below which the other is preferred” [1] .
3As Bell does not propose any value for C, we derive its highest value empirically, by constructing optimal portfolios on the basis of four assets: a risk-free one, a low-variance-high kurtosis one, a high-variance-low kurtosis one and a high-variance-high kurtosis one. After setting the weights of the risk-free and the high-risk assets equal, the C producing the portfolio with the highest weight in the high-variance was equal to 34, and the C producing the portfolio with the highest weight in the high-kurtosis asset was equal to 5.
![]()
4It is not necessary to constrain the benchmark to be the market portfolio. Be it the case, the Capital Allocation Line becomes the Capital Market Line.
![]()
5We use an estimation window of 18 months.
6We have tested different benchmark specifications but all results remain qualitatively robust.
7We used a 97.5% confidence level as suggested in Canevaile and Lejeune [14] .
![]()
8The trends and conclusions are the same for the defensive and aggressive portfolios.