1. Introduction
The classical Cramer-Lundberg risk model assumes that the stochastic process 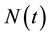 denotes the number of claims up to time t and the random variables Xj, the claim size of the j-th claim. In this model,
denotes the number of claims up to time t and the random variables Xj, the claim size of the j-th claim. In this model, 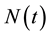 is independent of the claim sizes and the claim sizes are independent and identically distributed; however, this assumption is too restrictive at times. Several authors have proposed models with dependence between the risks. Among the various types of dependence models proposed, in this paper we refer to the case where the dependency is obtained assuming that the insurer has
is independent of the claim sizes and the claim sizes are independent and identically distributed; however, this assumption is too restrictive at times. Several authors have proposed models with dependence between the risks. Among the various types of dependence models proposed, in this paper we refer to the case where the dependency is obtained assuming that the insurer has 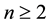 correlated classes of insurance business, where
correlated classes of insurance business, where  is the number of claims of the i-th class;
is the number of claims of the i-th class;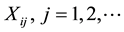 , is the claim sizes of the j-th claim of the i-th class and the numbers
, is the claim sizes of the j-th claim of the i-th class and the numbers 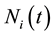 are dependent claim count processes. Models of this type are proposed in [1] -[6] . In [3] [4] , a risk model involving two dependent classes of insurance business is considered in a given period of time and the expected utility of the insurer wealth is maximized by the determination of optimal retention limits of Unlimited or Limited Excess of Loss reinsurance.
are dependent claim count processes. Models of this type are proposed in [1] -[6] . In [3] [4] , a risk model involving two dependent classes of insurance business is considered in a given period of time and the expected utility of the insurer wealth is maximized by the determination of optimal retention limits of Unlimited or Limited Excess of Loss reinsurance.
In this paper, we consider an optimal proportional reinsurance problem of an insurer whose surplus process is generated by two dependent classes of insurance business. The objective is to choose an optimal reinsurance strategy; in order to maximize the insurer’s expected exponential utility of terminal wealth we use the dynamic programming approach.
The paper is organized as follows. In Section 2, we present the risk model. In Section 3, we find the surplus evolution and the conditional expected utility of the insurer’s terminal surplus, define the problem and give the corresponding value function. In Section 4, using the infinitesimal generator, we derive the HJB equation and justify the form of the value function. Finally, in Section 5, we discuss the solution giving an explicit solution in a particular framework.
2. The Model
In the finite time horizon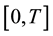 ,
, 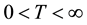 , we consider a model that involves two risks that may represent two classes of insurance business dependent through the number of claims. Let
, we consider a model that involves two risks that may represent two classes of insurance business dependent through the number of claims. Let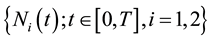 , are the arrival processes of the respective claims. We denote by
, are the arrival processes of the respective claims. We denote by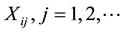 , the random variable claim size of the risk i, i = 1, 2, assuming that these random variables have respectively the same distribution function Fi, with
, the random variable claim size of the risk i, i = 1, 2, assuming that these random variables have respectively the same distribution function Fi, with 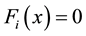 for
for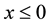 , and mean values
, and mean values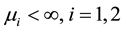 . Moreover, we assume that the moment generating function of the random variables
. Moreover, we assume that the moment generating function of the random variables 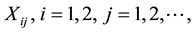 exists. Finally, we assume that the random variables
exists. Finally, we assume that the random variables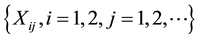 , are mutually independent, and independent of
, are mutually independent, and independent of . We denote by
. We denote by![]() ,
, ![]() , the aggregate claims amounts of the risk i, i = 1, 2. We assume that the processes
, the aggregate claims amounts of the risk i, i = 1, 2. We assume that the processes![]() , are Poisson processes defined as follows:
, are Poisson processes defined as follows:
![]() (1)
(1)
where ![]() are Poisson random variables that are mutually independent having positive mean, in the time unit,
are Poisson random variables that are mutually independent having positive mean, in the time unit, ![]() respectively. It follows that
respectively. It follows that ![]() has a Poisson bivariate distribution and that
has a Poisson bivariate distribution and that ![]() and
and ![]() are correlated by
are correlated by![]() ; in fact, it results:
; in fact, it results:
![]() (2)
(2)
In the following, we will use the variables Xi, i = 1, 2, identically distributed to ![]()
We denote by c, i = 1, 2 the premium rate, for the time unit, assuming that the premium calculation principle is the expected value principle with loading coefficient![]() , that is:
, that is:
![]() (3)
(3)
We introduce a proportional reinsurance: the reinsurer pays![]() ,
, ![]() , of each claim of the type i, i = 1, 2 and he receives from the insurer the reinsurance premium. We denote by
, of each claim of the type i, i = 1, 2 and he receives from the insurer the reinsurance premium. We denote by![]() , i = 1, 2, the reinsurance premium and we get
, i = 1, 2, the reinsurance premium and we get
![]()
for which it is
![]() (4)
(4)
Note that the condition ![]() linked to the positivity of the security loading is not assumed, as it may or may not be satisfied.
linked to the positivity of the security loading is not assumed, as it may or may not be satisfied.
3. The Problem
We denote by ![]() the proportion insured at time t,
the proportion insured at time t, ![]() , where
, where ![]() is therefore the risk exposure of insurer at time t. We assume that, at every time t,
is therefore the risk exposure of insurer at time t. We assume that, at every time t, ![]() , the insurer can choose the risk exposure
, the insurer can choose the risk exposure![]() , according to the observable information about the insurance risk processes up to time t. There- fore
, according to the observable information about the insurance risk processes up to time t. There- fore![]() , i = 1, 2, are the insurer’s control parameters; let
, i = 1, 2, are the insurer’s control parameters; let ![]() be the set of all admissible policies. The objective for the insurer is to choose an optimal reinsurance strategy that maximize the expected exponential utility of terminal wealth. We will make use of the HJB theory to face the problem. After the reinsurance the total claim amount charged to the insurer is
be the set of all admissible policies. The objective for the insurer is to choose an optimal reinsurance strategy that maximize the expected exponential utility of terminal wealth. We will make use of the HJB theory to face the problem. After the reinsurance the total claim amount charged to the insurer is
![]() (5)
(5)
We denote by ![]() the surplus process of the insurer adopting the reinsurance strategy process
the surplus process of the insurer adopting the reinsurance strategy process![]() . The surplus evolves over time as:
. The surplus evolves over time as:
![]() (6)
(6)
We recall that ![]() and
and ![]() are defined by (1), then the process
are defined by (1), then the process ![]() has a bivariate Poisson distribution. This fact, noting that the process has stationary increments (see [7] ) and using results in [8] , allows us to determine the following joint probabilities:
has a bivariate Poisson distribution. This fact, noting that the process has stationary increments (see [7] ) and using results in [8] , allows us to determine the following joint probabilities:
![]()
![]()
![]()
![]()
From previous result it follows
![]() (7)
(7)
where Xi are identically distributed to Xij,![]() .
.
We consider an utility function![]() ,
, ![]() , strictly increasing and concave (that is
, strictly increasing and concave (that is ![]() and
and![]() ). For each control strategy
). For each control strategy![]() ,
, ![]() , given
, given![]() ,
, ![]() , we define the following conditional expected utility of the insurer’s terminal surplus:
, we define the following conditional expected utility of the insurer’s terminal surplus:
![]() (8)
(8)
As previously stated, the insurer’s goal is to determine an optimal reinsurance strategy ![]() so as to maximize the expected utility of the terminal surplus (8). We therefore consider the following problem
so as to maximize the expected utility of the terminal surplus (8). We therefore consider the following problem
![]() (9)
(9)
It follows that the insurer has to find the optimal strategy ![]() and the corresponding value function
and the corresponding value function ![]() such that:
such that:
![]() (10)
(10)
with the usual boundary condition (see [9] [10] )
![]() (11)
(11)
4. The HJB Equation and the Value Function
We can find the infinitesimal generator for the process ![]() and for the function V. The procedure is similar to that one used in [11] and in [12] .
and for the function V. The procedure is similar to that one used in [11] and in [12] .
Theorem 1. Let ![]() be defined by (9) and (10) and let
be defined by (9) and (10) and let![]() . Therefore, V satisfies the following HJB equation:
. Therefore, V satisfies the following HJB equation:
![]() (12)
(12)
Proof. We derive the following infinitesimal generator for the process ![]() and for the function V:
and for the function V:
![]() (13)
(13)
it allows us to write the HJB Equation (12).
We recall that, by (6) and (7) it results in
![]()
therefore we have, remembering the independence between Xi and Ni, i = 1, 2:
![]()
Therefore V must satisfy Equation (12). ■
We introduce the following utility function
![]() (14)
(14)
With the purpose to write (9) we observe that:
1) from (6) and remembering that Poisson processes have stationary increments, we obtain:
![]() (15)
(15)
with, as previously stated,![]() ;
;
2) in Section 2 we have assumed that the moment generating functions of random variables![]() ,
,![]() , and therefore of random variables
, and therefore of random variables![]() ,
, ![]() exist.
exist.
We denote those functions by![]() ,
, ![]() and we observe that
and we observe that![]() ;
;
3) according to [7] and from the probability generating function of the bivariate Poisson distribution (see [8] , p. 126), it results in:
![]() (16)
(16)
4) from the previous considerations, we have:
![]() (17)
(17)
Because of these considerations, we assume that the value function V, defined by (10) with the condition (11) has the form
![]() (18)
(18)
with the condition
![]() (19)
(19)
5. Possible Solutions
We consider the assumptions (18); it results in:
![]()
![]()
![]()
Therefore, (12) becomes
![]()
with![]() ; hence, remembering that
; hence, remembering that![]() , it results in:
, it results in:
![]() (20)
(20)
with![]() .
.
Assuming the particular case where the insurer’s risk exposure is the same for the two classes of the insurance business; that is ![]() the control parameter is
the control parameter is ![]() (resulting in
(resulting in![]() ), and (20) becomes:
), and (20) becomes:
![]() (21)
(21)
with![]() . The problem of the determination of the optimal control
. The problem of the determination of the optimal control ![]() can be easily solved, as we will see in the following.
can be easily solved, as we will see in the following.
For simplicity, we write (21) as follows
![]()
observing that
![]() (22)
(22)
from which we obtain:
1) ![]() by (3) and (4), from which we deduce that
by (3) and (4), from which we deduce that ![]() is an increasing function in
is an increasing function in ![]() and therefore
and therefore![]() ;
;
2) ![]()
![]() ;
;
3) ![]()
From the previous results it follows that ![]() is equal to zero in a single point
is equal to zero in a single point ![]() and:
and:
if ![]() and therefore
and therefore![]() ;
;
if ![]() and therefore
and therefore![]() ;
;
if ![]() and therefore
and therefore ![]()
being
![]() (23)
(23)
We therefore obtain the following results.
If ![]() it results in
it results in ![]() and by (21) we have:
and by (21) we have:
![]()
with![]() , from which we obtain
, from which we obtain
![]() (24)
(24)
then the resulting value function (18) is:
![]()
If ![]() it results in
it results in ![]() such that
such that![]() . Therefore, remembering (22), it results in
. Therefore, remembering (22), it results in
![]() (25)
(25)
and by (21):
![]()
with![]() . From the previous, with a procedure analogous to that followed in the case
. From the previous, with a procedure analogous to that followed in the case![]() , it is possible to find
, it is possible to find ![]() and the resulting value function.
and the resulting value function.
Acknowledgements
We thank the Editor and the Referees for their comments.