Order Degree Evaluation of Information System Based on Improved Structural Entropy ()
1. Introduction
Information systems, as heterogeneous complex systems, show differences in many aspects such as computer software, hardware and information resource management [1] [2] . Thus, interactions between subsystems are heterogeneous, which means that information flow in information system is directed. Under increasingly complex environment, interactive directions between subsystems are more significant. Directions of information exchange, an inner mechanism for information systems to output information, influence the stability and order degree of systems to a large extent. It is necessary to evaluate order degree of information systems under the internal mechanism so that enterprises can assess order degree of their information system more accurately, which plays a vital role in the stable operation of information systems.
Currently, there exist two major methods to compute order degree of systems: 1) multiple independent order parameters are selected to determine multi-dimensional order degree at the macro level [3] ; 2) at the micro level, system entropy is measured to reflect order degree [4] . The paper studies how directed information flow between subsystems affects order degree of systems; entropy is thus applied to evaluate order degree of systems. For generalized information systems, entropy can be used to measure disorder degree of systems. High entropy denotes that information system cannot obtain or utilize information effectively, which results in a huge loss of information in information systems. Entropy has been widely used to evaluate order degree of various systems or organizational structures. Shannon [5] first proposes quantitative information entropy to measure order degree of systems. Literature [6] [7] homogenizes information and resource flow and then puts forward structural entropy to measure order degree of organizational structure. Structural entropy is also used to evaluate order degree of cellular manufacturing systems and manufacturing resource organization modes [8] [9] . Furthermore, structural entropy can be applied to many other systems such as supply chain system and biological system [10] [11] .
Literature above is based on homogeneous interactions between subsystems which are heterogeneous in reality. For example, information flow is directed in information systems. Our work builds on this literature and extends structural entropy to incorporate directed information flow required to evaluate order degree of information systems. Finally, a case study is given to test the method.
2. Analysis of Original Structural Entropy Model
Literature [6] presents structural entropy model to evaluate order degree of system structure shown in Figure 1(a). The structure entropy model is briefly introduced as follows. In Figure 1(a), the set of system elements is 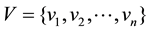 where vi (1 ≤ i ≤ n) is a subsystem. Let L(vi, vj) denotes the length of shortest path between subsystems vi and vj. If vi and vj are directly connected, L(vi, vj) = 1. Otherwise, let L(vi, vj) increase by one for each transfer. W(vi) is the number of the subsystems that directly linked with vi. According to the definition of information entropy, the probability of time effect microscopic state between vi and vj is denoted as
where vi (1 ≤ i ≤ n) is a subsystem. Let L(vi, vj) denotes the length of shortest path between subsystems vi and vj. If vi and vj are directly connected, L(vi, vj) = 1. Otherwise, let L(vi, vj) increase by one for each transfer. W(vi) is the number of the subsystems that directly linked with vi. According to the definition of information entropy, the probability of time effect microscopic state between vi and vj is denoted as
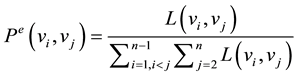 (1)
(1)
and the time effect entropy between vi and vj is
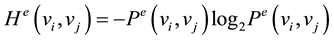 . (2)
. (2)
The total time effect entropy is summed as
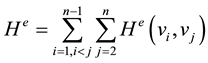 , (3)
, (3)
and the biggest time effect entropy is
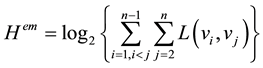 . (4)
. (4)
Finally, the time effect order degree of the system is
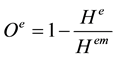 . (5)
. (5)
Moreover, the probability of quality microscopic state of subsystem vi is define to be
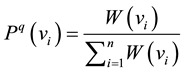 , (6)
, (6)
and the quality entropy of vi is
![]() (a) (b)
(a) (b)
Figure 1. (a) System structure neglects directed information flow; (b) System structure incorporates directed information flow.
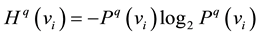 . (7)
. (7)
The total quality entropy is summed as
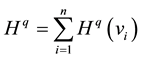 , (8)
, (8)
and the biggest quality entropy is
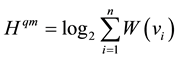 . (9)
. (9)
Finally, the quality order degree of the system is
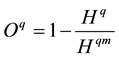 . (10)
. (10)
Thus, order degree of the system is synthesized as
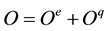 . (11)
. (11)
From the above expressions, we can find that: 1) the computation of time effect entropy regards the information flow between two arbitrary subsystems non-directional, but information flow between subsystems is designed to be directed in reality to ensure the timeliness of information; 2) the calculation of quality entropy considers that all subsystems correlated with vi influence the information quality of vi, but in reality information quality of subsystem vi is only affected by its direct upstream systems. The fundamental reason of the above two problems is that directions of information flow are neglected. Thus, the algorithms of L(vi, vj) and W(vi) need to be revised. Order degree evaluation, which takes directions of information flow into account, is more in line with the actual structure of information system.
3. Improved Structural Entropy Model
Based on previous research on structural entropy and order degree, the paper proposes improved structural entropy to evaluate order degree of information system. The real-world structure of information system is shown as Figure 1(b). The set of information subsystems is marked as 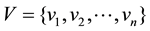 where vi represents a subsystem. There is an edge eij between vi and vj if information passes from vi to vj, and viand vj respectively stand for the start and end of edge eij. There exist two edges eij and eji if information flow is bidirectional. The in-degree of vi is computed as the number of upstream systems of vi, denoted as d−(vi). The path that information passes from vi to vjis denoted by
where vi represents a subsystem. There is an edge eij between vi and vj if information passes from vi to vj, and viand vj respectively stand for the start and end of edge eij. There exist two edges eij and eji if information flow is bidirectional. The in-degree of vi is computed as the number of upstream systems of vi, denoted as d−(vi). The path that information passes from vi to vjis denoted by 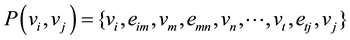 where vertexes and edges are non-redundant. The number of edges in P(vi, vj) represents length of the path, and length of the shortest path from vi to vj is denoted by L(vi, vj). L(vi, vj) may not be equal to L(vj, vi) for directed information flow between subsystems.
where vertexes and edges are non-redundant. The number of edges in P(vi, vj) represents length of the path, and length of the shortest path from vi to vj is denoted by L(vi, vj). L(vi, vj) may not be equal to L(vj, vi) for directed information flow between subsystems.
Improved structural entropy model measures order degree of information system through time effect entropy and quality entropy which separately reflect level of timeliness and accuracy of information. Specifically, improved time effect entropy redefines time effect microscopic state between subsystems while improved quality entropy revises quality microscopic state of each subsystem.
3.1. Improved Time Effect Entropy Model
The probability of correlated time effect microscopic state from vi to vj is denoted as
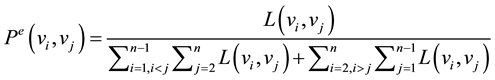 , (12)
, (12)
where ![]() represents the total time effect microscopic state and L
represents the total time effect microscopic state and L
(vi, vj) denotes the time effect microscopic state from vi to vj. The shortest path from vi to vj may differ from the shortest path from vj to vi. Thus, distinguishing time effect microscopic state and its probability between vi and vj is necessary.
The time effect entropy from vi to vj is
![]() , (13)
, (13)
and the total time effect entropy is summed as
![]() . (14)
. (14)
The biggest time effect entropy is
![]() . (15)
. (15)
The time effect order degree of system is defined to be
![]() . (16)
. (16)
3.2. Improved Quality Entropy Model
Quality entropy of subsystem vi is defined as
![]() , (17)
, (17)
d−(vi) is called the quality microscopic state of vi, which is equal to the number of its direct upstream systems. Let ![]() denote the total quality microscopic state.
denote the total quality microscopic state.
Quality entropy of vi is
![]() , (18)
, (18)
the total quality entropy is summed as
![]() , (19)
, (19)
and the biggest quality entropy is
![]() . (20)
. (20)
Thus, quality order degree of the system is expressed as
![]() , (21)
, (21)
and order degree of the system is synthesized as
![]() . (22)
. (22)
Within a certain range, the bigger the order degree is, the system is more likely to provide high quality information.
4. Case Study
4.1. Problems Description
To illustrate the proposed model and compare order degree under the two scenarios, the paper implements our model in an elevator manufacturing enterprise. The enterprise comes to realize that direction of information flow between subsystems can heavily impact on timeliness and accuracy of information. Moreover, to quickly response to dynamic environment, the enterprise has to combing information flow between subsystems in order to improve chaotic state in transferring information. Figure 2(b) shows the current structure of information system in the enterprise. To facilitate our research, research object is the system at the application level which does not contain operating system, safety management system and other systems. As shown in Figure 2(b), there are eleven subsystems and each subsystem does not integrate other subsystems.
According the evaluation method of order degree in literature [6] , the information flow between two subsystems is non-directional, and the corresponding structure is displayed as Figure 2(a). In fact, information flow has definite directions which affects the timeless and accuracy of information by altering the shortest path between any two systems and in-degree of each system.
4.2. Results Analysis
1) From Table 1, we obtain that time effect order degree of information system increases under the directed information flow, which indicates the information system with definite direction of transferring information is more effectively to guarantee the timeliness of information. Theoretically, homogeneous information flow shortens the shortest path between subsystems and then improves timeliness of information. However, too much direct upstream systems make each subsystem analyzes and verifies per unit information blindly and randomly, which consumes a lot of time. Directed information flow makes information transition more definite and fluent so that information can be transmitted in order. Thus, the value of time effect order degree increases from 0.1224 to 0.1360.
2) Similarly, from Table 2, we find that directed information flow reduces quality order degree, which means the information system with definite direction of transferring information is less effectively to guarantee the accuracy of information. Homogeneous information flow makes each subsystem have more direct upstream systems so that system analyzes and verifies per unit information that passing from its directed upstream system repeatedly. Consequently, quality degree of information system decreases from 0.4050 to 0.4040.
3) In the case, order degree of information system is equal to 0.5274 when directed information flow is neglected, and the value of order degree is 0.5400 when directed information flow is incorporated. Directed information flow leads to a bigger order degree, which indicates that definite direction of transmitting information exerts positive effects on information system. Information system, as dissipative system, should maintain its order degree within the range [Omin, Omax]. Only in this interval can system operate smoothly. Information systems with too big and too small order degree are unstable. The actual value of order degree in the case is 0.5400. Information system operates orderly at this moment, which means 0.5400 is within the interval [Omin, Omax]. The value of order degree is 0.5274 when the enterprise evaluates order degree of information system without considering directed information flow. If 0.5274 is within the interval [0, Omin], enterprise will input plentiful resources to find out factors that affect the stability of information system. However, system is in a normal operating state at this moment. Thus, unnecessary waste occurs. If 0.5274 is within the range [Omin, Omax], a waste of resources can be avoided but unexpected result is that enterprise will be in a discouraged state because the enterprise mistakes that its information system has low order degree.
![]() (a)
(a)![]() (b)
(b)
Figure 2. (a) System structure neglects directed information flow; (b) System structure incorporates directed information flow.
In conclusion, directed information flow in real-world information system reduces accuracy of information but it increases timeliness of information, which can be illustrated in practice. For example, reducing unnecessary roads in transportation system eases traffic jam and reduces time to the destination; explicit direction of
![]()
Table 1. A comparison between both time effect entropy appraisal.
![]()
Table 2. A comparison between both quality entropy appraisal.
information flow in enterprise organization structure speeds up delivery of information, but it reduces information sources of each decision-making agent, which ultimately make decision makers acquire lower accurate information. Improved structural entropy suits better to actual structure of information system and research results will facilitate management activities.
5. Conclusions
From the perspective of the interactions between the subsystems, an improved structural entropy is proposed to evaluate the order degree of information system. The paper compares the differences of timeliness, quality order degree and synthetic order degree of information systems between the system with non-directional information flow and the system with directed information flow. Result indicates that direction of information transmission between subsystems has a positive effect on the operation of enterprise information system. Our analysis yields a number of managerial insights. First, given that directed information flow effectively improves the timeliness, the enterprise needs to ensure that its information system and organizational structure have definite directions to transfer information. Only in this way can enterprise sensitively percept the environmental change and quickly response to it. Second, specifying the direction of transferring information may reduce the accuracy of information, but it decreases cost through reducing blind, random and repeated analysis and verification of information from the direct upstream systems. If the reduced cost exceeds the loss caused by the decreased accuracy of information, specifying direction of information system will have a positive effect on information system. Last but not least, a company cannot owe the timeliness and accuracy at the same time, but the accuracy of information is the premise to the development of enterprises. On condition that accuracy of information can satisfy requirements, enterprise can take action to enhance its sensitivity to response to the external requirements and to achieve the foregoing advantages, which is significant to a responsive organization. In addition, within a certain range, increasing the order degree will improve the operation efficiency of systems. The order degree beyond the range indicates the instability of systems. Thus, enterprise should keep the order degree within a reasonable range to maintain the stable operation of systems.
Considering the actual situation, this paper proposes an improved algorithm of the structure entropy model to evaluate the order degree of information system from a micro level, which increases the reliability of order degree. The improved structural entropy model is suitable not only for the information system, but also for other sys- tems such as organizational system and transport system. However, assessment of order degree should be multi- angles, which is one of the following research focuses. Moreover, self-organization evolvement of information system, resource configuration process and robustness analysis of information system are also research focuses in the future.
Acknowledgements
Authors would like to acknowledge the financial support from National Natural Science Foundation of China (No. 50675069).