1. Introduction
This paper is dedicated to military pilots who have the audacity to take off in experimental aircraft, and, with even greater audacity, have high expectations of landing such complicated machinery in one piece. Perhaps their descendents will fly craft mathematically described in this paper, or, more ominously, perhaps some military pilots, both past and present, have already encountered such craft in their nearby airspace!
This paper attempts to delve into the mystery of space travel. Consequently, it will be necessary to re-examine concepts which scientists hold dear. In addition, it is the author’s contention that the so-called weak force is the seat of a powerful new energy source which can be used to propel spacecraft to be unheard of velocities utilizing a variable scalar gravitational “constant” (see Section 9).
The approach will be to use a complex mass-velocity vector (not momentum vector) over the usual four dimensional space-time manifold domain. This complex mass-velocity vector is considered to be a function of the underlying four dimensional coordinates of this manifold domain.
The Lorentz space-time metric 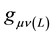 is the one used in deep space with a signature in a Lorentzian space- time of (−1 −1 −1 + 1) and will be used to raise and lower indices and is not considered changed or modified by any of the above considerations; however,
is the one used in deep space with a signature in a Lorentzian space- time of (−1 −1 −1 + 1) and will be used to raise and lower indices and is not considered changed or modified by any of the above considerations; however, 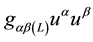 will be essentially interpreted from a new point of view by introducing a generalization. One of the major obstacles faced is that normally the so-called “arc length” ds will be equal to zero at the speed of light (because of its dependence upon relative velocity), and since ds is used in the denominator of equations of motion, such equations will become meaningless. This paper will continue to use the arc length ds, along with its implied proper time; however, this paper will use a different method of approach to this problem which will involve divorcing ds from its dependence upon relative velocity as a result of the aforementioned generalization.
will be essentially interpreted from a new point of view by introducing a generalization. One of the major obstacles faced is that normally the so-called “arc length” ds will be equal to zero at the speed of light (because of its dependence upon relative velocity), and since ds is used in the denominator of equations of motion, such equations will become meaningless. This paper will continue to use the arc length ds, along with its implied proper time; however, this paper will use a different method of approach to this problem which will involve divorcing ds from its dependence upon relative velocity as a result of the aforementioned generalization.
The advent of the problem of galaxy rotation due to the presence of so-called “dark matter” seems to imply that a majority of the solar systems in a galaxy move through their respective galaxy at roughly the same velocity implying that there is a background differential time coordinate dt which can be considered to be approximately the same most everywhere where these solar systems are in that part of the galaxy rotation curve which denotes a constant speed.
2. Mass-Velocity Vector [1]
The mass-velocity vector will be defined as follows:
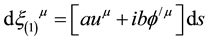 (1)
(1)
where 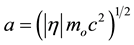 and
and 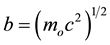 and
and 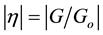 where
where 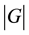 is the absolute magnitude of a variable scalar gravitational “constant” and is assumed to be generally complex, and, hence; dependent upon space and time coordinates (and therefore capable of being Fourier analyzed or at least to a degree, stochastic, such as the time dependence of raindrops on a roof).
is the absolute magnitude of a variable scalar gravitational “constant” and is assumed to be generally complex, and, hence; dependent upon space and time coordinates (and therefore capable of being Fourier analyzed or at least to a degree, stochastic, such as the time dependence of raindrops on a roof). 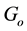 is the usual gravitational “constant”;
is the usual gravitational “constant”; 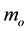 is the mass of the spacecraft in its rest frame, and
is the mass of the spacecraft in its rest frame, and  is the four velocity
is the four velocity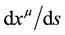 .
.
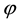 must have the dimensions of cm since
must have the dimensions of cm since 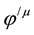 is dimensionless.
is dimensionless. 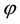 is produced by the new “electric” dipole p (esu×cm) of the weak force. The simplest way to define
is produced by the new “electric” dipole p (esu×cm) of the weak force. The simplest way to define 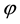 is to just let
is to just let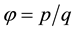 , where
, where ![]() and where p has the dimensions of esu cm (see Section 9).
and where p has the dimensions of esu cm (see Section 9).
The mass-velocity vector is introduced, because it is assumed that a gradient in ![]() or i.e.
or i.e. ![]() (to be controlled from within the spacecraft) will cause not only a change in the velocity of the spacecraft but, in addition, will also cause a change in the apparent inertial/gravitational mass mo of the spacecraft in a coordinated way. This is the guiding principle of this paper! This is not so outlandish as one would assume, simply because of the following example.
(to be controlled from within the spacecraft) will cause not only a change in the velocity of the spacecraft but, in addition, will also cause a change in the apparent inertial/gravitational mass mo of the spacecraft in a coordinated way. This is the guiding principle of this paper! This is not so outlandish as one would assume, simply because of the following example.
Suppose an asteroid, located quite a distance from the earth yet still within the gravitational attraction of the earth, entered a small region of space which was governed by a different gravitational constant G. The gravitational force on the asteroid would then be
![]()
where R is the distance from the center of the earth. This can be recast into the standard form such as follows
![]() .
.
where![]() .
.
Thus we see that the apparent inertial/gravitational mass of the asteroid has changed due to the factor![]() . This is why
. This is why ![]() appears in a.
appears in a.
The author is further assuming that the creation of this macroscopic field φ is somewhat similar to the creation of a laser beam, that is, that a large number of tiny effects from the many nucleons of the many atoms/molecules of the spacecraft that they are associated with, when add together, will form a large macroscopic effect surrounding the spacecraft.
We now need to determine the dependence of ![]() upon
upon![]() . From Section 9, we have
. From Section 9, we have ![]() from which we can calculate that
from which we can calculate that ![]() and hence
and hence![]() .
. ![]() At once we can see that as
At once we can see that as ![]() (or
(or![]() ) that
) that![]() . Also, as
. Also, as![]() , then
, then ![]() and
and![]() .
.
The gradient of ![]() is given by
is given by
![]()
The method of attack on this problem will be as follows. ![]() will be treated as a “vector” in complex space, in the sense that we will be taking a product in the +i direction, then a product in the −i direction then adding these two products together and taking an average. We therefore introduce a second mass-velocity vector
will be treated as a “vector” in complex space, in the sense that we will be taking a product in the +i direction, then a product in the −i direction then adding these two products together and taking an average. We therefore introduce a second mass-velocity vector
![]() (2)
(2)
where ![]() is the complex conjugate of
is the complex conjugate of ![]() but with a different vector index from (1).
but with a different vector index from (1).
Consequently, we must also allow the following mass-velocity vectors
![]() (3)
(3)
and
![]() (4)
(4)
We now form the following asymmetric tensor
![]() (4a)
(4a)
![]()
![]()
Let ![]() = Equation 4(a).
= Equation 4(a).
![]() (5)
(5)
where ![]() can be interpreted as a rarely defined Lagrangian tensor and
can be interpreted as a rarely defined Lagrangian tensor and
![]() with the dimensions of energy (5a)
with the dimensions of energy (5a)
Tμν can be defined as the kinetic energy part of this Lagrangian tensor
![]() (5b)
(5b)
![]() can be defined as the potential energy part of this Lagrangian tensor.
can be defined as the potential energy part of this Lagrangian tensor.
![]() is Hermitian (observable), symmetric and with dimensions of energy.
is Hermitian (observable), symmetric and with dimensions of energy.
![]() (5c)
(5c)
![]() is Hermitian (observable), antisymmetric and with dimensions of energy.
is Hermitian (observable), antisymmetric and with dimensions of energy.
We note that ![]() which is the definition of Hermitian or
which is the definition of Hermitian or![]() .
.
We will now try to find a simple meaning for ![]() noting that it is anti-symmetric. Noting that
noting that it is anti-symmetric. Noting that
![]()
we obtain
![]() (5d)
(5d)
The dimensions of ![]() are ergs.
are ergs.
![]()
We shall deal with these tensorial matters later.
3. A Structural Lagrangian
Thus we see that the asymmetric complex tensor, which we call the Lagrangian tensor in (5) naturally breaks up into two parts, a symmetric part to the left of i and an antisymmetric part to the right of i.
The contraction of (5) with the metric tensor ![]() yields the inner product
yields the inner product
![]() (6)
(6)
where
![]() due to its antisymmetry
due to its antisymmetry
![]()
![]()
We note that ![]() is similar in mathematical structure to a Lagrangian, with T the kinetic energy and V the potential energy.
is similar in mathematical structure to a Lagrangian, with T the kinetic energy and V the potential energy.
It therefore seems appropriate to utilize the Euler-Lagrange equations:
![]()
![]()
![]() (6a)
(6a)
![]() (6b)
(6b)
Upon Equations 6(a) and 6(b), we obtain and upon multiplying both sides by ![]()
![]() (7)
(7)
4. A Constant of the Motion
Contracting (7) with ![]()
![]()
![]()
![]() (8)
(8)
![]() (8a)
(8a)
where ![]()
5. Necessary Conditions for the Viability of Space Travel
This Equation 8(a) is what will be interpreted as the generalization of ![]() in the sense that (ds)2 is no longer required, in this general case, to be equal to
in the sense that (ds)2 is no longer required, in this general case, to be equal to![]() .
.
![]()
![]()
![]()
![]()
Letting ![]() where dτ is the time aboard the spacecraft and dt is technically the time differential at the spacecraft’s home planet, but can be considered as the background differential time coordinate discussed in the paragraph on galaxy rotation. Solving for
where dτ is the time aboard the spacecraft and dt is technically the time differential at the spacecraft’s home planet, but can be considered as the background differential time coordinate discussed in the paragraph on galaxy rotation. Solving for ![]() we obtain
we obtain
![]()
Space travel will not be practical or viable unless the crew of a spacecraft can be assured of returning to the same civilization that they left. This then imposes the two very important conditions, viz., 1) ![]() and 2) velocities greater than the speed of light. We thus have the following conditions:
and 2) velocities greater than the speed of light. We thus have the following conditions:
![]()
and
![]()
![]()
![]()
![]()
![]()
Let us look again at Equation 8(a)
![]()
![]()
Therefore, when the spacecraft turns off its field, the usual space-time conditions, which we are familiar with on ds, once again apply.
6. Acceleration Equation
Let us look again at Equation (7):
![]()
From ![]() we have
we have ![]()
Thus we can see that moc2 cancels out of this acceleration equation giving
![]() (9)
(9)
Conclusion: An acceleration equation without mass implies inertialess acceleration.
7. A New Type of ‘Electromagnetic’ Field with a Magnetic Monopole Feature
If we divide both sides of Equation (5d) by qRoc then define a new tensor by ![]() which has the dimensions of (esu/cm2) or that of an electromagnetic field, bearing in mind the antisymmetry of
which has the dimensions of (esu/cm2) or that of an electromagnetic field, bearing in mind the antisymmetry of![]() .
.
![]() (10)
(10)
![]()
Thus we come to the conclusion that Equation (10) may represent a new type of “electromagnetic field phenomena” associated with this new perspective on advanced space travel. In the equation
![]()
![]() is related to a new type of “electromagnetic” field process, while
is related to a new type of “electromagnetic” field process, while ![]() is related to a symmetric tensor type process, since a type of “pressure gradient” seems to be derivable from
is related to a symmetric tensor type process, since a type of “pressure gradient” seems to be derivable from![]() , as noted from the acceleration Equation (9), this seems to provide the justification for viewing
, as noted from the acceleration Equation (9), this seems to provide the justification for viewing ![]() as some type of space-time stress tensor.
as some type of space-time stress tensor. ![]() represents a kinetic energy tensor of motion of the spacecraft.
represents a kinetic energy tensor of motion of the spacecraft.
![]()
Since ![]() is proportional to
is proportional to![]() , it is easier to conceptualize some ideas by performing the following calculations using the φ’s instead of the η’s.
, it is easier to conceptualize some ideas by performing the following calculations using the φ’s instead of the η’s.
![]()
![]() and similarly for its complex conjugate.
and similarly for its complex conjugate.
Now let us calculate the antisymmetrized sum of ![]() denoted by
denoted by![]() .
.
![]() (11)
(11)
![]()
where ![]() indicates the variables that this sum is to be over, but since
indicates the variables that this sum is to be over, but since ![]() this reduces to
this reduces to
![]()
![]()
![]() (11a)
(11a)
![]() is just the complex conjugate of Equation (11).
is just the complex conjugate of Equation (11).
![]() (11b)
(11b)
![]() (11c)
(11c)
We also have
![]()
![]() (11d)
(11d)
We know from Maxwellian electromagnetic theory that the usual Maxwell electromagnetic tensor ![]() can be represented as
can be represented as
![]()
where Aμ is the Maxwell four potential.
Further, ![]() means that the antisymmetrized sum is zero which means that there are no magnetic monopoles in Maxwellian electromagnetic theory, as is well known. In startling contrast, however, we immediately notice that
means that the antisymmetrized sum is zero which means that there are no magnetic monopoles in Maxwellian electromagnetic theory, as is well known. In startling contrast, however, we immediately notice that ![]() implying that there is a magnetic monopole type feature associated with this new electromagnetic field.
implying that there is a magnetic monopole type feature associated with this new electromagnetic field.
8. The Magnetic Monopole’s Rotational Feature
Another startling observation is that in the calculation of Equation 11(d), the tensor ![]() appears. The presence of the tensor
appears. The presence of the tensor ![]() means that the velocity field
means that the velocity field ![]() is not entirely translational and that this tensor selects out those places in the velocity field
is not entirely translational and that this tensor selects out those places in the velocity field ![]() which have a vortex motion, i.e. a circulation or rotation. It is not proper to split
which have a vortex motion, i.e. a circulation or rotation. It is not proper to split ![]() into a translational part and a rotational part since
into a translational part and a rotational part since ![]() is a true vector and rotational velocity is an axial or pseudo vector as its direction changes with the handedness of the coordinate system. The tensor
is a true vector and rotational velocity is an axial or pseudo vector as its direction changes with the handedness of the coordinate system. The tensor ![]() is the only proper way to handle rotation in a true tensorial way. Thus, when the tensor
is the only proper way to handle rotation in a true tensorial way. Thus, when the tensor ![]() is evaluated for ν, α = 1, 2, 3, we obtain the components of the well known three dimensional rot or curl or ´∇ operator in vector analysis. Further, we know from the theory of ordinary fluid flow that such a three dimensional rotation can be expressed by the following equation
is evaluated for ν, α = 1, 2, 3, we obtain the components of the well known three dimensional rot or curl or ´∇ operator in vector analysis. Further, we know from the theory of ordinary fluid flow that such a three dimensional rotation can be expressed by the following equation
![]()
Therefore, the tensor ![]() indicates that this magnetic monopole feature has a rotational aspect associated with it.
indicates that this magnetic monopole feature has a rotational aspect associated with it.
9. Is the Weak Interaction Harboring a Powerful Energy Source? [2]
Just what is the plausible physical nature of the weak interaction? This endeavor starts out by noticing the similarity in values of two particular numbers. We begin by giving the following sets of values which will be used in the calculation of those two numbers.
Mw = considered to be the average boson mass of the weak force = 91mp;
mp = mass of the proton = 1.673 ´ 10−24 g;
me = mass of the electron = 9.109 ´ 10−28 g;
h = Planck’s constant = 6.626 ´ 10−27 erg・sec;
Go = gravitational constant = 6.670 ´ 10−8 dyne・cm2・g−2.
![]()
RoA = a value, which is assumed to be comparable to the range of the weak force = ~10−17 cm;
c = speed of light = 3 ´ 1010 cm・sec−1.
![]()
The first number N1 to be calculated is
![]()
where ![]()
![]()
![]()
The second number N2 to be calculated is
![]()
![]()
It is extremely coincidental that these two numbers are that close. The hypothesis of this paper is that these are, in reality, an equivalence, viz., N1 = N2 or
![]()
When this assumption is made, a calculated value RoC from this postulated equivalence is
![]()
or
![]() ,
,
which is roughly ten times less than the value calculated from the uncertainty principle for the vector boson of 91mp.
Could this particular set of dimensions, cm・g3, be especially predisposed to a relationship between the weak interaction and the gravitational “constant”? We can explore this possibility further by attempting to create a simple non-quantum mechanical model of the weak interaction in order to determine its true nature.
To this end, let the model begin with a tiny variable electric dipole according to the following equation
![]() ,
,
where![]() ,
, ![]() ,
, ![]() , where
, where![]() , G now considered to be a real scalar variable for computational purposes.
, G now considered to be a real scalar variable for computational purposes.
We then form the square of p, ![]() , noting that esu2×cm2 = erg×cm3.
, noting that esu2×cm2 = erg×cm3.
We now posit that the weak interaction is activated by the variable![]() . Then we can take the limit
. Then we can take the limit
![]()
![]()
![]() .
.
We already know that the Fermi weak interaction constant is ![]() so that this simplistic model is somewhat instructive [3] . It is to be emphasized that this is a model and not a theory. If a successful theory incorporating a variable gravitational ‘constant’ into the weak interaction is ever developed, then one of the expectations is that this model, or something close to it, would possibly be derived.
so that this simplistic model is somewhat instructive [3] . It is to be emphasized that this is a model and not a theory. If a successful theory incorporating a variable gravitational ‘constant’ into the weak interaction is ever developed, then one of the expectations is that this model, or something close to it, would possibly be derived.
What the above hopefully shows is the possibility of a relationship between the gravitational ‘constant’ and the weak interaction. Assuming that this is the case, how could this posited assertion be verified experimentally?
One way is by calculating (using the uncertainty principle) the mass associated with the value![]() . This value is
. This value is![]() . If this theory is correct, then CERN should find a new particle at around 1118 times the mass of the proton.
. If this theory is correct, then CERN should find a new particle at around 1118 times the mass of the proton.
We know that energy levels, whether nuclear or orbital, are properties of the atom as a whole. We also know that the wave amplitudes for some orbital electrons fall within the nucleus. Thus it should come as no surprise that if a nucleus needs to change to a lower energy level, it has the option of ejecting an orbital electron, called an Auger electron (internal conversion process). This is a powerful concept! The nuclear energy levels can effect a change in the orbital energy levels. The question, which is now obvious, is whether or not this process is reversible. Can an orbital electron energy level effect a change in a nuclear energy level? In the case of this paper, can a change in the orbital energy levels effect a change in the weak interaction energy levels, through a manipulation of the entire atomic wave amplitude, thus manifesting a macroscopic variability in the gravitational “constant”? It is known that the process of beta decay emits electrons in a seeming continuous spectrum of energy levels ranging from a few kilovolts to the relativistic range of 15 Mev or more. A continuum of energy levels is a concept straight out of the pre-quantum mechanics period known as the classical period. This would seem to indicate a scalar activity of some sort and not a quantum activity.
Altering electronic energy levels could characterize the procedure involved in the combustion process. What is combustion? It is one or more molecular reactants (a fuel, an oxidant, and/or heat and/or a catalyst) producing one or more products of combustion plus heat through an intervening procedure consisting of a scrambling of orbital electron energy levels (via the probability amplitudes of the reactants and the products) until an equilibrium in such levels is attained for all the products involved. The question is whether or not there exists a singular set of combustion reactants, which, when ignited, will induce an excitational resonance, via the orbital probability amplitudes overlapping the nucleus in the weak interaction, and cause it to unleash a macroscopic variable gravitational ‘constant’?
The many-body problem has never been solved, but most assuredly involves extremely complicated non-linear solutions; however, such solutions, in the absence of combustion, must exist, otherwise clouds of electrons could not remain in a stable situation around atoms with atomic numbers Z > 2. To put another way, when applied to the atom, is it possible, in the absence of combustion, that there could exist many-body solutions of wave amplitudes of the atom which allow for a more or less direct exchange of information between orbital electrons and the neutrons in the nucleus? Usually, as in the case of the Auger electron, the information is sent one-way from the nucleus to the electron. Can this flow of information be reversed and tremendously amplified in the presence of combustion of the presumed singular set of combustion reactants so that information is sent from the orbital electrons to the nuclear weak interaction?
As mentioned earlier, a macroscopic field in this paper is seen to be the final effect, like a laser beam, of many many tiny effects added together.
If this reversibility can truly occur, then a powerful new energy source could be tapped, based upon a macroscopic variable gravitational “constant”, which would have tremendous upside potential in transportation, space exploration, and military applications. The only way to know for sure is to find that singular experimentum crucis!
The charged W boson particle has a rest energy of 80.385 Mev and when divided by the energy of the proton 938.272 yeilds 85.673mp. Likewise the neutral Z boson has a rest energy of 91.187 Mev and when divided by the energy of the proton 938.272 yields 97.186mp. Then the arithmetic average is![]() . However, the author questions whether the straight arithmetic average is the proper way to find the average between a charged particle and a neutral particle, simply, because of the possibility of there being three independent sources for the intertia of objects.
. However, the author questions whether the straight arithmetic average is the proper way to find the average between a charged particle and a neutral particle, simply, because of the possibility of there being three independent sources for the intertia of objects.
1) The Higgs particle/field is the source of inertia for all other particles: this is according to current particle theorist views.
2) Consider why a photon does not travel at infinite speed. Also consider why an Olympic runner on flat hard ground can run faster than a man slogging his way through a swamp wearing heavy boots in eight inches of mud. Something is slowing the photon down giving it the appearance of having inertia. That something from Maxwell theory is the product of the free space permeability and permitivity constants. The ability of space-time to store electromagnetic energy gives an inertia to the photon, which resists an acceleration to a higher velocity.
3) This paper also contributes to an apparent inertial/gravitational mass given by![]() , which is another source of inertia or the lack thereof.
, which is another source of inertia or the lack thereof.
With three different sources of inertia, is it really valid to take a straight arithmetic average (especially between charged and uncharged particles) or is some type of weighted average really the proper course to take. The author believes that the proper weighted average, when found, will yield 91mp and not the 91.43mp.
10. Conclusions
The author believes that this theory may provide a practical method for interstellar space travel if and when the generator for the fields talked about in this paper can be somehow pried from the nucleons associated with the weak interaction. These fields provide the means for inertia-less acceleration and for what looks like a new type of electromagnetic field, with its associated magnetic monopole. One obvious danger of a macroscopic magnetic monopole field is due to the fact that currents come to a halt near a magnetic monopole, per Ampere’s law. Vehicles with electric ignition systems will be most affected; however, diesel engines probably will not be affected, since they depend solely upon compression of diesel fuel for ignition. Biological life forms also have currents running through their nerve fibers, and, as a result, there will be a very high danger of paralysis or even death near such a macroscopic field due to the cessation of these biologically generated currents.
As everyone knows, Faraday cages defeat Maxwellian electromagnetic fields. Examples of common Faraday cages or good approximations thereto are airplanes, school buses, cars and hoods on cars. The new type of electromagnetic field derived in this paper has greater penetrating power than Maxwellian fields and will be able to defeat the purpose of a Faraday cage and affect the flow of currents inside which is protected by the cage. This is due to this new type of electromagnetic field depending on the gradient in the supposed gravitational “constant”, such gradient being unaffected by the presence of the Faraday cage, occurring both externally and internally to the cage.
Rotation is also associated with this magnetic monopole. It is unclear whether the rotation is generated automatically or whether the rotation is an independent variable which can be utilized by the crew of the spacecraft to further manipulate the fields.
Since the time interval in the frame of reference of this spacecraft and the coordinate time interval in the reference frame of the source planet remain the same, there is an implied certainty that significant space travel over interstellar distances may occur during the lifetime of an explorer for sufficiently high velocities in excess of the speed of light, with the added bonus being that the explorer will be able to return to the same civilization that he/she leaves on the source planet. Such extremely high velocities in excess of the speed of light may give pause for concern in deep space where interaction with particles of rock and dust will occur. It is to be noted that due to the equation![]() , since
, since ![]() and as this supposed complex scalar approaches zero, this spacecraft is surrounded by a very sharp and powerful gradient in
and as this supposed complex scalar approaches zero, this spacecraft is surrounded by a very sharp and powerful gradient in ![]() due to the factor of
due to the factor of![]() . This powerful gradient will act as a deflector that protects the spacecraft against rock and dust at ultra high speeds.
. This powerful gradient will act as a deflector that protects the spacecraft against rock and dust at ultra high speeds.
The presumption is that the spacecraft will be operating in the environment of outer space which provides an airless vacuum. However, there does not seem to be any reason why such a craft will not be able to operate within a gaseous or liquid medium, as well, taking note of the possibility that particles of the gaseous or liquid medium near the crafts accelerating field will themselves be accelerated along with the craft. This may mean that each time such a craft leaves the atmosphere of a planet, the accelerating field tears away a small amount of the atmosphere which is never to be replaced. Also, due to the factor of![]() , the apparent mass of the spacecraft will be close to zero, indicating that there will probably be no sonic booms occuring at extreme velocities in a planet’s atmosphere.
, the apparent mass of the spacecraft will be close to zero, indicating that there will probably be no sonic booms occuring at extreme velocities in a planet’s atmosphere.