Throughput Estimation with Noise Uncertainty for Cyclostationary Feature Detector in Cognitive Radio Network ()
1. Introduction
Cognitive radio networks are one of the enabling technologies for future communication and networking [1] . Cognitive radio depends on Dynamic Spectrum Access (DSA) which allows secondary users (SUs) to occupy the unused spectrum instead of keeping it idle or unused by the primary user (PU) [2] . The first function of the cognitive radio networks which is called the spectrum sensing senses the free spectrum bands and the presence or absence of the primary user [3] [4] . After sensing the spectrum management will take place by selecting the best band, spectrum sharing and allocation by coordinating fair spectrum access to this channel with other users, and finally spectrum mobility by vacating the channel when a licensed user is detected.
Spectrum sensing can be divided into two main categories cooperative detection technique and noncooperative. In the cooperative detection secondary users collect the information regarding channel occupancy and transmit this information into spectrum map that updated periodically. In non-cooperative detection, individual radios act locally and autonomously to carry out their own spectrum occupancy measurements and analysis. It can be divided into two classes blind sensing which does not need any information about the primary user signal such as energy detector, and signal specific sensing which need information about the primary user signal such as matched filter and feature detector [3] .
According to IEEE 802.22 wireless regional area networks (WRAN), each medium access control (MAC) frame consists of one sensing slot and one data transmission slot, and thus periodic spectrum sensing should be carried out such that the cognitive radio users can decide whether the next frame can continue to transmit on the spectrum band [5] [6] . Associated with spectrum sensing are two parameters: probability of detection and probability of false alarm. The higher the detection probability, the better the primary users can be protected. However, from the secondary users’ perspective, the lower the false alarm probability, the more chances the channel can be reused when it is available, thus the higher the achievable throughput for the secondary users. Thus there could exist a fundamental tradeoff between sensing capability and achievable throughput for CR different detectors [7] .
This paper is organized as follows: Section 2 investigates the related work in throughput in cyclostationary feature detectors in CRN; Section 3 discusses the system model and its assumptions; Section 4 presents the numerical results; and Section 5 gives the conclusion and the future work.
2. Related Work
CRN has to enforce quiet periods to effectively sense the spectrum availability to protect the PUs. Spectrum sensing and sensing time length can vary depending on the algorithm according to [8] . In cooperative sensing, the length of sensing time at individual SUs is proportional to the sensing accuracy increasing sensing time decreases the transmission time. The trade-off is called the sensing efficiency problem and is discussed in [9] and [10] . In [11] the CRN system throughput is maximized by cooperative sensing. Optimal spectrum sensing time considering spectrum handoff due to false alarm discussed in [12] . As in [13] , sensing decision problem for maximizing the system throughput is discussed. Also in [13] a suggested algorithm to maximizing the throughput by cooperative sensing is suggested. In [14] , maximizing secondary network throughput while keeping under control the average interference is formulated. Authors in [15] study the effect of noise uncertainty on choosing the minimum number of samples in energy and matched filter detectors. The authors in [16] propose a fast spectrum detecting algorithm based on cyclic autocorrelation of communication signals and select the users with good detection performance to cooperative sense to improve sensing sensitivity without considering noise uncertainty. In [17] a comparison of sensing algorithms which revealed wide variability in their computational complexity for the targeted detection performance without considering network throughput is presented. Authors in [18] propose novel spectrum sensing algorithm, and examines the sensing throughput tradeoff for energy detector in CRN under noise variance uncertainty.
3. System Model
The problem of signal detection in additive Gaussian noise can be formulated as a binary hypothesis testing problem with the following hypotheses:
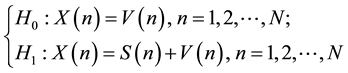 (1)
(1)
where X(n), S(n) and V(n) are the received signals at CR nodes, transmitted signals at primary nodes and white noise samples, respectively; H1 and H0 stand for the decision that the licensed user is present or not, respectively. Noise samples V(n) are from additive white Gaussian noise process with power spectral density σ2 [19] .
Feature detector in CR network operates in the mid-way between Energy and Matched filter detectors. The cyclostationary feature detector relies on the fact that most signals exhibit periodic features, present in pilots, cyclic prefixes, modulations, carriers, and other repetitive characteristics. Because the noise is not periodic, the signal can be successfully detected [16] -[18] .
The feature detector correlates received signal X(n) with frequency shifted version of itself resulting in spectral correlation function (SCF) [19] .
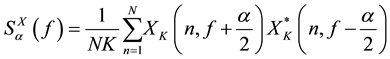 (2)
(2)
Here XK(n, f) is the K point FFT around sample n and α is the amount of frequency shift. The decision statistic is modeled in this SCF and it is compared against given threshold γ.
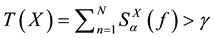 (3)
(3)
The probability of false alarm and the probability of detection can be given as [19]
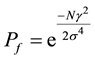 (4)
(4)
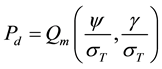 (5)
(5)
where, 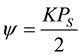 ,
, 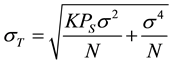 , FT points [19] . And Qm(.) is the first order Marcum Q functionac-
, FT points [19] . And Qm(.) is the first order Marcum Q functionac-
cording to [20] and given in Equation (6).
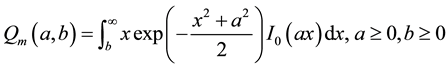 (6)
(6)
where I0(.) is the zeroth-order modified Bessel function given in Equation (7)
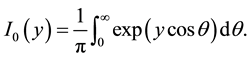 (7)
(7)
Solving for γ to get detection probability
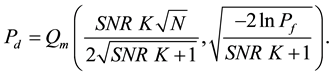 (8)
(8)
Denote C0 as the throughput of the secondary network in the absence of PU, C1 is the throughput in the presence of PU, so the throughput C of the secondary network according to [21] will given by
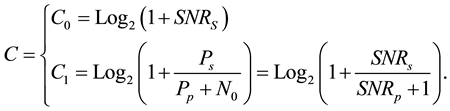 (9)
(9)
The normalized rate for unit bandwidth for the secondary network with sensing slot time τ and a frame duration time T under hypothesis H0 and H1 are given by
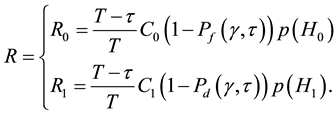 (10)
(10)
And the average throughput for the secondary network will given by
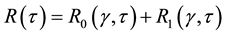
 (11)
(11)
For cyclostationary feature detector Pf and Pd are given from Equations (4) and (5) then the average throughput for the secondary network will be
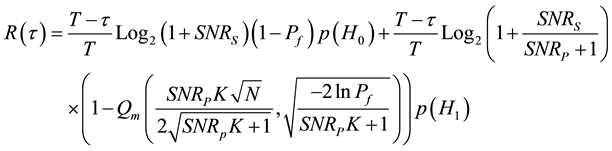 (12)
(12)
Due to noise uncertainty, the estimated noise power may be different from the actual noise power. Let the estimated noise power changed in the interval 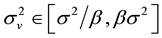 where β > 1 is the noise uncertainty factor. For feature detector and in a noise variation environment, minimizing the Marcum Q function in Pd and maximizing Pf, with threshold γ, hence
where β > 1 is the noise uncertainty factor. For feature detector and in a noise variation environment, minimizing the Marcum Q function in Pd and maximizing Pf, with threshold γ, hence
![]() (13)
(13)
The threshold will given by
![]() (14)
(14)
According to [22] and Equation (5) when ![]() decreased and
decreased and ![]() increased the value of Marcum Q function decreased
increased the value of Marcum Q function decreased
![]() (15)
(15)
Modifying (12) to show the effect of noise variation on throughput in cyclostationary feature detector will give
![]() (16)
(16)
where ![]() and Pf is given by Equation (13).
and Pf is given by Equation (13).
4. Numerical Results
In this section, numerical results are presented to evaluate the sensing-throughput trade-off with noise uncertainty for feature detector scheme. Table 1 summarizes the numerical values used in the paper according to [7] and [8] .
Probability of detection versus probability of false alarm with SNR variation for feature detector is shown in Figure 1. As it could expected, the performance of feature detector decreases with SNR. The receiver operating characteristic curve (ROC) with noise uncertainty is shown in Figure 2. Curves displayed in Figure 2 are calculated numerically. Value of SNR is −20 dB with 1 ms sensing time and corresponding values of Pd are calculated with Equation (13). The noise uncertainty factor of receiving device is normally up to 1.585 [23] .
![]()
Figure 1. Effect of SNR on the feature detector receiver operating characteristics.
![]()
Figure 2. Receiver operating characteristics of feature detector with noise uncertainty.
The effect of different noise uncertainty factor values on probability of detection with variable SNR values with 0.01 false alarm probability is shown in Figure 3. The figure shows that SNR value between −18 to −20 dB has dramatically effect on detection probability.
Figure 4 shows the effect of sensing time on normalized secondary network throughput with −20 dB SNR value, and 1.5 noise uncertainty factor. Figure 5 shows that 20 ms sensing time or spending 2% of total time to sense the spectrum will get 99% probability of detection regardless of 50% noise uncertainty change.
Figure 6 shows the effect of noise uncertainty on the secondary network throughput with −20 dB SNR, and 0.01 probability of false alarm. The figure shows that increasing the uncertainty factor from 1.05 to 1.5 leads to changing the overall throughput by 8%.
5. Conclusion and Future Work
The effect of noise uncertainty on the secondary network throughput with low SNR values is analyzed. Moreover,
![]()
Figure 3. SNR versus Pd with variable noise uncertainty factor.
![]()
Figure 4. Effect of sensing time on normalized secondary network through- put.
![]()
Figure 5. Probability of detection (Pd) versus sensing time for with noise uncertainty.
![]()
Figure 6. Normalized secondary network throughput versus sensing time with noise uncertainty.
selecting the sensing time with the proper value of SNR leads to better overall normalized throughput. The contribution of this paper is that increasing the noise uncertainty by 50% decreases throughput by 8%. On the other hand, noise uncertainty of 50% can be overcome if the sensing time reaches 2% of the total time. This work can be extended to include eigenvalue based detector.