Stationary Analysis of Geo/Geo/1 Queue with Two-Speed Service and the Optimal Switching Threshold for the Service Rate ()
1. Introduction
In the classical queueing literature, the server is usually assumed to work at constant speed as long as there is any work present. However, we know that this assumption may not always be appropriate when the system’s workload affects the server’s efficiency in some real world situations. To better understand this fact, we can cite some practical examples to illustrate this point. In a manufacturing system, the decision-maker is responsible for deciding the service speed of the production equipment according to the level of market demand. If the current production capacity is far from meeting market demand, high service rate will be activated to balance the requirements. Nonetheless, once the demand is satisfied and decreases significantly, production will be slowed down to avoid inventory pile up. In addition, the telephone-based directory assistance is another convincing example of service rate depending on the queue length, where as the number of calls increases, the provision of extra attendants is recommended so as to provide better quality of service in terms of reduced waiting time. However, these extra attendants may be removed when the peak time is over and the number of phone calls sharply reduces. Therefore, these real-life applications that mentioned above constitute the main motivation of our study.
Actually, there is a considerable body of queueing literature that deals with workload-dependent service rate. Among some early papers in this area are those by Satty [1] and Gebhard [2] , both of whom considered some fundamental queueing problems such as the stationary queue size distribution and the expected queue length for the M/M/1 queue. Their work spawned research into modeling a queueing system with adaptable service rate, such as by Gross and Harris [3] , Harris and Marchal [4] , William and Wang [5] , Bekker et al. [6] and Zhernovyi [7] . In the past several decades, an important extension to the above model is the multi-server queueing system with queue-dependent servers. Singh [8] respectively analyzed the infinite source M/M/2 queueing systems with two homogeneous and heterogeneous servers. A relationship among the system operating costs, traffic intensity and the queue size is obtained. Later, based on the Singh’s pioneering work, Garg and Singh [9] revisited the same system and established a cost structure to determine the optimal queue length at which the second server was provided, so that the system may gain the maximum profit. With the assumption that the system capacity was limited, Wang and Tai [10] studied queue-dependent servers in the finite buffer M/M/3 queue with three types of service rate. They constructed a relationship among the costs to determine the optimal queue lengths J and K of providing the second server and the third server, respectively. Furthermore, not long ago, Jain [11] investigated the finite capacity M/M/r queueing system with r heterogeneous servers. In particular, the optimal threshold parameters for turning on the servers were obtained in her work. More recently, M/M/r ueueing model with infinite capacity and queue-dependent servers was considered by Lin and Ke [12] . Using the genetic algorithm, they found the best thresholds of queue length in activating servers and their corresponding service rate. These studies greatly enhance the practical value of the multi-server queueing theory since it is realistic to consider the changes in the number of working servers.
However, we may note a common feature existing in the above research works, namely, authors invariably assum that whenever the number of customers or jobs in the system exceeds a certain threshold, the service rate is accelerated to deal with the lengthy queue. Further, if the queue length reduces to less than the threshold, lower service rate is resumed. In fact, such model assumption means that the service rate can be switched countlessly in a regeneration cycle. Here, for the single server queue, the regeneration cycle is the time span between two consecutive starting points of the server’s idle period. Obviously, whenever a server is switched from low service rate to high service rate, or vice-versa, switching cost is incurred. The more the server switches its service rate, the more additional cost it has to face. In other words, if the switch is reiterated over a long period of time, substantial amount of switching cost will be charged to the system. Therefore, the traditional service rate switching policy has some significant drawbacks in the queueing system with a relatively high arrival rate. In order to prevent switches from occurring too frequently, a modified service rate switching policy is proposed in this paper. Under the control of modified switching policy, the high service rate is activated as soon as L customers accumulate in the system and such service rate is preserved until the system becomes completely empty even if the number of customers falls below L. Hence, for the modified switching policy, the change of service rate can only occur at most once in a regeneration cycle. Undoubtedly, this policy will greatly reduce the switch- ing cost of the system. On the other hand, although a lot of continuous-time queueing models with workload- dependent service rate have been studied extensively in the past years, their discrete-time counterparts received very little attention in the literature. Except the studies done by Chaudhry [13] [14] and Parthasarathy and Lenin [15] , no work in this direction has come to our notice. Given that the wide applications of discrete-time queue in digital data networks and flexible manufacturing systems, in this paper, we will develop an analytical model that allows us to extensively analyze and explore the Markovian queueing system with workload-dependent service rate in discrete-time case. Through our work, we wish to develop a computational model that helps decision- makers answer the following important questions: 1) Under a certain cost structure, what is the optimal value of L that minimizes the long-runaverage cost rate function? 2) If the system state information is communicated to the customers upon their arrival, how to evaluate the expected conditional sojourn time of an arriving customer?
The rest of this paper is organized as follows. In Section 2, we describe the mathematical model for the problem under consideration. The steady-state analysis of the model is presented in Section 3 and some important system performance measures are derived in this section. Using the first-step argument, we develop an analytical scheme for the customer’s sojourn time. Furthermore, we also carried out regeneration cycle analysis to find the expected length of two types of busy periods. In Section 4, a long-run average cost rate function is established based on the system characteristics to determine the optimal switching threshold for the service rate. Section 5 concludes the research and suggests some future topics.
2. Model Formulation
We consider a discrete-time queue with single server or machine, whose service rate may be affected by the number of customers or jobs present in the system. In our model, inter-arrival times 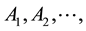 are independent and identically distributed (i.i.d.) random variables with probability mass function (p.m.f.)
are independent and identically distributed (i.i.d.) random variables with probability mass function (p.m.f.) 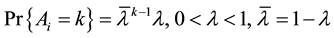 and
and . Arriving customers form a single waiting line based on the order of their arrival. Initially, when the number of customers in the system is less than the given threshold level
. Arriving customers form a single waiting line based on the order of their arrival. Initially, when the number of customers in the system is less than the given threshold level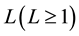 , the server serves customers with low service rate. The high service rate is activated at the instant when the number of customers in the system becomes equal to L, and it will be preserved until the long queue empties. Here, we assume that the two types of service times, namely
, the server serves customers with low service rate. The high service rate is activated at the instant when the number of customers in the system becomes equal to L, and it will be preserved until the long queue empties. Here, we assume that the two types of service times, namely  and
and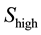 , are independent and geometrically distributed with respective p.m.fs
, are independent and geometrically distributed with respective p.m.fs
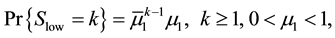

where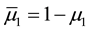 ,
, 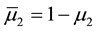 and
and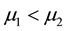 .
. ,
,  and
and 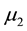 denote the customer arrival rate, low service rate and high service rate, respectively.
denote the customer arrival rate, low service rate and high service rate, respectively.
In discrete-time queueing system, the time axis is divided into equal intervals called slots and all queueing activities occur at the slot boundaries. Traditionally, there are two types of systems in the discrete-time case (see [16] and [17] ), one is the late arrival with delayed access (LAS-DA) and the other is the early arrival system (EAS). In this paper, we consider the model for the late arrival system with delayed access and therefore, a potential arrival occurs in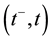 , and a potential departure takes place in
, and a potential departure takes place in , for
, for![]() . To make it clear, the various time epochs at which events occur are shown in a self-explanatory figure (see Figure 1).
. To make it clear, the various time epochs at which events occur are shown in a self-explanatory figure (see Figure 1).
3. Steady-State Analysis
In this section, we first apply the Markov process theory to obtain the steady-state difference equations governing the system. Next, the generating function technique and a recursive method are employed to develop the analytical solutions in a neat close-form. Toward this end, we need to define some commonly used notations to analyze the queueing system as follows:
![]() the number of customers in the system at time
the number of customers in the system at time![]() ,
,
![]() the server speed state at time
the server speed state at time![]() ,
,
where
![]()
Figure 1. Various time epochs in late arrival system with delayed access (LAS-DA).
![]()
Therefore, ![]() is the Markov chain for queueing system with state space
is the Markov chain for queueing system with state space
![]()
Furthermore, let us define the following stationary probability distributions for the Markov chain:
![]()
![]()
3.1. Steady-State Equation
From the state-transition-rate diagram for the Geo/Geo/1 queue with service rate switching threshold (see Figure 2), we can set up steady-state equations for ![]() and
and ![]() in the following:
in the following:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Remark 1. The Markov chain ![]() is called stable if it is irreducible and all states are ergodic. As illustrated in Figure 2, the state space of this queueing system is a single communicating class. Thus, the Markov chain
is called stable if it is irreducible and all states are ergodic. As illustrated in Figure 2, the state space of this queueing system is a single communicating class. Thus, the Markov chain ![]() is irreducible. Under assumption that
is irreducible. Under assumption that![]() , it is clear from the standard Geo/Geo/1 theory that
, it is clear from the standard Geo/Geo/1 theory that ![]() is a necessary and sufficient condition for ergodicity of the system. Intuitively speaking, if, on average, arrivals happen faster than service completions the queue will grow indefinitely long and the system will not have a stationary distribution.
is a necessary and sufficient condition for ergodicity of the system. Intuitively speaking, if, on average, arrivals happen faster than service completions the queue will grow indefinitely long and the system will not have a stationary distribution.
Remark 2. Relating the state probabilities at epochs t and ![]() or
or ![]() and
and![]() , and letting
, and letting![]() , we can easily obtain a set of difference equations, which have exactly the same mathematical form as Equations (1)-(8). So the stationary probabilities of the system state at epochs t and
, we can easily obtain a set of difference equations, which have exactly the same mathematical form as Equations (1)-(8). So the stationary probabilities of the system state at epochs t and ![]() are identical with the one at epoch
are identical with the one at epoch
![]()
Figure 2. State-transition-rate diagram for the Geo/Geo/1 queue with switching threshold for service rate.
![]() . Furthermore, in LAS-DA, since an outside observer’s observation epoch falls in a time interval after a potential departure and before a potential arrival, the probability that outside observer sees i customers in the system and the server in state j is also the same as
. Furthermore, in LAS-DA, since an outside observer’s observation epoch falls in a time interval after a potential departure and before a potential arrival, the probability that outside observer sees i customers in the system and the server in state j is also the same as![]() . For these reasons, only the system state probability at time point
. For these reasons, only the system state probability at time point ![]() is considered in this paper.
is considered in this paper.
3.2. Two Relationships between P0,0 and PL−1,0
In this subsection, we first derive two important relationships between ![]() and
and![]() . On this basis, we also give the explicit expression for the stationary probability
. On this basis, we also give the explicit expression for the stationary probability![]() . In later section, we will see that this quantity is very useful when the cost structure will be introduced in our model. To this end, let us first define the following probability generating functions:
. In later section, we will see that this quantity is very useful when the cost structure will be introduced in our model. To this end, let us first define the following probability generating functions:
![]()
![]()
Multiplying Equations (1)-(4) by ![]() and summing over n,
and summing over n, ![]() , we obtain
, we obtain
![]() (9)
(9)
If we add the right hand sides and left hand sides of the Equations (1)-(4) and cancel the common terms, the following equality holds:
![]() (10)
(10)
Remark 3. As shown in Figure 2, according to the different service rates provided by the server, the state space of the queueing system is divided into two macro-states, namely 0 and 1. They are accessible to each other. Thus, the mean transition rate from state ![]() to state
to state ![]() is equal to the mean rate from state (1,1) to state (0,0). This fact is properly reflected in the above Equation (10).
is equal to the mean rate from state (1,1) to state (0,0). This fact is properly reflected in the above Equation (10).
Substituting Equation (10) into Equation (9) and after some algebraic manipulation, we have
![]() (11)
(11)
Using a method similar to the derivation of Equation (11), with Equations (5)-(8), we get
![]() (12)
(12)
Thus, we can rewrite ![]() as follows:
as follows:
![]() (13)
(13)
Since ![]() is the probability generating function of the queue length distribution, we have
is the probability generating function of the queue length distribution, we have![]() . By taking into account the normalization condition, and letting
. By taking into account the normalization condition, and letting ![]() in Equation (13), we have
in Equation (13), we have
![]() (14)
(14)
Based on Equation (14) the first relationship between ![]() and
and ![]() is given by
is given by
![]() (15)
(15)
On the other hand, with the help of Equations (2)-(4), another relationship between ![]() and
and ![]() can be obtained by a backward recursion procedure.
can be obtained by a backward recursion procedure.
![]() (16)
(16)
Substituting Equation (16) into Equation (15), it follows that:
![]() (17)
(17)
Remark 4. Obviously, the queueing system for ![]() coincides with the classic Geo/Geo/1 queue studied by Hunter [16] . Additionally, under such an assumption, after some brief algebraic manipulations, the Equation
coincides with the classic Geo/Geo/1 queue studied by Hunter [16] . Additionally, under such an assumption, after some brief algebraic manipulations, the Equation
(17) can further be simplified as follows:![]() , where
, where![]() . The formula derived here agrees with
. The formula derived here agrees with
the one given by Hunter [16] , and it also shows the correctness of our analysis presented above.
Having computed the stationary probabilities ![]() and
and![]() , a recursive algorithm for computing the other steady state probabilities can be established. To demonstrate the working schemes of the recursive method, we describe the solution algorithm in the following Table 1.
, a recursive algorithm for computing the other steady state probabilities can be established. To demonstrate the working schemes of the recursive method, we describe the solution algorithm in the following Table 1.
3.3. Explicit Expression for the Expected Number of Customers in the System
Once the explicit expressions for ![]() and
and ![]() are given, the expected number of customers in the system can be determined from them. Let N be the number of customers in the system in steady state. We have
are given, the expected number of customers in the system can be determined from them. Let N be the number of customers in the system in steady state. We have
![]()
Table 1. Comutation of the stationary distribution![]() .
.
![]()
Using L’Hospital’s Rule twice while taking limits![]() , we get
, we get
![]() (18)
(18)
Remark 5. As a matter of fact, the explicit expression for the expected number of customers in the system has been given by Equation (18). Just because the explicit expressions ![]() and
and ![]() are slightly cumbersome to write, we do not indent to substitute Equations (16) and (17) into Equation (18).
are slightly cumbersome to write, we do not indent to substitute Equations (16) and (17) into Equation (18).
3.4. Sojourn Time Performance
In this subsection, we deal with the customer’s sojourn time W, defined as the time between the arrival epoch of a customer till the instant at which his service request is satisfied. Here, our aim is to determine the first order moment of the sojourn time. To achieve this goal, we need to introduce some auxiliary random variables.
![]() : Customer’s sojourn time given that he finds the queueing system at state
: Customer’s sojourn time given that he finds the queueing system at state ![]() just before his arrival and the residual service time of customer that the server is currently processing is greater than or equal to one time slot.
just before his arrival and the residual service time of customer that the server is currently processing is greater than or equal to one time slot. ![]()
![]() : Conditional sojourn time of a customer who arrives at the system when its state is
: Conditional sojourn time of a customer who arrives at the system when its state is![]() .
.![]()
We also denote the corresponding z-transforms of W, ![]() and
and ![]() by
by![]() ,
, ![]() and
and ![]() re- spectively. Furthermore, because of the BASTA (i.e. Bernoulli arrivals see time averages) property, we have that
re- spectively. Furthermore, because of the BASTA (i.e. Bernoulli arrivals see time averages) property, we have that
![]() (19)
(19)
By differentiating Equation (19) with respect to z, and evaluating at![]() , we arrive at
, we arrive at
![]() (20)
(20)
For determining the unknowns ![]() and
and![]() , we apply a first-step argument and set up the following equations.
, we apply a first-step argument and set up the following equations.
![]() (21)
(21)
Assume that a customer arrival will occur in![]() . If prior to this arrival there are
. If prior to this arrival there are ![]() customers in the system and the server is busy with low service rate, then the departure of the customer that the server is currently processing will take place in
customers in the system and the server is busy with low service rate, then the departure of the customer that the server is currently processing will take place in ![]() with probability
with probability![]() , thus
, thus ![]() is the probability that the above event does not occur. Hence we can easily get the following relationships
is the probability that the above event does not occur. Hence we can easily get the following relationships
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
For the same reason as mentioned above, when a customer arrives at the system during a busy period with high service rate, we conclude that ![]() satisfies
satisfies
![]() (25)
(25)
Alternatively, we can use the memoryless property of the geometric distribution to find the z-transform of![]() . For
. For![]() ,
,
![]() (26)
(26)
For![]() , we have
, we have
![]() (27)
(27)
Similarly, for ![]() and
and![]() , we have
, we have
![]() (28)
(28)
Differentiating both sides of Equation (21) and Equations (25)-(28) with respect to z and evaluating at![]() , we can obtain the following equations for the first moment of the conditional sojourn time.
, we can obtain the following equations for the first moment of the conditional sojourn time.
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
Therefore, from the above results and Equations (22)-(24), we obtain
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
Thus, the problem of computing the mean conditional sojourn times ![]() and
and ![]() can be considered solved. Consequently, with the help of stationary probability
can be considered solved. Consequently, with the help of stationary probability![]() , we can evaluate the expectation of the unconditional sojourn time by using Equation (20).
, we can evaluate the expectation of the unconditional sojourn time by using Equation (20).
To demonstrate the feasibility and efficiency of the proposed algorithm, a numerical experiment is carried out on a personal computer implementing an Intel Core i5 CPU (2.7 GHz) and 4.0 GB RAM. In this example, we select![]() ,
, ![]() ,
, ![]() and let
and let ![]() vary from 0.1 to 0.16. Figure 3 illustrates the effect of customer’s arrival rate on the mean value of the unconditional sojourn time. Also, on putting
vary from 0.1 to 0.16. Figure 3 illustrates the effect of customer’s arrival rate on the mean value of the unconditional sojourn time. Also, on putting![]() , the queueing system under consideration can be regarded as the classic Geo/Geo/1 queue with constant service rate. From Figure 3 we can conclude that setting the switching threshold for the service rate can greatly reduce the customer’s average sojourn time, for example, when the customer arrival rate is 0.16, the gap between the two average sojourn times is about 25 time units.
, the queueing system under consideration can be regarded as the classic Geo/Geo/1 queue with constant service rate. From Figure 3 we can conclude that setting the switching threshold for the service rate can greatly reduce the customer’s average sojourn time, for example, when the customer arrival rate is 0.16, the gap between the two average sojourn times is about 25 time units.
3.5. Regeneration Cycle
Regeneration cycles are models of stochastic phenomena in which an event (or combination of events) occurs repeatedly over time, and the times between occurrences are independent and identically distributed. Models of such phenomena typically focus on determining limiting averages for costs or other system parameters. In this paper, the reason for performing regeneration cycle analysis is to determine the optimal switching threshold value L, where the high service rate is activated.
A regeneration cycle of our current model consists of a server’s idle period and a server’s busy period. As regeneration points, we choose the points at which the system becomes empty. There are two types of cycles depending on whether there is a change in service rate during the server’s busy period. A cycle is called “type-1” if it does not include switching of the service rate; otherwise it is of “type-2” cycle. To better understand the struc- ture of regeneration cycle, examples of the type-1 and type-2 cycles are shown in Figure 4 and Figure 5, respectively.
We denote ![]() as the probability generating function of the busy period for classical Geo/Geo/1 queue. If customer arrival occurs according to a Bernoulli process with parameter
as the probability generating function of the busy period for classical Geo/Geo/1 queue. If customer arrival occurs according to a Bernoulli process with parameter![]() , and the service times provided by a
, and the service times provided by a
![]()
Figure 3. The effect of λ on the mean value of the unconditional sojourn time.
![]()
Figure 4. An example of the type-1 cycle.
![]()
Figure 5. An example of the type-2 cycle.
single server follow geometric distribution with parameter![]() , then from Takagi [17] , we have
, then from Takagi [17] , we have
![]()
![]()
where ![]() is the mean value of the busy period for classic Geo/Geo/1 queue. Furthermore, let I,
is the mean value of the busy period for classic Geo/Geo/1 queue. Furthermore, let I, ![]() and
and ![]() respectively denote the length of server’s idle period and the length of busy periods with low and high service rates in a regeneration cycle. It is obvious that I follows geometric distribution, thus
respectively denote the length of server’s idle period and the length of busy periods with low and high service rates in a regeneration cycle. It is obvious that I follows geometric distribution, thus![]() . Next, we derive the probability generating function of busy period with high service rate
. Next, we derive the probability generating function of busy period with high service rate![]() . According to the model assumptions, the busy period with high service rate is only activated by L customers waiting in the queue (including the one in service). By conditioning on the duration of the remaining service time for the customer currently being served, we get
. According to the model assumptions, the busy period with high service rate is only activated by L customers waiting in the queue (including the one in service). By conditioning on the duration of the remaining service time for the customer currently being served, we get
![]() (37)
(37)
where ![]() denotes the probability that the service rate does switch in a regeneration cycle. Thus, from Equation (37), we have
denotes the probability that the service rate does switch in a regeneration cycle. Thus, from Equation (37), we have
![]() (38)
(38)
On the other hand, let ![]() be the unconditional expected length of the regeneration cycle, the mean duration of busy period with high service rate can also be obtained from a result of renewal theory. Using
be the unconditional expected length of the regeneration cycle, the mean duration of busy period with high service rate can also be obtained from a result of renewal theory. Using
![]()
![]()
![]()
we can get
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
Comparing the right hand sides of Equations (38) and (41), we see that
![]()
Once we have found the expressions of![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , we can try to construct the cost structure of this queueing system in the next section.
, we can try to construct the cost structure of this queueing system in the next section.
4. Optimal Switching Threshold for the Service Rate and Numerical Examples
In manufacturing process management, managers are always interested in minimizing the long-run average cost per unit time of the system. In this section, based on the performance measures that we obtained in the previous section and the renewal reward theorem, we first construct an expected cost rate function ![]() for the Geo/Geo/1 queue with switching threshold for the service rate, in which a key decision variable L is considered. Here, our objective is to determine the optimal threshold value
for the Geo/Geo/1 queue with switching threshold for the service rate, in which a key decision variable L is considered. Here, our objective is to determine the optimal threshold value ![]() under some cost structure, so as to minimize the long-run average cost rate.
under some cost structure, so as to minimize the long-run average cost rate.
Let us consider the following cost elements:
![]() setup cost per cycle;
setup cost per cycle;
![]() switching cost for changing the service rate in a regeneration cycle;
switching cost for changing the service rate in a regeneration cycle;
![]() holding cost per customer per unit time;
holding cost per customer per unit time;
![]() running cost per unit time when the service provides low speed service;
running cost per unit time when the service provides low speed service;
![]() running cost per unit time when the service provides high speed service.
running cost per unit time when the service provides high speed service.
Utilizing the definition of each cost element listed above, the long-run average cost rate minimization problem can be illustrated mathematically as
![]()
As shown in Figure 4 and Figure 5, the switching cost is incurred at most only once in a regeneration cycle, and the switching occurs with probability![]() . This is the reason why we multiply
. This is the reason why we multiply ![]() by
by ![]() in our cost structure. On the other hand, we also note that it is rather difficult to develop analytic results for the optimal value of L because the long-run average cost rate function is highly non-linear and complex. In spite of that, since L is a discrete variable, the optimal value
in our cost structure. On the other hand, we also note that it is rather difficult to develop analytic results for the optimal value of L because the long-run average cost rate function is highly non-linear and complex. In spite of that, since L is a discrete variable, the optimal value ![]() may be found by using direct substitution of successive values of L into the long-run average cost rate function until the minimum value
may be found by using direct substitution of successive values of L into the long-run average cost rate function until the minimum value ![]() is achieved.
is achieved.
To illustrate the direct search algorithm described above, a numerical example is provided by considering the following cost parameters:
![]()
and other system parameters are taken as![]() ,
, ![]() ,
,![]() . Substituting these values into
. Substituting these values into![]() , we can obtain the results presented in Table 2 and Figure 6. The curve representing the long-run average cost rate function
, we can obtain the results presented in Table 2 and Figure 6. The curve representing the long-run average cost rate function ![]() is plotted in Figure 6 for different values of L. As can be seen in Figure 6, we observe that this function is convex and a single relative minimum exists. The optimal value
is plotted in Figure 6 for different values of L. As can be seen in Figure 6, we observe that this function is convex and a single relative minimum exists. The optimal value ![]() and the corresponding long-run average cost rate
and the corresponding long-run average cost rate ![]() are tabulated in Table 2. From Table 2, it appears that the minimum average cost per unit time of 24.2347 is obtained with
are tabulated in Table 2. From Table 2, it appears that the minimum average cost per unit time of 24.2347 is obtained with![]() .
.
5. Conclusion
In this paper, we have carried out an analysis of a discrete-time infinite-buffer Geo/Geo/1 queuing system under
![]()
Table 2. The long-run average cost rate against the values of L.
![]()
Figure 6. The plot of TC(L) against the switching threshold L.
a modified service rate switching policy that has potential applications in modeling manufacturing and telecommunication systems. We have developed a recursive method to find the steady-state queue size distribution. The recursive method is powerful and easy to implement. Further, we obtain the analytically explicit expressions for the expected number of customers in the system. Using the first-step argument, a simple algorithm for calculating the customer’s mean sojourn time has been proposed. Moreover, we also performed regeneration cycle analysis of the queue to find the optimal service rate switching threshold L. Our current model is useful and significant to engineers or managers who design an efficient system with economic management. It should be pointed out that the economic importance of this model resides in the multiple applications to manufacturing processes, since most of them operate on a discrete time basis. Furthermore, the optimal control of service rate switching policy is also a main objective from the enterprise point of view. For future studies, the present investigation can be extended by incorporating bulk input or bulk service. Another area of interest may be expanding our model into Geo/G/1 type, because there will be a significant improvement inapplicability to real world system.
Acknowledgements
The work described in this paper is supported by Sichuan Provincial Department of Education (14ZB0221).